Generate Parentheses

标签：

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

For example, given n = 3, a solution set is:

"((()))", "(()())", "(())()", "()(())", "()()()"

问题分析：

给出数字n，求出所有合法的表达式。

我们用二叉树形象的表示这种关系。然后再把二叉树转化为代码的形式。因为二叉树的定义就是递归定义的，因此本题很明显应该使用递归的形式。

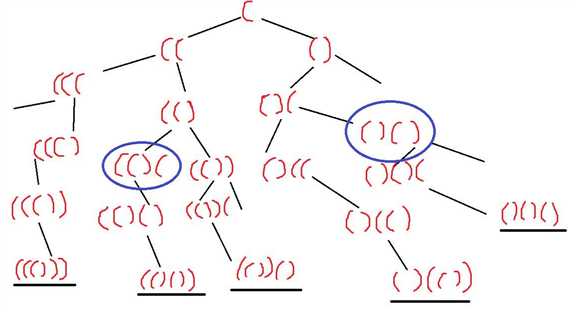
从上面的图片中我们可以很明显的看到，最后五条画黑线的就是最终的结果，其中左分支都是添加左括号，又分支都是添加右括号。

这道题其实是关于卡特兰数的，如果只是要输出结果有多少组，那么直接用卡特兰数的公式就可以。

方法：

一般来说是用递归的方法，因为可以归结为子问题去操作。在每次递归函数中记录左括号和右括号的剩余数量，然后有两种选择，一个是放一个左括号，另一种是放一个右括号。当然有一些否定条件，比如剩余的右括号不能比左括号少，或者左括号右括号数量都要大于0。正常结束条件是左右括号数量都为0。算法的复杂度是O(结果的数量)，因为卡特兰数并不是一个多项式量级的数字，所以算法也不是多项式复杂度的。

代码：

    vector<string> generateParenthesis(int n) {
        vector<string> ret;
        helper(ret, n, n, "");
        return ret;
    }

    void helper(vector<string> &ret, int l, int r, string str)
    {
        if (l>r)
        {
            return;
        }

        if (l==0 && r==0)
        {
            ret.push_back(str);
        }

        if (l>0)
        {
            helper(ret, l-1, r, str+‘(‘);
        }
        if (r>0)
        {
            helper(ret, l, r-1, str+‘)‘);
        }
    }

参考：

1. http://www.shangxueba.com/jingyan/1837405.html [卡特兰数问题]

2. http://blog.csdn.net/linhuanmars/article/details/19873463

Generate Parentheses

标签：

原文地址：http://www.cnblogs.com/jellyang/p/4353760.html