标签:codeforces
比赛链接:http://codeforces.com/contest/527
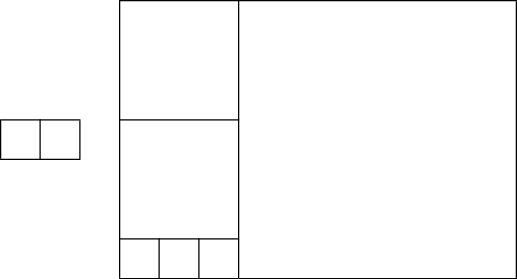
One day Vasya was sitting on a not so interesting Maths lesson and making an origami from a rectangular a mm ?×? b mm sheet of paper (a?>?b). Usually the first step in making an origami is making a square piece of paper from the rectangular sheet by folding the sheet along the bisector of the right angle, and cutting the excess part.
After making a paper ship from the square piece, Vasya looked on the remaining (a?-?b) mm ?×? b mm strip of paper. He got the idea to use this strip of paper in the same way to make an origami, and then use the remainder (if it exists) and so on. At the moment when he is left with a square piece of paper, he will make the last ship from it and stop.
Can you determine how many ships Vasya will make during the lesson?
The first line of the input contains two integers a, b (1?≤?b?<?a?≤?1012) — the sizes of the original sheet of paper.
Print a single integer — the number of ships that Vasya will make.
2 1
2
10 7
6
1000000000000 1
1000000000000
Pictures to the first and second sample test.
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
int main()
{
ll a, b, ans = 0;
cin >> a >> b;
ll tmp = a % b;
if(tmp == 0)
{
cout << a / b << endl;
return 0;
}
else
{
ans += a / b;
a = max(tmp, b);
b = tmp + b - a;
}
while(a % b)
{
tmp = a - b;
a = max(b, tmp);
b = b + tmp - a;
ans++;
}
cout << ans + (a / b)<< endl;
}
Ford Prefect got a job as a web developer for a small company that makes towels. His current work task is to create a search engine for the website of the company. During the development process, he needs to write a subroutine for comparing strings S and T of equal length to be "similar". After a brief search on the Internet, he learned about the Hamming distance between two strings S and T of the same length, which is defined as the number of positions in which S and T have different characters. For example, the Hamming distance between words "permanent" and "pergament" is two, as these words differ in the fourth and sixth letters.
Moreover, as he was searching for information, he also noticed that modern search engines have powerful mechanisms to correct errors in the request to improve the quality of search. Ford doesn‘t know much about human beings, so he assumed that the most common mistake in a request is swapping two arbitrary letters of the string (not necessarily adjacent). Now he wants to write a function that determines which two letters should be swapped in string S, so that the Hamming distance between a new string S and string T would be as small as possible, or otherwise, determine that such a replacement cannot reduce the distance between the strings.
Help him do this!
The first line contains integer n (1?≤?n?≤?200?000) — the length of strings S and T.
The second line contains string S.
The third line contains string T.
Each of the lines only contains lowercase Latin letters.
In the first line, print number x — the minimum possible Hamming distance between strings S and T if you swap at most one pair of letters in S.
In the second line, either print the indexes i and j (1?≤?i,?j?≤?n, i?≠?j), if reaching the minimum possible distance is possible by swapping letters on positions i and j, or print "-1 -1", if it is not necessary to swap characters.
If there are multiple possible answers, print any of them.
9
pergament
permanent
1
4 6
6
wookie
cookie
1
-1 -1
4
petr
egor
2
1 2
6
double
bundle
2
4 1
In the second test it is acceptable to print i?=?2, j?=?3.
题目大意:给两个长度相同的字符串,它们的距离定义为对应位置上字符不同的个数,现在问第二个字符串可以任意交换两个字符,若可以减少它们的距离则输出尽可能多的减少距离的方案的字符下标,否则输出-1 -1
题目分析:把不同的筛出来,map搞一搞,模拟一下
#include <cstdio>
#include <iostream>
#include <string>
#include <map>
using namespace std;
int const MAX = 200001;
int re[MAX];
map <char, int> mp;
int main()
{
string a, b, a1, b1;
mp.clear();
int n, len = 0, pos1, pos2;
scanf("%d", &n);
cin >> a >> b;
for(int i = 0; i < n; i++)
{
if(a[i] != b[i])
{
re[len ++] = i + 1;
b1 += b[i];
a1 += a[i];
}
}
for(int i = 0; i < len; i++)
if(!mp[a1[i]])
mp[a1[i]] = i;
if(len == 0 || len == 1)
{
printf("%d\n-1 -1\n", len);
return 0;
}
bool flag = false, flag2 = false;
map <char ,int> :: iterator it = mp.begin();
for(int i = 0; i < len; i++)
{
it = mp.find(b1[i]);
if(it != mp.end())
{
flag2 = true;
pos1 = re[i];
pos2 = re[it -> second];
if(b1[it -> second] == a1[i])
{
pos2 = re[it -> second];
flag = true;
break;
}
}
}
if(!flag2)
{
printf("%d\n-1 -1\n", len);
return 0;
}
if(flag)
{
printf("%d\n%d %d\n", len - 2, pos1, pos2);
return 0;
}
else
{
printf("%d\n%d %d\n", len - 1, pos1, pos2);
return 0;
}
}
Leonid wants to become a glass carver (the person who creates beautiful artworks by cutting the glass). He already has a rectangular w mm ?×? h mm sheet of glass, a diamond glass cutter and lots of enthusiasm. What he lacks is understanding of what to carve and how.
In order not to waste time, he decided to practice the technique of carving. To do this, he makes vertical and horizontal cuts through the entire sheet. This process results in making smaller rectangular fragments of glass. Leonid does not move the newly made glass fragments. In particular, a cut divides each fragment of glass that it goes through into smaller fragments.
After each cut Leonid tries to determine what area the largest of the currently available glass fragments has. Since there appear more and more fragments, this question takes him more and more time and distracts him from the fascinating process.
Leonid offers to divide the labor — he will cut glass, and you will calculate the area of the maximum fragment after each cut. Do you agree?
The first line contains three integers w,?h,?n (2?≤?w,?h?≤?200?000, 1?≤?n?≤?200?000).
Next n lines contain the descriptions of the cuts. Each description has the form H y or V x. In the first case Leonid makes the horizontal cut at the distance y millimeters (1?≤?y?≤?h?-?1) from the lower edge of the original sheet of glass. In the second case Leonid makes a vertical cut at distance x (1?≤?x?≤?w?-?1) millimeters from the left edge of the original sheet of glass. It is guaranteed that Leonid won‘t make two identical cuts.
After each cut print on a single line the area of the maximum available glass fragment in mm2.
4 3 4 H 2 V 2 V 3 V 1
8 4 4 2
7 6 5 H 4 V 3 V 5 H 2 V 1
28 16 12 6 4
Picture for the first sample test:


题目大意:一块高h宽w的玻璃,现在要切n刀,H y表示在纵坐标y处水平切一刀,V x表示在横坐标x处竖直切一刀,每切一刀,输出当前最大的玻璃块的面积
题目分析:stl的应用,4个multiset,分别代表横着切的位置,竖着切的位置,横着的边长,竖着的边长,然后就切一切,插一插,搞一搞,multiset自带排序,每次取横竖的最后一个值相乘,就是当前的最大面积
#include <cstdio>
#include <iostream>
#include <set>
#define ll long long
using namespace std;
int w, h, n;
multiset <int> wpos, hpos, wlen, hlen;
multiset <int> :: iterator it, it1, it2;
int main()
{
char s[2];
int pos;
scanf("%d %d %d", &w, &h, &n);
wpos.insert(0);
wpos.insert(w);
hpos.insert(0);
hpos.insert(h);
wlen.insert(w);
hlen.insert(h);
while(n --)
{
scanf("%s %d", s, &pos);
if(s[0] == 'H')
{
hpos.insert(pos);
it = hpos.find(pos);
it1 = it2 = it;
it1 --;
it2 ++;
hlen.erase(hlen.find(*it2 - *it1));
hlen.insert(*it2 - *it);
hlen.insert(*it - *it1);
}
else
{
wpos.insert(pos);
it = wpos.find(pos);
it1 = it2 = it;
it1 --;
it2 ++;
wlen.erase(wlen.find(*it2 - *it1));
wlen.insert(*it2 - *it);
wlen.insert(*it - *it1);
}
it1 = wlen.end();
it2 = hlen.end();
ll a = *(--it1);
ll b = *(--it2);
cout << a * b * 1ll << endl;
}
}
The clique problem is one of the most well-known NP-complete problems. Under some simplification it can be formulated as follows. Consider an undirected graph G. It is required to find a subset of vertices C of the maximum size such that any two of them are connected by an edge in graph G. Sounds simple, doesn‘t it? Nobody yet knows an algorithm that finds a solution to this problem in polynomial time of the size of the graph. However, as with many other NP-complete problems, the clique problem is easier if you consider a specific type of a graph.
Consider n distinct points on a line. Let the i-th point have the coordinate xi and weight wi. Let‘s form graph G, whose vertices are these points and edges connect exactly the pairs of points (i,?j), such that the distance between them is not less than the sum of their weights, or more formally: |xi?-?xj|?≥?wi?+?wj.
Find the size of the maximum clique in such graph.
The first line contains the integer n (1?≤?n?≤?200?000) — the number of points.
Each of the next n lines contains two numbers xi, wi (0?≤?xi?≤?109,?1?≤?wi?≤?109) — the coordinate and the weight of a point. All xi are different.
Print a single number — the number of vertexes in the maximum clique of the given graph.
4 2 3 3 1 6 1 0 2
3
If you happen to know how to solve this problem without using the specific properties of the graph formulated in the problem statement, then you are able to get a prize of one million dollars!
The picture for the sample test.

#include <cstdio>
#include <algorithm>
using namespace std;
int const MAX = 200005;
int const INF = 0x3fffffff;
struct Point
{
int fir, sec;
}p[MAX];
int cmp(Point a , Point b)
{
return a.sec < b.sec;
}
int main()
{
int n, x, w;
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
scanf("%d %d", &x, &w);
p[i].fir = x - w;
p[i].sec = x + w;
}
sort(p, p + n,cmp);
int ma = -INF, ans = 0;
for(int i = 0; i < n; i++)
{
if(p[i].fir >= ma)
{
ans ++;
ma = p[i].sec;
}
}
printf("%d\n", ans);
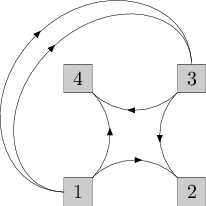
}The project of a data center of a Big Software Company consists of n computers connected by m cables. Simply speaking, each computer can be considered as a box with multiple cables going out of the box. Very Important Information is transmitted along each cable in one of the two directions. As the data center plan is not yet approved, it wasn‘t determined yet in which direction information will go along each cable. The cables are put so that each computer is connected with each one, perhaps through some other computers.
The person in charge of the cleaning the data center will be Claudia Ivanova, the janitor. She loves to tie cables into bundles using cable ties. For some reasons, she groups the cables sticking out of a computer into groups of two, and if it isn‘t possible, then she gets furious and attacks the computer with the water from the bucket.
It should also be noted that due to the specific physical characteristics of the Very Important Information, it is strictly forbidden to connect in one bundle two cables where information flows in different directions.
The management of the data center wants to determine how to send information along each cable so that Claudia Ivanova is able to group all the cables coming out of each computer into groups of two, observing the condition above. Since it may not be possible with the existing connections plan, you are allowed to add the minimum possible number of cables to the scheme, and then you need to determine the direction of the information flow for each cable (yes, sometimes data centers are designed based on the janitors‘ convenience...)
The first line contains two numbers, n and m (1?≤?n?≤?100?000, 1?≤?m?≤?200?000) — the number of computers and the number of the already present cables, respectively.
Each of the next lines contains two numbers ai,?bi (1?≤?ai,?bi?≤?n) — the indices of the computers connected by the i-th cable. The data centers often have a very complex structure, so a pair of computers may have more than one pair of cables between them and some cables may connect a computer with itself.
In the first line print a single number p (p?≥?m) — the minimum number of cables in the final scheme.
In each of the next p lines print a pair of numbers ci,?di (1?≤?ci,?di?≤?n), describing another cable. Such entry means that information will go along a certain cable in direction from ci to di.
Among the cables you printed there should be all the cables presented in the original plan in some of two possible directions. It is guaranteed that there is a solution where p doesn‘t exceed 500?000.
If there are several posible solutions with minimum possible value of p, print any of them.
4 6 1 2 2 3 3 4 4 1 1 3 1 3
6 1 2 3 4 1 4 3 2 1 3 1 3
3 4 1 2 2 3 1 1 3 3
6 2 1 2 3 1 1 3 3 3 1 1 1
Picture for the first sample test. The tied pairs of cables are shown going out from the same point.
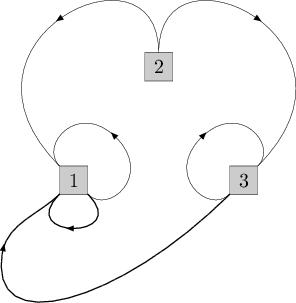
Picture for the second test from the statement. The added cables are drawin in bold.
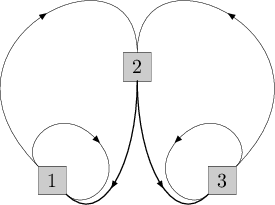
Alternative answer for the second sample test:
#include <cstdio>
#include <set>
using namespace std;
int const MAX = 1e6 + 5;
int n, m, cnt, tot, all;
int outd[MAX], a[MAX], ans[MAX];
multiset <int> e[MAX];
void DFS(int x)
{
while(!e[x].empty())
{
int i = *(e[x].begin());
e[x].erase(e[x].begin());
e[i].erase(e[i].find(x));
DFS(i);
}
ans[++ all] = x;
printf("%d\n", x);
}
int main()
{
int x, y;
scanf("%d %d", &n, &m);
while(m --)
{
scanf("%d %d", &x, &y);
e[x].insert(y);
e[y].insert(x);
outd[x] ++;
outd[y] ++;
cnt ++;
}
for(int i = 1;i <= n; i++)
if(outd[i] % 2)
a[++ tot] = i;
for(int i = 1; i < tot; i += 2)
{
e[a[i]].insert(a[i + 1]);
e[a[i + 1]].insert(a[i]);
cnt ++;
}
if(cnt % 2)
cnt ++;
printf("%d\n", cnt);
all = 0;
DFS(1);
for(int i = 1; i < all; i++)
{
if(i % 2)
printf("%d %d\n", ans[i], ans[i + 1]);
else
printf("%d %d\n", ans[i + 1], ans[i]);
}
if(!(all % 2))
printf("1 1\n");
}Codeforces Round #296 (Div. 2) (ABCDE题解)
标签:codeforces
原文地址:http://blog.csdn.net/tc_to_top/article/details/44524469