标签:
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 9479 | Accepted: 2168 |
Description
Mr.Dog was fired by his company. In order to support his family, he must find a new job as soon as possible. Nowadays, It‘s hard to have a job, since there are swelling numbers of the unemployed. So some companies often use hard tests for their recruitment.
The test is like this: starting from a source-city, you may pass through some directed roads to reach another city. Each time you reach a city, you can earn some profit or pay some fee, Let this process continue until you reach a target-city. The boss will compute the expense you spent for your trip and the profit you have just obtained. Finally, he will decide whether you can be hired.
In order to get the job, Mr.Dog managed to obtain the knowledge of the net profit Vi of all cities he may reach (a negative Vi indicates that money is spent rather than gained) and the connection between cities. A city with no roads leading to it is a source-city and a city with no roads leading to other cities is a target-city. The mission of Mr.Dog is to start from a source-city and choose a route leading to a target-city through which he can get the maximum profit.
Input
Output
Sample Input
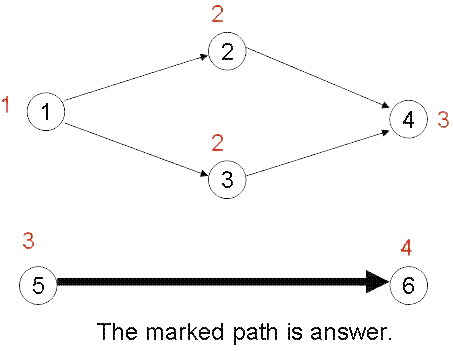
6 5 1 2 2 3 3 4 1 2 1 3 2 4 3 4 5 6
Sample Output
7
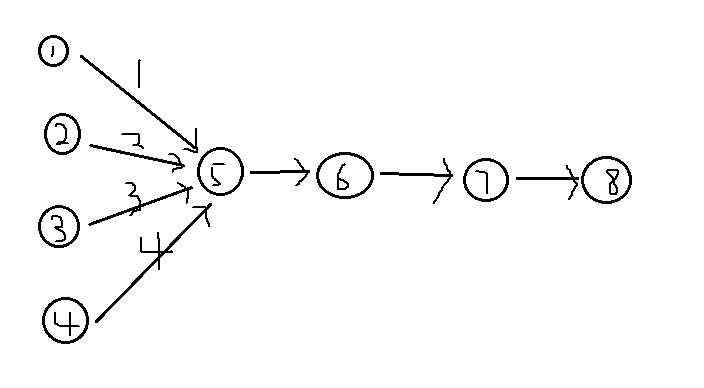
Hint

#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <vector> #include <queue> #include <cmath> #include <stack> using namespace std; #define N 100005 #define inf 999999999 int max(int x,int y){return x>y?x:y;} int min(int x,int y){return x<y?x:y;} int abs(int x,int y){return x<0?-x:x;} int dis[N], dp[N]; int n, m; bool visited[N]; int in[N]; int out[N]; struct Edge{ int u, v, next; }e[1000005]; int head[1000005]; int cnt; void setEdge(int u,int v){ e[cnt].u=u;e[cnt].v=v;e[cnt].next=head[u]; head[u]=cnt++; } /*void bfs(int u){ //bfs超时代码 queue<int>Q; while(!Q.empty()) Q.pop(); Q.push(u);visited[u]=true;dp[u]=dis[u]; int i, v; while(!Q.empty()){ u=Q.front();Q.pop();visited[u]=false; for(i=head[u];i!=-1;i=e[i].next){ if(!visited[e[i].v]&&dp[e[i].v]<dp[u]+dis[e[i].v]){ dp[e[i].v]=dp[u]+dis[e[i].v];Q.push(e[i].v);visited[e[i].v]=true; } } } }*/ void tp(){ queue<int>Q; int i, j, k; for(i=1;i<=n;i++){ if(!in[i]) Q.push(i),dp[i]=dis[i]; } int u; while(!Q.empty()){ u=Q.front();Q.pop(); for(i=head[u];i!=-1;i=e[i].next){ dp[e[i].v]=max(dp[e[i].v],dp[u]+dis[e[i].v]); in[e[i].v]--; if(!in[e[i].v]) Q.push(e[i].v); } } } main() { int i, j, k; while(scanf("%d %d",&n,&m)==2){ for(i=1;i<=n;i++) scanf("%d",&dis[i]); for(i=0;i<=n;i++) dp[i]=-inf; cnt=0; memset(head,-1,sizeof(head)); // cout<<endl; memset(in,0,sizeof(in)); memset(out,0,sizeof(out)); int x, y; while(m--){ scanf("%d %d",&x,&y); setEdge(x,y); in[y]++; out[x]++; } memset(visited,false,sizeof(visited)); tp(); int ans=-inf; for(i=1;i<=n;i++){ // printf("%d ",dp[i]); if(!out[i]&&ans<dp[i]) ans=dp[i]; } // cout<<endl; printf("%d\n",ans); } return 0; }

标签:
原文地址:http://www.cnblogs.com/qq1012662902/p/4373093.html