URAL 1507 Difficult Decision 矩阵快速幂

标签：矩阵快速幂

1507. Difficult Decision

Time limit: 1.0 second
Memory limit: 64 MB

Often, when a decision about investing in a new business must be taken, a New Russian has to estimate quickly whether a certain project will be a success or not. Leading economists have recently discovered a new algorithm for forecasting the success of a project.

First, one has to form an n × n matrix of risks. Let us denote this matrix by A. Then, in order to take into account the interdependencies of the parameters inside the matrix, the matrix

must be computed. If at least one of the elements of the matrix B is zero, then there is a considerable probability that the project will fail. Otherwise, if there are no zero elements in the matrix B, the new business will grow and flourish.

Help New Russians to make use of this algorithm. Your task is to write a program that determines the probability of the success of a project given the matrix of its risks.

Input

The first line of the input contains the dimension n of the matrix A (2 ≤ n ≤ 50). Each of the next n lines contains n numbers that forms the matrix A. Each element is a whole number in the range from 0 to 100.

Output

Output "No" if there is at least one zero element in the matrix B (so it is better not to invest in the new business). Otherwise, output "Yes".

Samples

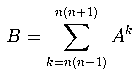
input	output
2 0 7 15 30	Yes
3 100 35 40 0 22 0 10 11 0	No

Problem Author: Evgeny Krokhalev
Problem Source: Quarter-Final of XXXI ACM ICPC - Yekaterinburg - 2006

题意：

输入A矩阵，问

，求出的B矩阵是否有0，有的话NO，没有YES。

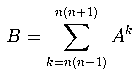
做法：

矩阵快速幂，先算出 K等于n(n-1)次的A矩阵。复杂度 是 log（n^2）*(n^3)=10^4  ，然后k循环加到 n（n+1），每次把矩阵再乘个A，然后加到B里。复杂度是 n*n^3=10^6。所以妥妥的。因为只在乎有没有0，输入只有正数，矩阵里也只有乘法和加法。所以我把非零数改成了1，然后乘法用状压位运算优化到n^2。跑得稍微快点。

#include<stdio.h>
#include<string.h>
#define Matr 60 //矩阵大小,注意能小就小   矩阵从1开始   所以Matr 要+1   最大可以100
#define ll int
struct mat//矩阵结构体，a表示内容，size大小 矩阵从1开始   但size不用加一
{
    ll a[Matr][Matr];
    mat()//构造函数
    {
        memset(a,0,sizeof(a));
    }
};
int Size;
mat add(mat m1,mat m2)
{
	for(int i=1;i<=Size;i++)
	{ 
		for(int j=1;j<=Size;j++)
		{
			if(m1.a[i][j]||m2.a[i][j])
				m1.a[i][j]=1;
		}
	}
	return m1;
}
mat multi(mat m1,mat m2)//状压，位运算
{  
    mat ans=mat(); 

	__int64 mm1[60];//一行的
	__int64 mm2[60];//一列的


	for(int i=1;i<=Size;i++)
	{
		mm1[i]=0;
		for(int j=1;j<=Size;j++)
		{
			mm1[i]<<=1;
			if(m1.a[i][j])
				mm1[i]|=1; 
		}
	}

	for(int i=1;i<=Size;i++)//列
	{
		mm2[i]=0;
		for(int j=1;j<=Size;j++)//行
		{
			mm2[i]<<=1;
			if(m2.a[j][i])
				mm2[i]|=1;
		}
	}


	for(int i=1;i<=Size;i++)
	{
		for(int j=1;j<=Size;j++)
		{
			if(mm1[i]&mm2[j])
				ans.a[i][j]=1;
		}
	}
	 
	/*
    for(int i=1;i<=Size;i++)
        for(int j=1;j<=Size;j++)
            if(m1.a[i][j])//稀疏矩阵优化 
                for(int k=1;k<=Size;k++)
                    ans.a[i][k]=(ans.a[i][k]+m1.a[i][j]*m2.a[j][k]); //i行k列第j项
					*/
    return ans;
}

mat quickmulti(mat m,ll n)//二分快速幂 
{
    mat ans=mat();
    int i;
    for(i=1;i<=Size;i++)ans.a[i][i]=1;
    while(n)
    {
        if(n&1)ans=multi(m,ans);//奇乘偶子乘 挺好记的.
        m=multi(m,m);
        n>>=1;
    }
    return ans;
}

void print(mat m)//输出矩阵信息，debug用   
{  
    int i,j;  
    printf("%d\n",Size);  
    for(i=1;i<=Size;i++)  
    {  
        for(j=1;j<=Size;j++)
			printf("%d ",m.a[i][j]);  
        printf("\n");  
    }  
}  

int judge(mat m)
{

	for(int i=1;i<=Size;i++)
	{
		for(int j=1;j<=Size;j++)
		{
			if(m.a[i][j]==0)
				return 0;  
		}
	}
	return 1;		
}
int main()
{ 
	mat gouzao=mat(),chu=mat();//构造矩阵  初始矩阵  
	mat ans=mat();

	cin>>Size;


	for(int i=1;i<=Size;i++)
	{
		for(int j=1;j<=Size;j++)
		{
			int tem;
			scanf("%d",&tem);
			if(tem)
				gouzao.a[i][j]=1;
		} 
	}
	
	chu=quickmulti(gouzao,Size*(Size-1)-1);
	
	
	for(int i=Size*(Size-1);i<=Size*(Size+1);i++)
	{ 
		chu=multi(chu,gouzao);
		ans=add(ans,chu);
	}
	
	if(judge(ans))//mei 0
		puts("Yes");

	else
		puts("No");  
	return 0;
}

URAL 1507 Difficult Decision 矩阵快速幂

标签：矩阵快速幂

原文地址：http://blog.csdn.net/u013532224/article/details/44698613