B. Mr. Kitayuta's Colorful Graph (CF #286 (Div. 2) 并查集)

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color ci, connecting vertex ai and bi.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — ui and vi.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex ui and vertex vi directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2?≤?n?≤?100,?1?≤?m?≤?100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — ai, bi (1?≤?ai?<?bi?≤?n) and ci (1?≤?ci?≤?m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i?≠?j, (ai,?bi,?ci)?≠?(aj,?bj,?cj).

The next line contains a integer — q (1?≤?q?≤?100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — ui and vi (1?≤?ui,?vi?≤?n). It is guaranteed that ui?≠?vi.

Output

For each query, print the answer in a separate line.

Sample test(s)

input
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

output
2
1
0

input
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

output
1
1
1
1
2

Note

Let‘s consider the first sample.

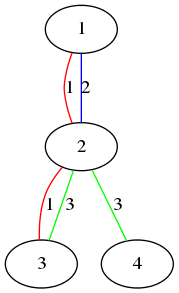$技术分享$ The figure above shows the first sample.

Vertex 1 and vertex 2 are connected by color 1 and 2.
Vertex 3 and vertex 4 are connected by color 3.
Vertex 1 and vertex 4 are not connected by any single color.

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <string> #include <map> #include <stack> #include <vector> #include <set> #include <queue> #pragma comment (linker,"/STACK:102400000,102400000") #define maxn 1005 #define MAXN 2005 #define mod 1000000009 #define INF 0x3f3f3f3f #define pi acos(-1.0) #define eps 1e-6 #define lson rt<<1,l,mid #define rson rt<<1|1,mid+1,r typedef long long ll; using namespace std; int n,m; int color[110]; int father[110][110]; void init() { for (int i=0;i<=110;i++) for (int j=0;j<=110;j++) father[i][j]=j; } int find_father(int c,int x) //递归写法 { if (x!=father[c][x]) father[c][x]=find_father(c,father[c][x]); return father[c][x]; } //int find_father(int c,int x) //非递归写法 //{ // int r=x,i,j; // while(r!=father[c][r]) // r=father[c][r]; // i=x; // while(i!=r) // { // j=father[c][i]; // father[c][i]=r; // i=j; // } // return r; //} int main() { while (~scanf("%d%d",&n,&m)) { init(); int a,b,c; memset(color,0,sizeof(color)); //记录下用了哪些颜色 for (int i=0;i<m;i++) { scanf("%d%d%d",&a,&b,&c); color[c]=1; // printf("+++\n"); int fa=find_father(c,a); int fb=find_father(c,b); if (fa!=fb) father[c][fa]=fb; } int q,x,y; scanf("%d",&q); while (q--) { scanf("%d%d",&x,&y); int ans=0; for (int i=1;i<=m;i++) { if (color[i]) { if (find_father(i,x)==find_father(i,y)) ans++; } } printf("%d\n",ans); } } return 0; }