标签:
“目标”图层是从中选择要素的图层
“源”图层是这样的图层:用户要基于该图层与目标图层的空间关系,使用该图层中的要素确定应当选择的要素。
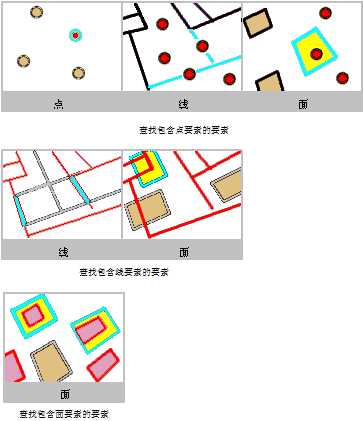
图中,选中的要素用青色高亮显示,它们与红色源要素相交、接触,或者包含在红色源要素中。
相交返回与源要素完全或部分重叠的要素。以下是一些示例:
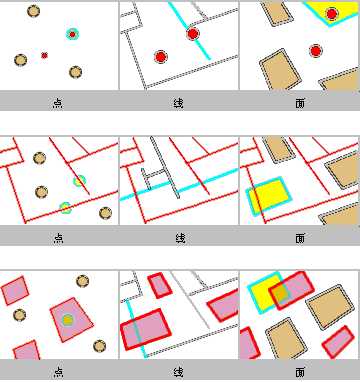
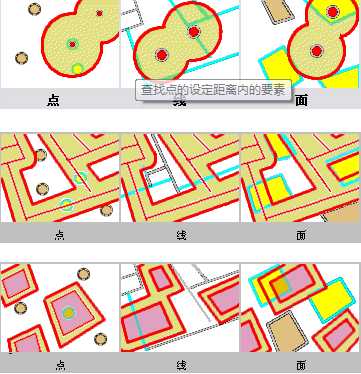
此运算符使用源要素周围的缓冲距离创建缓冲,并且返回所有与缓冲区域相交的要素。例如,选择距离河流或者铁路 100 米以内的城市。
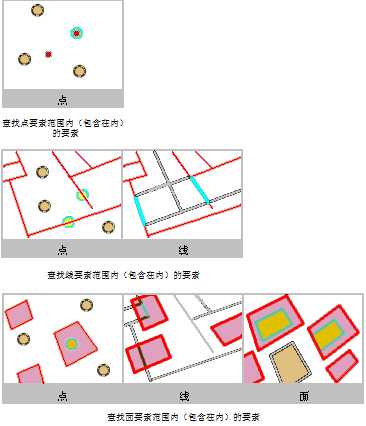
以青色高亮显示的要素被选中,因为它们落在了红色要素的选定距离中。
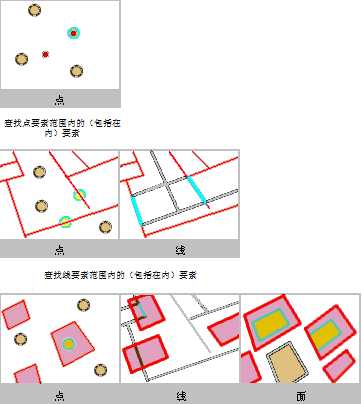
要被选中,目标要素的几何必须落在源要素的几何之内。选中的要素与源要素可有重叠的边界。
例如,使用此运算符,即使蒙大纳州与美国共享边界,也可选中蒙大纳州。
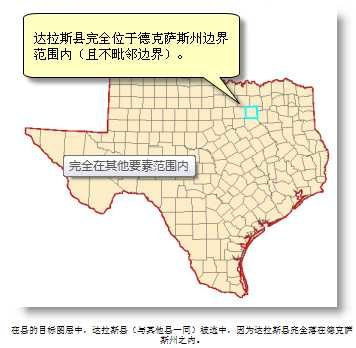
要被选中,目标要素的所有部分必须落在源要素的几何之内,并且不能接触源要素的边界。例如,在一个国家的目标图层中,达拉斯县被选中,因为它落在了德克萨斯的源面之中。这对于所有不落在德克萨斯边界上的县都适用。
此运算符与“完全包含”相反。请参阅下面以了解更多信息。源要素必须是一个面,或者您要在点或线要素周围应用缓冲以使用此运算符。
以青色高亮显示的要素被选中,因为它们完全在红色要素之内。
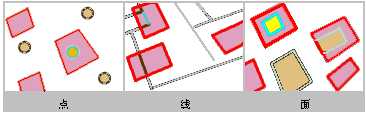
要被选中,源要素的几何(包括其边界)必须落在目标要素的几何之内。例如,一个代表美国的面包含德克萨斯州,并且即使此面与德克萨斯州共享南面的边界。此面要素仍会被选中。
这与“在其他要素范围内”的运算符相反。
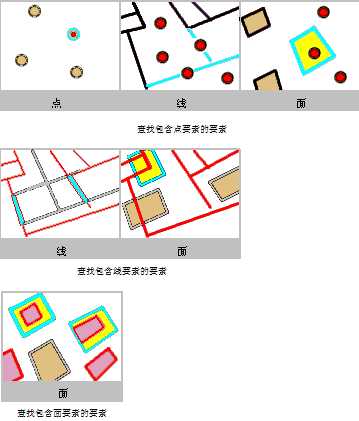
要被选择,目标要素的所有部分必须完全包含源要素的几何。此外,源要素不可接触目标要素的边界或与目标要素的边界重叠。例如,如果源要素为堪萨斯州,那么代表美国边界的要素可被选中,因为此要素完全包含堪萨斯州,并且不接触其边界。但是,如果源要素为德克萨斯州,将不会选中代表美国边界的要素,因为德克萨斯与美国边界共享边界。这与“完全在其他要素范围内”的运算符相反。
目标要素图层必须为一个面。
以青色高亮显示的要素被选中,因为它们完全包含红色要素。
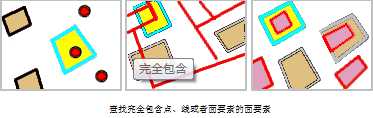
如果目标要素的几何质心落在源要素的几何之内或落在其边界上,那么使用该运算符可以选中目标要素。
以青色高亮显示的要素被选中,因为它们的质心在红色要素内。
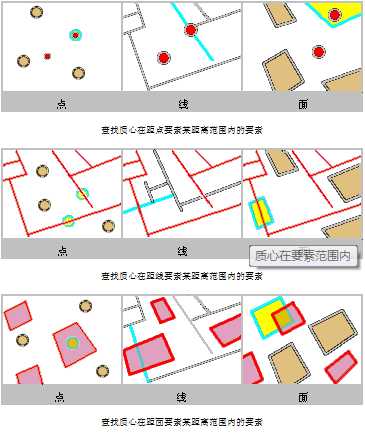
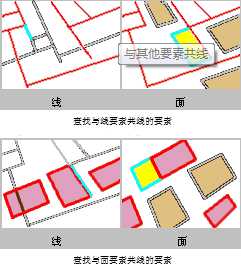
用此方法,如果源要素与目标要素的几何有至少两个共用的连续折点,那么它们将被认为共线。
源要素与目标要素必须为线要素或者面要素。
以青色高亮显示的要素被选中,因为它们与红色要素共线。
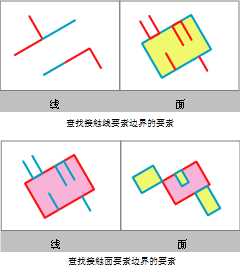
如果目标要素的几何与源要素的交集不为空,但是它们内部的交集为空,那么会选中目标要素。这是 Clementini 接触运算符的定义,所以如果目标要素接触(如 Clementini 所定义)源要素,那么目标要素会被选中。
源要素与目标要素必须为线要素或者面要素。
该运算符包含 Clementini 运算符,但对其进行了扩展。另外还支持以下情况:如果完全包含在面中的内部线或内部面的几何与该面的边界共线、共折点或者共端点,那么此内部线或者内部面会被选中。
以青色高亮显示的要素被选中,因为它们与红色要素的边界接触。
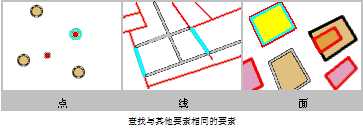
如果两个要素的几何严格相等,那么这两个要素被认为相同。要素类型必需相同,例如,您可使用此运算符来比较两个面图层,但将一个点图层与一个面图层相比会始终返回空选择集。
以青色高亮显示的要素被选中,因为它们与红色要素相同。
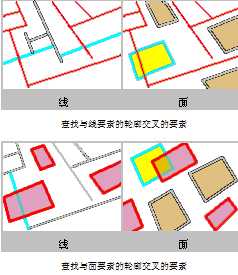
对于此运算符,它要求源要素与目标要素的边界必须至少共用一个边、折点或端点,但是不能共线。
源要素与目标要素必须为线要素或者面要素。
除非源要素完全在目标要素的边界上,且没有任何部分位于目标要素内,否则此运算符的运算结果与“包含”运算符的相同。在这种特殊情况下,使用“包含 (Clementini)”运算符不会选择目标要素,而使用“包含”运算符则会选择目标要素。Clementini 运算规定面的边界独立于面的内部和外部。
Clementini 涉及在以下文章中定义的“在其他要素范围内”与“包含”拓扑关系:Eliseo Clementini、Paolino Di Felice 和 Peter van Oosterom,适用于最终用户交互的形式化拓扑关系的小集合。第三届空间数据库研究进展国际研讨会的会议记录,第 277–295 页,1993 年 6 月 23-25 日。
以青色高亮显示的要素被选中,因为它们包含一个红色要素。
除非目标要素完全在源要素的边界上,且没有任何部分位于源要素内,否则此运算符的运算结果与“在其他要素范围内”运算符的相同。在这种情况下,使用“在其他要素范围内 (Clementini)”运算符不会选择目标要素,而使用“在其他要素范围内”运算符则会选择目标要素。Clementini 运算规定面的边界独立于面的内部和外部。
Clementini 涉及在以下文章中定义的“在其他要素范围内”与“包含”拓扑关系:Eliseo Clementini、Paolino Di Felice 和 Peter van Oosterom,适用于最终用户交互的形式化拓扑关系的小集合。第三届空间数据库研究进展国际研讨会的会议记录,第 277–295 页,1993 年 6 月 23-25 日。
标签:
原文地址:http://www.cnblogs.com/gisyang/p/4376025.html