HDU5120 Intersection 相交环面积 (2014北京现场赛)

标签：acm 计算几何 相交环

链接：click here~~

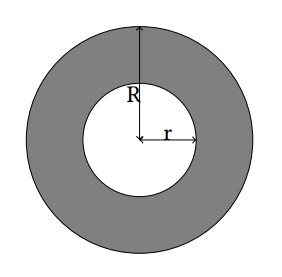
题意：求相交环面积

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

2
2 3
0 0
0 0
2 3
0 0
5 0

Case #1: 15.707963
Case #2: 2.250778

【解题思路】

  在纸上画出图来，分别标记两个圆为a圆，b圆，内圆和外圆分别为a,A,b,B不难发现，要求相交面积，如果a与b相交，一定有a与B相交，但是a与B相交，不一定a与b相交。

其实这就是容斥定理了，

  S：A与B相交面积；

  s1:a与B相交面积；

  s2:b与A相交面积；

  s3:a与b相交面积；

因此所求答案为：area=S-(s1+s2-s4);(两个内圆相交面积计算了两次)

代码：

//相交环面积
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <iostream>
#include <algorithm>
using namespace std;
const double PI=acos(-1.0);
struct point
{
    double x,y,r;
} A,B,a,b;
double dis(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double interarea(point a,point b)            
{
    double d=dis(a,b);
    if(d>=a.r+b.r)return 0;
    double r=a.r>b.r?b.r:a.r;
    if(d<=fabs(a.r-b.r))return PI*r*r;
    double angle1=acos((a.r*a.r+d*d-b.r*b.r)/2.0/a.r/d);
    double angle2=acos((b.r*b.r+d*d-a.r*a.r)/2.0/b.r/d);
    double ans=0;
    ans-=d*a.r*sin(angle1);
    ans+=angle1*a.r*a.r+angle2*b.r*b.r;
    return ans;
}
int main()
{
    int T,tot=1;
    scanf("%d",&T);
    while(T--)
    {
        double r1,r2,x1,y1,x2,y2;
        scanf("%lf%lf%lf%lf%lf%lf",&r1,&r2,&x1,&y1,&x2,&y2);
        A.r=r2,a.r=r1,A.x=a.x=x1,A.y=a.y=y1;
        B.r=r2,b.r=r1,B.x=b.x=x2,B.y=b.y=y2;
        double S=interarea(A,B);         //S：A与B相交面积；
        double s1=interarea(a,B);        //s1:a与B相交面积；
        double s2=interarea(A,b);        //s2:b与A相交面积；
        double s3=interarea(a,b);        //s3:a与b相交面积；
        double area=S-(s1+s2-s3);
        printf("Case #%d: ",tot++);
        printf("%.6lf\n",area);
    }
    return 0;
}

HDU5120 Intersection 相交环面积 (2014北京现场赛)

标签：acm 计算几何 相交环

原文地址：http://blog.csdn.net/u013050857/article/details/44807435