数学之路-SAS分析(1)

标签：大数据   sas   

卡方分布（chi-square distribution, χ2-distribution）是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。卡方分布是一种特殊的伽玛分布，是统计推断中应用最为广泛的概率分布之一，例如假设检验和置信区间的计算。

若k个随机变量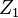、……、是相互独立，符合标准正态分布的随机变量（数学期望为0、方差为1），则随机变量Z的平方和

被称为服从自由度为 k 的卡方分布，记作

概率密度函数

其中，

是伽玛函数。

期望和方差

分布的均值为自由度 n，记为 E(

) = n。

分布的方差为2倍的自由度(2n)，记为 D(

) = 2n。

性质

1)

分布在第一象限内，卡方值都是正值，呈正偏态（右偏态），随着参数 n 的增大，

分布趋近于正态分布；卡方分布密度曲线下的面积都是1.

2)

分布的均值与方差可以看出，随着自由度n的增大，χ2分布向正无穷方向延伸（因为均值n越来越大），分布曲线也越来越低阔（因为方差2n越来越大）。

4) 若

互相独立，则：

服从

分布，自由度为

；

服从

分布，自由度为

。

累积分布函数

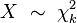
卡方分布的累积分布函数为：

，

其中γ(k,z)为不完全Gamma函数

在大多数涉及卡方分布的书中都会提供它的累积分布函数的对照表。此外许多表格计算软件如OpenOffice.org Calc和Microsoft Excel中都包括卡方分布函数。

自由度为k的卡方变量的平均值是k，方差是2k。 卡方分布是伽玛分布的一个特例，它的熵为：

其中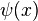是双伽玛函数。

伽玛函数（Gamma Function）作为阶乘的延拓，是定义在复数范围内的亚纯函数，通常写成

。

其中

，此定义可以用解析开拓原理拓展到整个复数域上，非正整数除外。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数均数为0, 尺度参数：标准差为1的正态分布（见右图中绿色曲线）。

正态分布中一些值得注意的量：

密度函数关于平均值对称

平均值与它的众数（statistical mode）以及中位数（median）同一数值。

函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。

95.449974%的面积在平均数左右两个标准差的范围内。

99.730020%的面积在平均数左右三个标准差的范围内。

99.993666%的面积在平均数左右四个标准差的范围内。

函数曲线的反曲点（inflection point）为离平均数一个标准差距离的位置。

非中心卡方分布^[1][2]是有正态分布衍生得到的一个概率分布. 设为一组独立的随机变量, 并且(服从正态分布), 定义随机变量, 称随机变量服从自由度为, 非中心参数为的的非中心卡方分布, 记为; 其中. 当时, 随机变量服从自由度为的卡方分布.

SAS设定自由度和非中心参数计算p分位点的方式如下：

272  data _null_;
273  q=cinv(0.95,10,25.2);*0.95分位数,自由度为10，非中心参数为25.2;
274  put q=;
275  run;


q=54.759186647
NOTE: “DATA 语句”所用时间（总处理时间）:
      实际时间          0.00 秒
      CPU 时间          0.00 秒

数学之路-SAS分析(1)

标签：大数据   sas   

原文地址：http://blog.csdn.net/myhaspl/article/details/44807445