泰勒级数

标签：

一：函数的泰勒级数：设函数f(x),在点x0具有任意阶导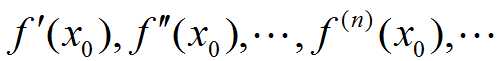数  称级数

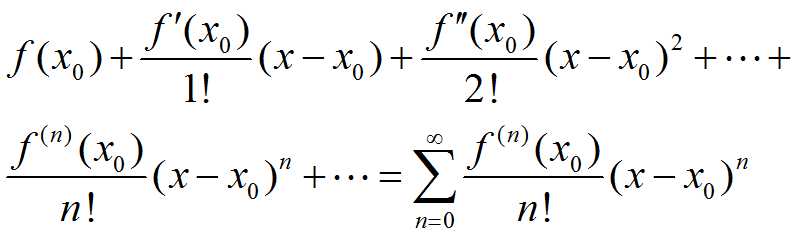
为函数f(x) 的泰勒级数，显然只要函数存在任意阶导数，其泰勒级数必存在，例如  

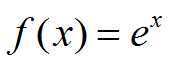在点x=0处的泰勒级数为：

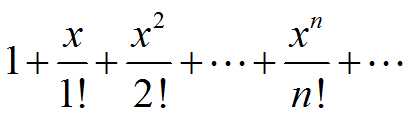
函数  f(x) 在x=0处的泰勒级数常称f(x)的马克劳林级数

一般初等函数的泰勒级数都是存在的              

函数能展开成幂级数的必要条件：如果函数f(x)在x0可以展开成幂级数，则只能展开成它自身的泰勒级数

证明:

注：必要条件说明两个问题：

1.函数在某点要想展开成幂级数，其在该点的泰勒级数必须存在，即必须有任意阶导数，反之如果级数不存在任意阶导数，必不可展成幂级数,例如：

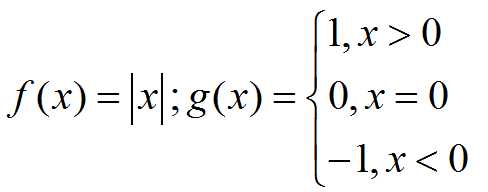
在x=0处都不能展成幂级数；

2.如果函数能展成幂级数则必唯一，即是自身的泰勒级数（这一点以后在讲间接展开时要用到）

需要说明的是当函数在某点不存在任意阶导数时不能展成幂级数，即使函数在该点存在任意阶导数，因而存在泰勒级数，也不一定就可展成幂级数，我们有：

（充要条件）设函数  f(x)  在点  x₀  存在任意阶导数，则其可在该点处展成泰勒级数的充要条件为：其n项后的余项 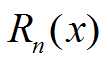    趋向于0，即

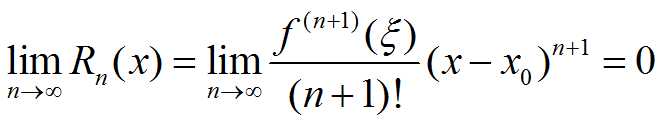
二：常用函数的泰勒级数

1：几何级数

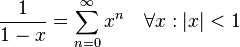
2：二项式定理

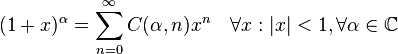
二项式展开中的C(α,n)是二项式系数。

3：指数函数

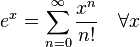
4：自然对数

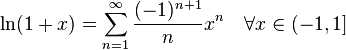
5：三角函数

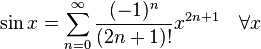
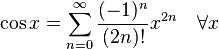
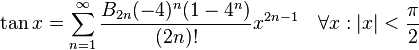
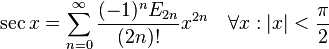
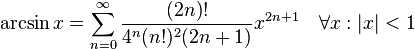
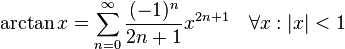
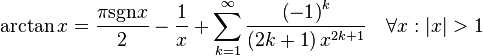
tan(x)展开式中的B_k是伯努利数。sec(x)展开式中的E_k是欧拉数。

6：双曲函数

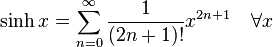
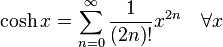
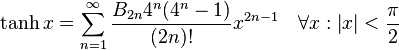
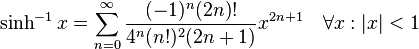
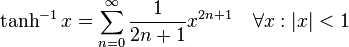
7：郎伯W函数

泰勒级数

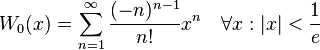
标签：

原文地址：http://www.cnblogs.com/javaleon/p/4388697.html