标签：
这场比赛特点在于两个简单题太坑，严重影响了心情。。导致最后只做出两题....当然也反映出心理素质的重要性
1002：
题意：一个矩阵b[n][n]通过数组 a[n]由以下规则构成，现在已知b[n][n]问是否有对应的数组a[n]
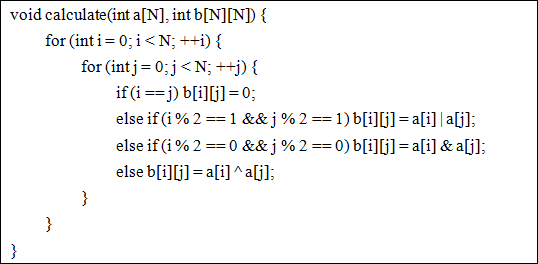
解法：
首先都是位运算所以不同位是不会互相影响的，即可按位考虑。
又发现，只要知道a[0]就可以算出通过b[0][]算出所有的a[]，这样可以假设a[0]为0或1，由b[0][]得到一个完整的数组a[]，再check这个数组a是否能正确的得到其他的b[][]即可
时间复杂度约为32*2*n^2 对于n=1000是可以接受的
当然队友是用2-SAT做的 吊吊吊吊吊orz 我就没写了，这里贴上队友的代码
代码：
#include<cstdio> #include<vector> #include<cstring> #include <iostream> #include <stdio.h> using namespace std; const int maxn = 510; struct TwoSAT { int n; vector<int> G[maxn * 2]; bool mark[maxn * 2]; int S[maxn * 2], c; bool dfs(int x) { if(mark[x ^ 1]) return false; if(mark[x]) return true; mark[x] = true; S[c++] = x; for(int i = 0; i < G[x].size(); i++) if(!dfs(G[x][i])) return false; return true; } void init(int n) // 一定要注意初始化的点数，别弄错 { this->n = n; for(int i = 0; i < n * 2; i++) G[i].clear(); memset(mark, 0, sizeof(mark)); } // x = xval or y = yval void add_clause(int x, int xval, int y, int yval) // 编号从0~n-1 { x = x * 2 + xval; y = y * 2 + yval; G[x ^ 1].push_back(y); G[y ^ 1].push_back(x); } // 当x==xval 时可推导出 y==yval void add_edge(int x, int xval, int y, int yval) { x = x * 2 + xval; y = y * 2 + yval; G[x].push_back(y); } bool solve() { for(int i = 0; i < n * 2; i += 2) if(!mark[i] && !mark[i + 1]) { c = 0; if(!dfs(i)) { while(c > 0) mark[S[--c]] = false; if(!dfs(i + 1)) return false; } } return true; } }; TwoSAT solver; int n; int a[maxn][maxn]; bool check(int l) { solver.init(n); for(int i = 0; i < n; i++) for(int j = 0; j < n; j++) { int bit = (a[i][j] & (1 << l))>>l; if(i == j) { if(a[i][j] != 0) { return false; } } else if(a[i][j] != a[j][i]) { return false; } else if(i % 2 == 0 && j % 2 == 0) // & { solver.add_edge(i, 1, j, bit); solver.add_edge(j, 1, i, bit); if(bit) { solver.add_edge(i, 0, i, 1); solver.add_edge(j, 0, j, 1); } } else if(i % 2 == 1 && j % 2 == 1) // | { solver.add_edge(i, 0, j, bit); solver.add_edge(j, 0, i, bit); if(!bit) { solver.add_edge(i, 1, i, 0); solver.add_edge(j, 1, j, 0); } } else // ^ { solver.add_edge(i, 1, j, bit ^ 1); solver.add_edge(j, 1, i, bit ^ 1); solver.add_edge(i, 0, j, bit); solver.add_edge(j, 0, i, bit); } } return solver.solve(); } int main() { while(~scanf("%d", &n)) { for(int i = 0; i < n; i++) for(int j = 0; j < n; j++) { scanf("%d", &a[i][j]); } bool flag = true; // 枚举每一位,l为座椅的 位数 for(int l = 0; l <= 31; l++) { if(!check(l)) { flag = false; break; } } puts(flag?"YES":"NO"); } return 0; }
1003：
题意：
这个简单题题意挺恶心的。。先开始一直没读懂。。
小明要在五座山上采五堆蘑菇，每堆的个数是0~2012，采完后必须送出三堆和为1024倍数的蘑菇（否则全送出），回家之前如果总数大于1024还要一直被抢1024。
现在已经采了n堆（n<=5），剩下的可以任意采（0~2012）问最终最多能拿回家多少蘑菇.
解法：
分情况特判.....以下省略好多字
代码：
#include <set> #include <map> #include <cmath> #include <ctime> #include <queue> #include <stack> #include <cstdio> #include <string> #include <vector> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef unsigned long long ull; typedef long long ll; const int inf = 0x3f3f3f3f; const double eps = 1e-8; int a[6]; const int mod = 20121024; int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif int n; while (~scanf ("%d", &n)) { memset(a, 0, sizeof(a)); int sum = 0; for (int i = 0; i < n; i++) { scanf ("%d", a+i); sum += a[i]; } int ans = 0, res = 0; if (n<=3) { printf("%d\n", 1024); continue; } if (n == 4) { int ans = 0; bool flag = 0; for (int i = 0; i < 4; i++) { for (int j = i+1; j < 4; j++) { int tmp = a[i]+a[j]; if (tmp) ans = max(ans, (tmp%1024) ? (tmp%1024) : 1024); for (int k = j +1; k < 4; k++) { if ((a[i] + a[j] + a[k]) % 1024 == 0) flag = 1; } } } if (flag) printf("%d\n" , 1024); else printf("%d\n" ,ans); continue; } if (n == 5) { bool f = 0; int ans = 0; for (int i = 0; i < 5; i++) { for (int j = i+1; j < 5; j++) { for (int k = j+1; k < 5; k++) { int tmp = a[i] +a[j] +a[k]; if (tmp % 1024 == 0) { if (sum-tmp) ans = max(ans, ((sum-tmp)%1024) ? (sum-tmp)%1024 : 1024); } } } } printf("%d\n",(ans > 1024) ? (ans %1024) : ans); } } return 0; }
1004：
题意：
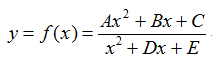求y的取值范围
思路：
高中数学题，移项得到一个二次函数，然后各种分类讨论，太麻烦了没敢写。。。
1005：
队友做的 先挖坑
1008：
题意：
知道n个数的和sum，以及n个数的LCM，求合法的组成方案（排列）
解法：
发现lcm的转移只可能通过lcm的约数，（一开始和分解质因数搞呢，后来经过学长提醒发现直接找出约数即可 orz），约数数量不是很多。。这样就可以dp了
把约数哈希一下 dp[i][j][k]代表考虑到第i个数，当前lcm为总LCM的第j个约数，当前sum为k的方案数，转移很容易
代码：
#include <iostream> #include <stdio.h> #include<string.h> #include<algorithm> #include<string> #include<ctype.h> using namespace std; #define MAXN 10000 const int mod=1e9+7; bool is(int p) { for(int i=2; i*i<=p; i++) { if(p%i==0) return 0; } return 1; } int gcd(int a,int b) { return b==0?a:gcd(b,a%b); } int lcm(int a,int b) { return a/gcd(a,b)*b; } int prime[1010]; int s[50]; int dp[110][1100][50]; int a[1010]; int ha[1010]; int l[50][50]; int sum,L,n,m; int main() { // freopen("in.txt","r",stdin); m=0; for(int i=2; i<=1000; i++) { if(is(i)) { prime[m++]=i; } } while(scanf("%d%d%d",&sum,&L,&n)!=EOF) { memset(ha,-1,sizeof(ha)); int lim=0; for(int i=1;i<=L;i++) { if(L%i==0) { ha[L/i]=lim; s[lim++]=L/i; } } for(int i=0;i<lim;i++) { for(int j=0;j<lim;j++) { l[i][j]=lcm(s[i],s[j]); } } memset(dp,0,sizeof(dp)); dp[0][0][lim-1]=1; for(int i=1;i<=n;i++) { for(int j=0;j<=sum;j++) { for(int k=0;k<lim;k++) { if(!dp[i-1][j][k]) continue; for(int t=0;t<lim;t++) { if(j+s[t]<=sum) { if(ha[l[k][t]]==-1) continue; dp[i][j+s[t]][ha[l[k][t]]]+=dp[i-1][j][k]; dp[i][j+s[t]][ha[l[k][t]]]%=mod; } } } } } cout<<dp[n][sum][0]<<endl; } return 0; }
1010：
题意：
一个大矩形被一些线段分成了小矩形，现在给定两个点的坐标，求出删除一些线段使这两点在同一矩形后剩余矩形数量的最大值。
思路：
其实就是要找所求两点共同所在的最小的矩形（除此之外的线段都不删除，得到的剩余矩形数肯定最多）。
而按照题意的分割矩形法其实就是形成了一颗树，这样就发现两个点所在的最小矩形其实是这两个点当前所在矩形的lca
理论ac了。。代码还没写
1011:
题意：
给定一个等比数列 1(或者0)+k+k^2+....k^r的和 S，要求求出r 和k，多解首先满足r*k最小，然后满足 r最小
解法：
由于k>=2所以可以计算发现r最大为40，则可以枚举r，二分求得k ，如果r和二分出的k刚好等于 k或者k-1 则符合题意，可以统计答案
坑点是二分过程中容易溢出
代码：
#include <iostream> #include <stdio.h> using namespace std; typedef long long ll; ll n; ll equ(ll ak , int r) { ll ans = 1; ll k = ak; for(int i = 1; i <= r; i++) { ans += k; if(ans > n + 1) break; if(ans<=0) return 10000000000000LL; k *= ak; } return ans; } int main() { while(~scanf("%I64d", &n)) { ll ansk = 10000000000000LL; int ansr = 100; // 枚举r for(int r = 1; r <= 40; r++) { // 二分k ll l = 1, R = 1000000000001LL; while(l < R) { ll m = (l + R + 1) / 2; if(equ(m, r) <= n) { l = m; } else { R = m - 1; } } ll k = l; if(equ(k, r) == n) { // 保存答案 if((ansk * ansr > k * r) || ((ansk * ansr == k * r) && ansr > r)) { ansk = k; ansr = r; } } // 二分k l = 1, R = 1000000000001LL; while(l < R) { ll m = (l + R + 1) / 2; if(equ(m, r) <= n + 1) { l = m; } else { R = m - 1; } } k = l; if(equ(l, r) == n + 1) { // 保存答案 if((ansk * ansr > k * r) || ((ansk * ansr == k * r) && ansr > r)) { ansk = k; ansr = r; } } } printf("%d %I64d\n", ansr, ansk); } return 0; }
标签：
原文地址：http://www.cnblogs.com/oneshot/p/4389511.html
