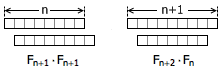标签:acm poj
Fibonacci数列的定义如下:
f(n) = f(n - 1) + f(n - 2) (n >= 3)
f(1) = 1, f(2) = 2
f(0)可定义为1。
用归纳法可以证明性质:
f(n + m) = f(m - 1)f(n + 1) + f(m - 2)f(n) (m>= 2)
利用这条性质,我们可以将比较大的n的Fibonacci数转化成比较小的Fibonacci数,从而使计算起来更为方便。
这里有一个问题:
Fibonacii数列 Fn (mod k) 的循环节长度是多少?有没有关于k的通项公式或者计算方法?
实例
PKU JudgeOnline, 3070, Fibonacci.
问题描述
给定n,要求第n个Fibonacci数mod 10000的结果。
输入
0
9
999999999
1000000000
-1
输出
0
34
626
6875
分析
可以通过Fibonacci的性质和模运算的性质对之进行递归求解。通过鸽巢原理可以知道输出必定是一个循环。如果知道循环节,该问题就更简单了。循环节也很好找。
此题目输入数据较大,时间开销不允许这么大,同时,另一种思路就是用数组记录计算出的结果,这种做法貌似可以,但是主要题目中有内存限制,对于输入1000000000这样大的数据,显然要建立这样的数组是不允许的,基于此,采用部分标记数组(因为越底层计算次数就越多,所以只要范围选取合适,完全可以满足本题目的需要),同时采用fibonacci卷积的公式计算,效果应该会更好一些。
fibonacci性质很多:
1.f(0)+f(1)+f(2)+…+f(n)=f(n+2)-1
2.f(1)+f(3)+f(5)+…+f(2n-1)=f(2n)-1
3.f(0)+f(2)+f(4)+…+f(2n)=f(2n+1)-1
4.[f(0)]^2+[f(1)]^2+…+[f(n)]^2=f(n)·f(n+1)
5.f(0)-f(1)+f(2)-…+(-1)^n·f(n)=(-1)^n·[f(n+1)-f(n)]+1
6.f(m+n)=f(m-1)·f(n-1)+f(m)·f(n)
7.[f(n)]^2=(-1)^(n-1)+f(n-1)·f(n+1)
8.f(2n-1)=[f(n)]^2-[f(n-2)]^2
9.3f(n)=f(n+2)+f(n-2)
10.f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m) [ n〉m≥-1,且n≥1]
11 f(k+n)=f(k)*f(n+1)+f(k-1)*f(n)
此题目选用的是公式11的变形(fibonacci卷积公式)
分别令k=n和k=n+1即可获得奇数相的关系和偶数项的关系
F[N]=F[N/2]*F[N/2+1]
+ F[N/2-1]*F[N/2];当N为偶数的时候
F[N]=F[N/2+1]*F[N/2+1] + F[N/2]*F[N/2];当N为奇数的时候
参考源码:
/*poj3070*/
#include <iostream>
#define maxSize 5000000
using namespace std;
int F[maxSize];
int fibonacci(int n,int mod)
{
if(n==0)
return 0;
if(n==1)
return 1;
if(n==2)
return 1;
if(n<maxSize&&F[n])
return F[n];
int temp;
/*
*使用fibonacci的卷积公式:
*F[N]=F[N/2]*F[N/2+1] + F[N/2-1]*F[N/2];当N为偶数的时候
*F[N]=F[N/2+1]*F[N/2+1] + F[N/2]*F[N/2];当N为奇数的时候
*/
if(n%2==0)/*odd*/
temp=(fibonacci(n/2,mod)*fibonacci(n/2+1,mod)+fibonacci(n/2-1,mod)*fibonacci(n/2,mod))%mod;
else
temp=(fibonacci(n/2+1,mod)*fibonacci(n/2+1,mod)+fibonacci(n/2,mod)*fibonacci(n/2,mod))%mod;
if(n<maxSize)
F[n]=temp;
return temp;
}
int main(int argc , char** argv)
{
int n;
F[1]=1;
F[2]=1;
F[3]=2;
while(cin>>n&&n!=-1)
{
cout<<fibonacci(n,10000)<<endl;
}
return 1;
}
附
Fibonacci数列性质的组合证明
数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质,其中一个性质是,每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积一定正好相差 1 。具体地说,如果把第 n 个 Fibonacci 数记做 Fn ,那么有:
Fn+1 · Fn+1 –
Fn · Fn+2 = (-1)n
今天看到了这个定理的一个组合数学证明,觉得非常有意思,在这里和大家分享。
Fibonacci 数有很多组合数学上的意义。比如说,用 1 × 1 和 1 × 2 的积木覆盖一个 1 × n 的棋盘,总的方案数恰好是 Fn+1 。下图显示的就是 n 较小时的一些实例:
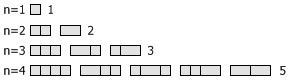
这个规律背后的原因其实很简单:给出一个长度为 n 的棋盘后,它的覆盖方案可以分成两类,最后边放的是一个 1 × 1 的积木,或者最后边放的是一个 1 × 2 的积木。前一类情况下的方案数也就完全取决于前 n – 1 个格子的覆盖方案数,后一类情况下的方案数则等于前 n – 2 个格子的覆盖方案数。因此,如果用 f(n) 来表示 1 × n 棋盘的覆盖方案数,那么正好就有 f(n) = f(n – 1) + f(n – 2) 。另外,由于 f(1)
= 1 , f(2) = 2 ,因而接下来的数 f(3), f(4), f(5), … 也就恰好构成了 Fibonacci 数列。
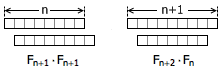
既然这样,那么用积木覆盖两个独立的 1 × n 棋盘,总方案数就是 Fn+1 · Fn+1 。我们有意把这两个独立的棋盘像左图那样摆放。类似地,用积木覆盖一个
1 × (n+1) 棋盘加上另一个 1 × (n-1) 棋盘的总方案数则为 Fn · Fn+2 ,我们把这两个棋盘放成右图所示的样子。左图的覆盖方案和右图的覆盖方案之间有一种非常巧妙的一一对应关系。

对于左图中的任意一种覆盖方案,我们找出上下两块棋盘中所有位置重合的“公共分割线”,选出最右边的那条公共分割线,然后交换此分割线右侧的部分。这样,左图棋盘的每个覆盖方案就能变成右图棋盘的一个覆盖方案。根据同样的方法,右图棋盘的每个覆盖方案也能变回左图棋盘的覆盖方案,这就说明了 Fn+1 ·
Fn+1 和 Fn · Fn+2 是相当的。
等等,那为什么当 n 为偶数时, Fn+1 · Fn+1 比
Fn · Fn+2 要大 1 ,而 n
为奇数时, Fn+1 · Fn+1 会比
Fn · Fn+2 小 1 呢?神就神在这里。这是因为,刚才所说的一一对应关系并不是真的完全一一对应的。当
n 为偶数时,左图棋盘有一例极其特殊的覆盖方案无法对应到右图的棋盘——因为这种方案中根本没有公共分割线。当 n 为奇数时,左图的棋盘就不再有如此特殊的覆盖方案了,但右图棋盘中却又多出了一例没有公共分割线的情况。这就证明了 Fn+1 · Fn+1 –
Fn· Fn+2 = (-1)n 。

fibonacci卷积公式的使用
标签:acm poj
原文地址:http://blog.csdn.net/u011889952/article/details/44852745