标签:
让我们用一道题来说明这个问题吧
题目连接:http://poj.org/problem?id=1182
我们先不妨假设a与b是同类的时候偏移量为0
a吃b的时候偏移量1
a被b吃的时候偏移量为2 a的父亲节点为aa b的父亲节点为bb
有了这个假设,那下面就能很方便解决这个问题了
我们先查找给出节点的父亲节点然后看看父亲节点的是不是相同的 如果是不相同的那么我们就更新b的父亲节点的偏移量
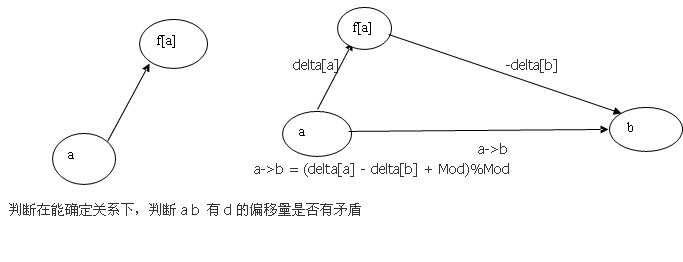
先看一张图片
由图片可知 p[fx].relation = (3 + p[y].relation - p[x].relation + d - 1) % 3; 对3取余是为了让他在1 和2之间-p[x].relation表示从x到x的父节点的偏移量d-1是x到y的偏移量p.relation表示偏移量
如果父节点相同的话 那我们就检验两个节点的关系是否与给出的d相同
如果相同就continue 如果不同就让假话次数+1
总结:
向量偏移其实就是并查集的变形,但是他有一个局限性 局限于种类少的题目 这样才能用向量偏移
其实向量偏移就是在初始化的时候给数组加一个属性 就是偏移量,然后去更新这些偏移量来判断是否正确
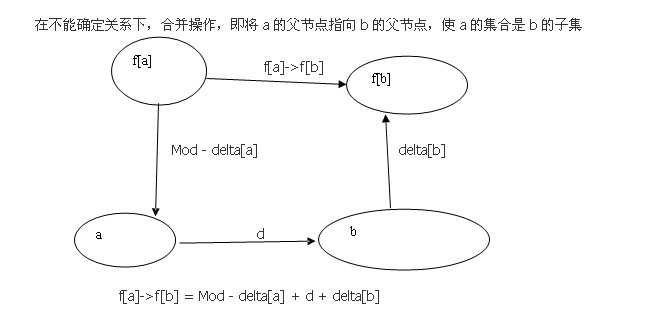
这两张图片看懂了就能明白向量偏移了
下面看代码:
#include<stdio.h> #include<math.h> #include<string.h> #include<algorithm> #include<iostream> using namespace std; struct node { int bin; int relation; }p[50005]; int findx(int x) { int t; if(p[x].bin == x)return x; else { t = p[x].bin; p[x].bin = findx(t); p[x].relation = (p[x].relation + p[t].relation) % 3; //更新x对根的偏移量 } return p[x].bin; } void join(int x,int y,int fx,int fy,int d) { p[fx].bin = fy; p[fx].relation = (3 + p[y].relation - p[x].relation + d - 1) % 3; //更新x根的偏移量 // 画图可知 x的根的偏移量为这个公式 } int main() { int n,k,d,x,y,fx,fy,i,sum; scanf("%d%d",&n,&k); for(i = 1;i <= n;i++) { p[i].bin = i; p[i].relation = 0; } sum = 0; while(k--) { scanf("%d%d%d",&d,&x,&y); fx = findx(x); fy = findx(y); if(x > n|| y > n||(d == 2&& x == y))sum++; else { if(fx != fy) join(x,y,fx,fy,d); else //如果跟节点相同就判断两个点与跟的关系 { if(d == 1&&p[x].relation != p[y].relation) sum++; else if(d == 2&&(p[x].relation - p[y].relation + 3) % 3 != 1) sum++; } } } printf("%d\n",sum); }
标签:
原文地址:http://www.cnblogs.com/zhanyage110/p/4394716.html