标签：
并查集是一种树型的数据结构，其保持着用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。支持三种操作：
1.并查集的数组表示
//x表示元素,s[x]表示x所属集合 int s[N]; Make-Set(x){ s[x] = x; } Find-Set(x){ return s[x]; } //将y在所属集合并入x所属集合 Union(x,y){ int temp = s[y]; //遍历所有元素,将和y在同一集合的元素并入x所属集合 for(int i=0;i<N;i++){ if(s[i]==temp){ s[j] = s[x]; } } }
在Kruskal算法中我用的就是这种方法.当然也可以用链表表示,就不详细介绍了.思路如下:
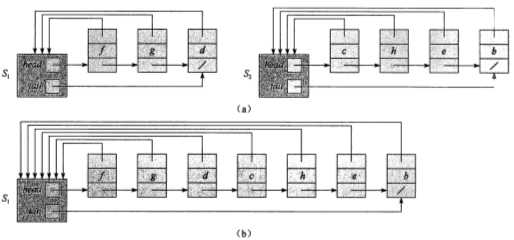
//所需数据结构 class Node; class Head{ Node* head; Node* tail; }; class Node{ Head* head; char vertex; Node* next; };
2.并查集深林
用有根树表示集合,树中的每一个结点代表一个成员,每棵树代表一个集合.在一个并查集深林中,每个成员仅指向其父结点,每棵树的树根是集合的代表,它的父结点指向自己.
Make-Set(x) x.p = x x.rank = 0 //按秩合并 Union(x,y) Link(Find-Set(x),Find-Set(y)) Link(x,y) if x.rank > y.rank y.p = x else x.p = y if x.rank==y.rank y.rank = y.rank +1 //路径压缩 Find-Set(x) if x ≠ x.p x.p = Find-Set(x.p) return x.p
它使用O(n)的空间（
为元素数量），单次操作的均摊时间为O(α(n)),α(n)≤4,总的运行时间为O(mα(n)),m为所有操作的次数.
实现:
#include<iostream> #include<vector> class Node{ int x; int rank = 0; Node* p; Node(int m):x(m){} }; vector<Node> S; void Make-Set(x){ Node node = Node(x); node.p = &node; S.push_back(node); } Node* Find-Set(x){ if(S[x] != S[x].p){ S[x].p = Find-Set(S[x].p); } return S[x].p; } void Union(x,y){ Link(Find-Set(x),Find-Set(y)); } void Link(x,y){ if(x->rank > y->rank){ y->p = x; } else{ x->p = y; if(x->rank == y->rank){ y->rank = y->rank +1; } } }
标签：
原文地址：http://www.cnblogs.com/bukekangli/p/4396385.html
