标签:
NormalMap的实现标志着对渲染流水线的各个环节以及矩阵变化有了正确和深入的认识。这里记录一下学习过程,以及关于NormalMap的诸多细节。
刚开始想要实现NormalMap程序的时候,查阅的是《Real Time Rendering》和橙皮书。这本书里从纹理映射开始讲,提到Normal Map是Bump Map的一种,原理都是利用纹理中记录的值来干扰光照方程中的法线参数,以达到改变光照结果,模拟表面细微纹理的作用。只不过,在Normal Map 中保存的就是一个法向量,直接使用即可。但是,对于这类技术,只使用于对表面凹凸效果不明显的物体,如皱纹,橘子皮上的褶皱。但是要模拟一个具有巨大山脉的自转星球时,当山脉位置旋转到星球的边缘时,看到的依然时一个光滑的球的边缘,看不到突出的部分。
考虑光照方程,里面需要有观察方向,灯光方向,以及法线的相关运算。这就要求三个向量必须在同一个坐标系中,否则相关运算不成立。这时考虑各种坐标系,看看那一种比较符合。
如果Normal Map中的记录的法线是相对与世界坐标系而言的。这样虽然可以很方便的进行计算(因为视线方向和光线方向不用转化),但是对于使用Normal Map的物体而言,其任何刚体变化都要作用于Normal Map中所记录的向量。并且,对于使用同一张Normal Map 的不同物体,两个物体的位置,朝向不同,那么对于同一张Normal Map要做两次运算,这是不划算的。
如果Normal Map在物体空间中,这时够对物体进行各种刚体变化,但是,依然不能对物体进行非刚体的变化。并且,依然存在使用同一张Normal Map 的物体的不同部分,要进行多余的处理。
并且注意到,因为读取Normal Map中的向量数据是在frangment shader中,那么对于Normal Map中的各种数据的操作都是像素级别的(因为是光栅化),计算量十分大。因此对于Normal Map中的数据进行坐标系的转化是很不明智的。
因此,我们引入了一个新的坐标系统,这个坐标系统是是相对于物体的表面面片的,这样,使用不同面片时,使用不同的坐标系进行转化既可。因为这个坐标系中包含了一个成为切线的向量,所以通常叫做切线空间(Tangent Space)。这里涉及到的变化和将物体从世界坐标系变化到物体坐标系中时的原理时一样的,所以他们的矩阵也是极为相似的。
一旦涉及到坐标系,那么必然有两个要确定的地方,一,坐标系相对与另一个坐标系的原点是哪里?二,坐标系的三个基向量相对与另一个坐标系的值是什么?如果看不懂这两个问题,请看这篇帖子。
上面提到,切线空间是相对于物体表面面片的坐标系,而定义面片的点又是在物体坐标系下定义的,那么上面提到的另一个坐标系就是相对与物体坐标系了。
对于第一个问题,考察我们引入切线空间(坐标系)的初衷,就是为了应对当物体做任何变化时,都可以正确的解读Normal Map中的向量。因为对物体做的变化是对物体的点进行各种操作的。所以,如果这个坐标系是和物体顶点坐标绑定的,那么不论对物体做何种变化,都不会影响Normal Map的解读。因此,切线空间的原点是相对与物体的顶点而言的。也就橙皮书上说的,任何传入的(x ,y,z)都将转化为(0 , 0, 0)。也就是说,坐标系是每个顶点一个的,并且以顶点为原点。进一步考虑,如果面片和Normal Map纹理都是连续体,也就是说,我们可以知道面片内部任何一个点的坐标,以及它对应的Normal Map纹理坐标,这样对于这个点我们就可以建立一个切线空间坐标系,得到的Normal Map纹理的值就是这个坐标系下的一个坐标。从这个意义上来看,我可以认为,每个纹素一个坐标系,坐标系的原点就是纹素的中心。
也就是说,如果你将一张1024*1024的Normal Map贴到一个正方形上,那么在这个正方形上就有1024*1024个切线空间。但是,在实际的计算过程中,我们会使用插值技术来避免求解这么多的切线空间。具体后面会讲。
那么第二个问题,这个比较简单。我们知道,面片由点组成的,一个三角形面片,有三个顶点。点是有法向量的N,然后对于这个点,我们还可以定义一个切向量T,这样,利用这两个向量之间的叉乘,可以得到另一向量B,通常B称为副法向量。因为通常法线N是和面片垂直的,所以切线方向一般在面片上。这样,三个向量组成了一个坐标系。这个过程是不是很熟悉?对的,就是求解从世界坐标系转化到摄像机坐标系的矩阵的过程。那么,从物体坐标系转化到切线空间坐标系的矩阵如下:

那么,是不是任何一个切向量都可以呢?理论上是可以的,但是要求你给每个纹素一个切线空间。所以,我们从计算上考虑,选择切向量的要求是尽量使得一个面片的顶点切线方向一致,比如一个三角形,三个顶点的切线方向尽量指向一个方向,并且在面片上。下图可以告诉我们是这么从计算上考量的,注意,该图中面片的法线是垂直于屏幕的:
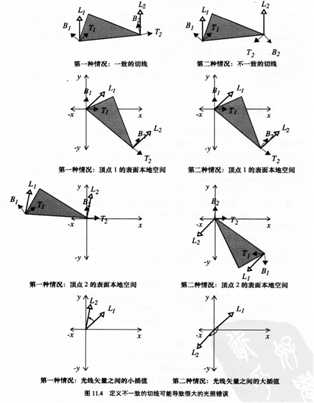
左面一列是在切向量比较一致的情况下的结果,右面是相差较大的结果。这里对上图解释一下,我们计算坐标系的原因是为了将灯光方向,以及视线方向转化到切线空间,然后利用光照方程进行计算。如果我们选择切线向量比较一致的情况下,对于不同顶点(或者说不同像素,他们是一一对应的)的不同切线空间坐标系下的灯光方向,视线方向差别很小。这样,利用这种特性,我们可以不必逐个计算纹素的坐标系(本身也不太可能),利用可编程流水线的插值功能来完成计算。例如一个被Normal Map映射的三角形,我们可以只在vertex shader中计算计算三个顶点各自的切线空间坐标系,从而得到三个顶点的切线空间下的灯光方向,视线方向的值,那么,直接作为varying变量丢给fragment shader,当然,流水线会对这些varying变量进行插值,也就是上图两幅的比较,我们追求的是两者尽可能的相等。
从以上可以看出,在切线空间下要比在摄像机或者世界坐标系下计算光照方程要更有效率。因为,不论如何,读取Normal Map中的数据只能在fragment shader中使用,那么将Normal Map中的向量转化为世界坐标系或者摄像机坐标系必然要使用矩阵来完成,注意到fragment shader是逐像素操作的,假如对于一个在屏幕上占300*300像素的正方形使用Normal Map,那么在fragment shader中就要进行90000次的矩阵运算。显然是很低效的。
而如果使用本文的介绍方法,对于只有四个顶点的正方形,只用计算四次矩阵转化,剩下的就是插值计算。所以,个人以为转化到切线空间是十分划算的。
本次探索收获很多,从以上分析可以看出,我们不仅更好的理解了流水线自带的坐标系,也学会如何自己创建坐标系以及如何高效的使用这些坐标系。并且,注意到一个对流水线一直忽略的特性:对于vertex shader的执行次数是和顶点数目相关的,执行完成后,varying 变量可以理解为和顶点绑定的数据 ,各种varying变量将会被插值传入fragmet shader中。fragment shader的执行次数和被映射到屏幕上的多变形占用的像素是正相关的。
具体代码稍后上传,也可以参考橙皮书的Bump Map章节。
如果文中有那些地方不正确,还希望大家指出。我也是图形学刚入门,希望得到大家的指点。
标签:
原文地址:http://www.cnblogs.com/BlackWalnut/p/4396920.html