标签:
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 3140 Accepted Submission(s): 1602
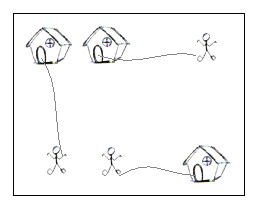 You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.
You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.
#include<iostream> #include<cstring> #include<climits> #include<queue> #include<cstdio> using namespace std; int abss(int a,int b) { if(a>b)return a-b; else return b-a; } struct MCMF { int cap,lf,flow,cost; }G[210][210]; char map[110][110]; int pre[210],dis[210]; bool isq[210]; struct House { int x,y; }house[110]; struct Man { int x,y; }man[110]; int n,m,home,people,all; void init() { home=people=0; for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { cin>>map[i][j]; if(map[i][j]==‘m‘) { man[++people].x=i; man[people].y=j; } else if(map[i][j]==‘H‘) { house[++home].x=i; house[home].y=j; } } } all=people+home+1; memset(G,0,sizeof(G)); for(int i=1;i<=people;i++) { G[0][i].cap=G[0][i].lf=1; for(int j=1;j<=home;j++) { G[i][j+people].cost=abss(man[i].x,house[j].x)+abss(man[i].y,house[j].y); G[j+people][i].cost=-G[i][j+people].cost; G[i][j+people].cap=G[i][j+people].lf=1; } G[i+people][all].cap=G[i+people][all].lf=1; } } void spfa(int s) { memset(pre,-1,sizeof(pre)); int temp; for(int i=0;i<=all;i++) { dis[i]=(i==s?0:INT_MAX); isq[i]=false; } queue<int>q; q.push(s); isq[s]=true; while(!q.empty()) { temp=q.front(); isq[temp]=false; q.pop(); for(int i=0;i<=all;i++) { if(G[temp][i].lf&&G[temp][i].cost+dis[temp]<dis[i]) { dis[i]=G[temp][i].cost+dis[temp]; pre[i]=temp; if(!isq[i]) { q.push(i); isq[i]=true; } } } } } void mcmf(int s,int t) { spfa(s); int sum=0; while(pre[t]!=-1) { int min=INT_MAX; for(int i=t;pre[i]!=-1;i=pre[i]) min=min<G[pre[i]][i].lf?min:G[pre[i]][i].lf; sum+=dis[t]; for(int i=t;pre[i]!=-1;i=pre[i]) { G[pre[i]][i].lf-=min; G[i][pre[i]].lf+=min; } spfa(s); } cout<<sum<<endl; } int main() { while(~scanf("%d%d",&n,&m),n+m) { init(); mcmf(0,all); } return 0; }
#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<climits> #include<algorithm> #include<queue> using namespace std; int n,m; const int N=250; const int M=10000; const int MAX=0xffffff; char coord[N][N];//坐标集 int pre[M];//存储前驱顶点 int dist[M];//存储到源点s的距离 int inq[M];//每个顶点是否在队列中的标志 int min_c_f;//记录增广路径中的残留容量 int vertex;//顶点数 int sum;//保存最小费用 struct element { int c;//容量 int f;//流 int c_f;//残留容量 int v;//价值 } G[N][N]; struct man//记录小矮人的坐标 { int x,y; } man[N]; struct house//记录房子的坐标 { int x,y; } house[N]; void init() { sum=0; int mcase,hcase;//记录有多少个小矮人和房子 mcase=hcase=0; for(int i=1; i<=m; i++)//输入过程 { for(int j=1; j<=n; j++) { cin>>coord[i][j]; if(coord[i][j]==‘m‘)//记录小矮人的坐标 { mcase++; man[mcase].x=i; man[mcase].y=j; } if(coord[i][j]==‘H‘)//记录房子的坐标 { hcase++; house[hcase].x=i; house[hcase].y=j; } } } vertex=mcase+hcase+1;//加入超源点0和超汇点,注意要+1,即抽象成网络流的结构 for(int u=0; u<=vertex; u++)//初始流为0,所以不用重构W(f); { for(int v=0; v<=vertex; v++) { G[u][v].c=G[v][u].c=0; G[u][v].c_f=G[v][u].c_f=0; G[u][v].f=G[v][u].f=0; G[u][v].v=G[v][u].v=MAX; } } for(int i=1; i<=mcase; i++) { G[0][i].v=0;//从超源点到各个小矮人之间的权值取为0 G[0][i].c=G[0][i].c_f=1;//从超源点到各个小矮人之间的容量取为1 for(int j=1; j<=hcase; j++) { int w=abs(house[j].x-man[i].x)+abs(house[j].y-man[i].y);//计算小矮人到每一个房子之间的距离 G[i][mcase+j].v=w;//将距离赋给对应的权值,注意第二个下标,即表示房子的下标为mcase+j~!! G[i][mcase+j].c=1;//容量取为1 G[i][mcase+j].c_f=G[i][mcase+j].c; G[mcase+j][vertex].v=0;//将从各个房子到超汇点之间的权值取为0,注意房子的下标为mcase+j G[mcase+j][vertex].c=G[mcase+j][vertex].c_f=1;//将从各个房子到超汇点之间的容量取为0,注意房子的下标为mcase+j } } } void SPFA(int s)//求最短路径的SPFA算法 { queue<int> Q; int u; for(int i=0; i<=vertex; i++)//初始化 { dist[i]=MAX; pre[i]=-1; inq[i]=0; } dist[s]=0; Q.push(s); inq[s] = 1; while(!Q.empty()) { u=Q.front(); Q.pop(); inq[u]=0; for(int i=0; i<=vertex; i++)//更新u的邻接点的dist[], pre[], inq[] { int v=i; if(G[u][v].c_f==0) // 表示(u,v)没有边 continue; if(G[u][v].v==MAX) G[u][v].v=-G[v][u].v; if(dist[v]>dist[u]+G[u][v].v)//松弛操作 { dist[v]=dist[u]+G[u][v].v; pre[v]=u; if(inq[v]==0) { Q.push(v); inq[v]=1; } } } } } void ford_fulkerson(int s,int t) { SPFA(s); while(pre[t]!=-1)//pre为-1表示没有找到从s到t的增广路径 { //cout<<dist[t]<<"^_^"<<endl; sum+=dist[t];//将这一条最短路径的值加进sum min_c_f=MAX; int u=pre[t], v=t;//计算增广路径上的残留容量 while(u!=-1) { if(min_c_f > G[u][v].c_f) min_c_f=G[u][v].c_f; v=u; u=pre[v]; } u=pre[t], v=t; while(u!=-1) { G[u][v].f+=min_c_f; //修改流 G[v][u].f=-G[u][v].f; G[u][v].c_f=G[u][v].c-G[u][v].f; //修改残留容量 G[v][u].c_f=G[v][u].c-G[v][u].f; v=u; u=pre[v]; } SPFA(s); } } int main() { while(cin>>m>>n,m||n) { init(); ford_fulkerson(0,vertex);//计算从超源点0到超汇点vertex之间的最小费用最大流 cout<<sum<<endl; } return 0; }
标签:
原文地址:http://www.cnblogs.com/lthb/p/4401520.html