标签:
欧几里得旅行商问题是一个NP问题,问题描述:平面上n个点,确定一条连接各点的最短闭合旅程。
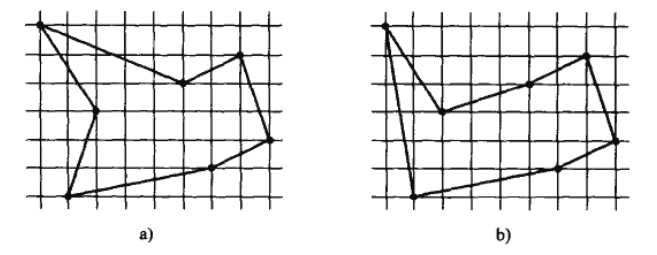
所以通常会简化为双调欧几里得问题来求一个近似解,借用下算法导论的图,如下所示
a)是一个最优欧几里得
b)为双调路线,从最左点开始严格向右至最右点
通过动态规划求解,首先需要分析子问题:
双调路径为 i -> 0,0 -> j; 最终结果为 i 和 j 都为n-1;所以子问题为0 <= i < n; 0 <= j < n;
由于存在对称情况(bitonic[i][j] == bitonic[j][i]),所以仅考虑 i 小于 j 的情况 即 0 <= i < j < n; i 为左调起点,j 为右调终点;
求解时要考虑一下三种情况
1)当 i < j - 1 时 , 由于i为左调曲线起点,所以j - 1, j都在右调曲线上
可以得出bitonic[i][j] = bitonic[i][j - 1] + distance[j - 1][j]
2)当 i == j - 1 时需要用到动态获取最小距离
foreach (0 < k < i)
bitonic[i][j] = min(bitonic[k][i] + distance[k][j])
3)当 i == j 时 由于线段p[j - 1][j]必定在左调或者右调线路上,
所以最优线路bitonic[j - 1][j]或bitonic[j][j - 1]即为最优 bitonic[j][j]的前置路线
因为bitonic[j - 1][j]和bitonic[j][j - 1]对称所以有:
bitonic[j][j] = bitonic[j - 1][j] + distance[j - 1][j]
分析好之后代码就很简单了:
package com.feinno.algorithmic.travelingsalesman; import java.util.Arrays; /** * 双调欧几里得算法 * bitonic[i][j] * 1)i为左调起点,j为右调终点 * 2)0 <= i <= j <= n * 当 i < j - 1 时 , 由于i为左调曲线起点,所以j - 1, j都在右调曲线上 * 可以得出bitonic[i][j] = bitonic[i][j - 1] + distance[j - 1][j] * 当 i == j - 1 时需要用到动态获取最小距离 * foreach (0 < k < i) * bitonic[i][j] = min(bitonic[k][i] + distance[k][j]) * 当 i == j 时 由于线段p[j - 1][j]必定在左调或者右调线路上, * 所以最优bitonic[j - 1][j]即为最优 bitonic[j][j]的前置路线 * bitonic[j][j] = bitonic[j - 1][j] + distance[j - 1][j] * * @author renzhaolong * */ public class BitonicTSP { /** * 两节点间距离 */ private double[][] distance; /** * 以i为左调起点,j为右调终点的双调距离 */ private double[][] bitonic; /** * 最优双调的前置节点 */ private Point[][] preposition; /** * 节点集合,按x坐标递增排序 */ private Point[] points; /** * 集合数量 */ int lenth = 0; /** * 按照约定计算双调欧几里得距离 * @return */ public double getBitonicResult() { bitonic[0][1] = getDistance(0, 1); for (int j = 2; j < lenth; j++) { // 第一种情况 i < j - 1 for (int i = 0; i < j - 1; i++) { bitonic[i][j] = bitonic[i][j - 1] + getDistance(j - 1, j); } //第二种情况i = j - 1 for (int k = 0; k < j - 1; k++) { double temp = bitonic[k][j - 1] + getDistance(k, j); if (temp < bitonic[j - 1][j]) { bitonic[j - 1][j] = temp; preposition[j - 1][j] = new Point(k, j - 1); } } } bitonic[lenth - 1][lenth - 1] = bitonic[lenth - 2][lenth - 1] + getDistance(lenth - 2, lenth - 1); return bitonic[lenth - 1][lenth - 1]; } /** * 获取两个节点的距离 * 如果缓存中存在数据直接返回,不存在计算并缓存 * @param x1 * @param x2 * @return */ private double getDistance(int x1, int x2) { if (x1 > x2) { x1 = x1 + x2; x2 = x1 - x2; x1 = x1 - x2; } if (distance[x1][x2] == -1) { distance[x1][x2] = points[x1].getDistance(points[x2]); } return distance[x1][x2]; } public BitonicTSP(Point[] points) { lenth = points.length; Arrays.sort(points); this.points = points; distance = new double[lenth][lenth]; bitonic = new double[lenth][lenth]; preposition = new Point[lenth][lenth]; for (int i = 0; i < lenth; i++) { for (int j = 0; j < lenth; j++) { distance[i][j] = -1; bitonic[i][j] = Double.MAX_VALUE; } } } public static void main(String[] args) { BitonicTSP tsp = new BitonicTSP( new Point[]{new Point(1, 1), new Point(2, 7), new Point(3, 4), new Point(6, 3), new Point(7, 6), new Point(8, 2), new Point(9, 5)}); System.out.println(tsp.getBitonicResult()); } }
package com.feinno.algorithmic.travelingsalesman; public class Point implements Comparable<Point> { private int x; private int y; public Point(int x, int y) { this.x = x; this.y = y; } public double getDistance(Point other) { return Math.sqrt(Math.pow(getX() - other.getX(), 2) + Math.pow(getY() - other.getY(), 2)); } public int getX() { return x; } public int getY() { return y; } @Override public int compareTo(Point o) { return getX() - o.getX(); } }
标签:
原文地址:http://www.cnblogs.com/remagon/p/4401605.html