标签：
先来说说‘树’（摘录自维基百科）：
在计算机科学中，树（英语：tree）是一种抽象资料型别（ADT）或是实作这种抽象资料型别的数据结构，用来模拟具树状结构性质的资料集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
‘二叉树’是‘树’的一种（摘录自维基百科）：
在计算机科学中，二叉树（英语：Binary tree）是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有
个结点；深度为k的二叉树至多有
个结点；对任何一棵二叉树T，如果其终端结点数为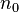
，度为2的结点数为
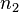，则
。
一棵深度为k，且有个节点称之为满二叉树；深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为完全二叉树。
与树不同，树的结点个数至少为1，而二叉树的结点个数可以为0；树中结点的最大度数没有限制，而二叉树结点的最大度数为2；树的结点无左、右之分，而二叉树的结点有左、右之分。
创建个二叉树：
/* 二叉樹的二叉鏈表存儲表示 */
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; /* 左右孩子指針 */
}BiTNode,*BiTree;
//按先序序列创建二叉树 int CreateBiTree(BiTree &T){ char data; //按先序次序输入二叉树中结点的值（一个字符），‘#’表示空树 scanf("%c",&data); if(data == ‘#‘){ T = NULL; } else{ T = (BiTree)malloc(sizeof(BiTNode)); //生成根结点 T->data = data; //构造左子树 CreateBiTree(T->lchild); //构造右子树 CreateBiTree(T->rchild); } return 0; }
其中有关二叉树的遍历（先访问左子树）：分为前（根）序遍历，中（根）序遍历，后（根）序遍历
假设用L（左子树指针）D（数据域，即根）R（右子树指针）来表示二叉树：
1、前（根）序遍历：
可表示为DLR，文字表达为
（1）访问根节点，
（2）访问左子树，
（3）访问右子树。
void PreOrderTraverse(BiTree T) { if(T) { Visit(T); PreOrderTraverse(T->lchild); PreOrderTraverse(T->rchild); } }
2、中（根）序遍历：
可表示为LDR，文字表达为
（1）访问左子树，
（2）访问根节点，
（3）访问右子树。
void MidOrderTraverse(BiTree T) { if(T) { MidOrderTraverse(T->lchild); Visit(T); MidOrderTraverse(T->rchild); } }
3、后（根）序遍历：
可表示为RLD，文字表达为
（1）访问左子树，
（2）访问右子树，
（3）访问根节点。
void RearOrderTraverse(BiTree T) { if(T) { RearOrderTraverse(T->lchild); RearOrderTraverse(T->rchild); Visit(T); } }
标签：
原文地址：http://www.cnblogs.com/omenglvrong1/p/4408770.html
