标签:
1. URM-Computable Functions
URM is short for Unlimited Register Machine, which is a computation model conceived by Shepherdson & Sturgis.
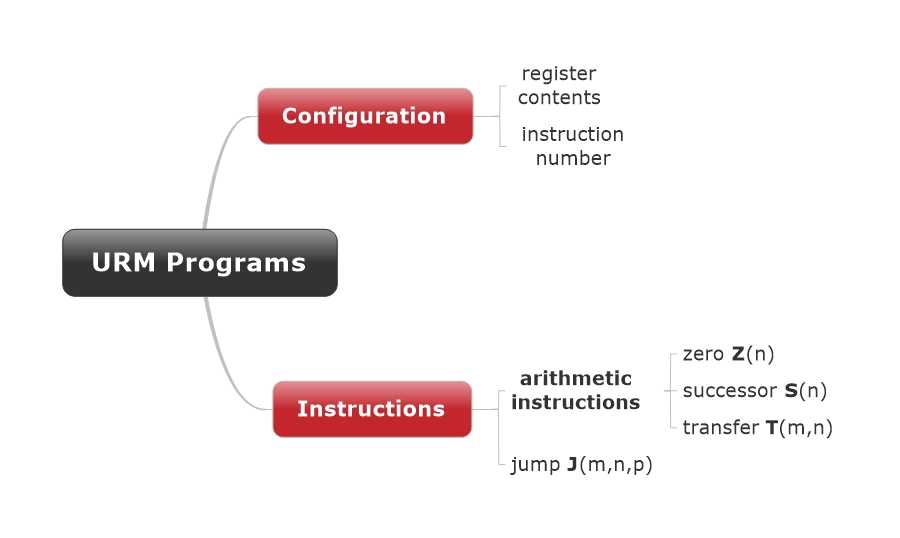
The function f is URM-computable iff there exists a program that URM-computes f.
2. Recursive Functions
Partial Recursive Functions is a set of computable functions defined by Gödel and Kleene in 1936.
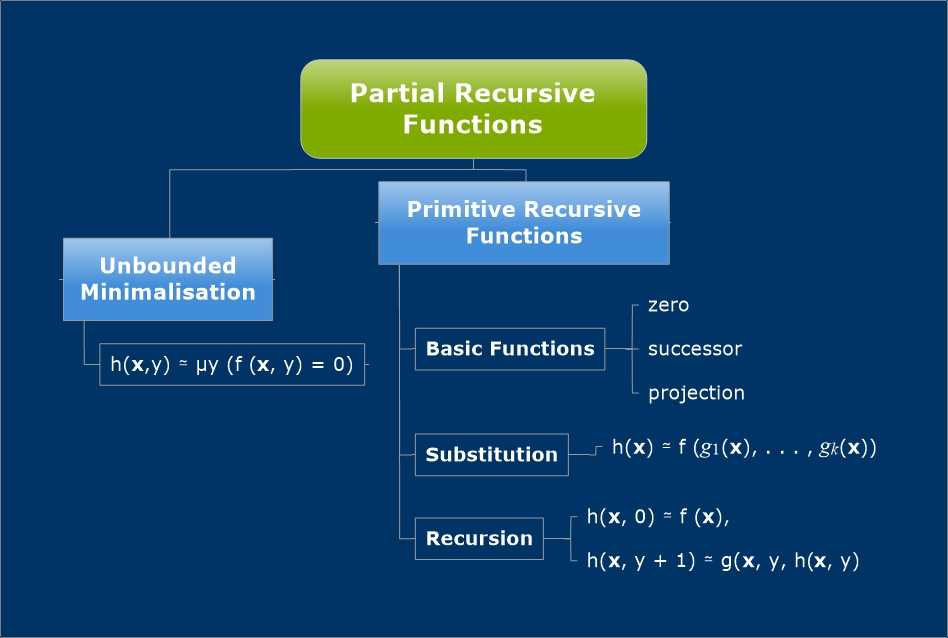
As an example, Ackerman Function defined as follow is a partial recursive function, but not a primitive recursive function.
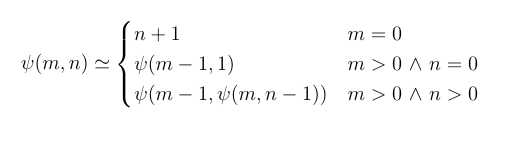
A predicate is decidable iff its characteristic function is recursive.
3. Turing-Computable Functions
The three fundamental components of a multi-tape Turing Machine are an Alphabet (a finite set of symbols), a finite set of States and a Transfer Function.
The computation ability of a Turing Machine does not vary with its size of alphabet, its number of tapes, or whether its tapes are unidirectional or bidirectional.
It can be proved that: URM-Computable Functions = Partial Recursive Functions = Turing-Computable Functions
4. Church‘s Thesis
The intuitively and informally defined class of effectively computable partial functions coincide exactly with the class of URM-computable functions.
References:
1. Cutland, Nigel. Computability: an introduction to recursive function theory[M]. Cambridge: Cambridge University Press, 1980
标签:
原文地址:http://www.cnblogs.com/DevinZ/p/4418351.html