【矩阵快速幂 】Codeforces 450B - Jzzhu and Sequences （公式转化）

标签：矩阵快速幂 acm

【题目链接】click here~~

【题目大意】

Jzzhu has invented a kind of sequences, they meet the following property:

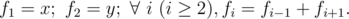
You are given x and y, please calculate f_n modulo1000000007(10⁹?+?7).

/*A - Jzzhu and Sequences
Codeforces 450B - Jzzhu and Sequences ( 矩阵快速幂 )
给定f1和f2，求fn
分析:
特判f1,f2
当n>=3时使用矩阵快速幂即可
将公式转化一下 , 可以得到一个变换矩阵
由F(i)=F(i-1)+F(i+1);
 将左式移到右边得
  F(i+i)=F(i)-F(i-1);
下标同时减一得
  F(i)=F(i-1)-F(i-2);
从而构造矩阵
(F(i-1),F(i-2))*[1 -1 ]=(F(i),F(i-1))
                [1  0 ]
带入i=3,得
(F(2)=y,F(1)=x)*[1 -1 ]^(i-2)=(F(3),F(2))
                [1  0 ]
代码如下*/

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
const long long  MOD=1e9+7;
#define LL long long
struct Matrlc
{
    long long  mapp[2][2];
} ans,base;
Matrlc unit={1,0,0,1};
Matrlc mult(Matrlc a,Matrlc b)
{
    Matrlc c;
    for(int i=0; i<2; i++)
        for(int j=0; j<2; j++)
        {
            c.mapp[i][j]=0;
            for(int k=0; k<2; k++)
                c.mapp[i][j]+=(a.mapp[i][k]*b.mapp[k][j])%MOD;
                c.mapp[i][j]%=MOD;
        }
    return c;
}
void pow1(LL n)
{
    base.mapp[0][0] =1;
    base.mapp[0][1] = -1;
    base.mapp[1][0] = 1;
    base.mapp[1][1] = 0;
    ans.mapp[0][0] = ans.mapp[1][1] = 1;// ans 初始化为单位矩阵
    ans.mapp[0][1] = ans.mapp[1][0] = 0;
    while(n)
    {
        if(n&1)   ans=mult(ans,base);
        base=mult(base,base);
        n>>=1;
    }
}
int main()
{
    LL X,Y,N,i,j;
    scanf("%lld%lld%lld",&X,&Y,&N);
    if(N==1) printf("%lld\n",(X%MOD+MOD)%MOD);
    else if(N==2) printf("%lld\n",(Y%MOD+MOD)%MOD);
    else
    {
        pow1(N-2);
        LL  result=(((ans.mapp[0][0]*Y+ans.mapp[0][1]*X)%MOD)+MOD)%MOD;
        printf("%lld\n",result);
    }
    return 0;
}

【矩阵快速幂 】Codeforces 450B - Jzzhu and Sequences （公式转化）

标签：矩阵快速幂 acm

原文地址：http://blog.csdn.net/u013050857/article/details/44998799