题目
骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
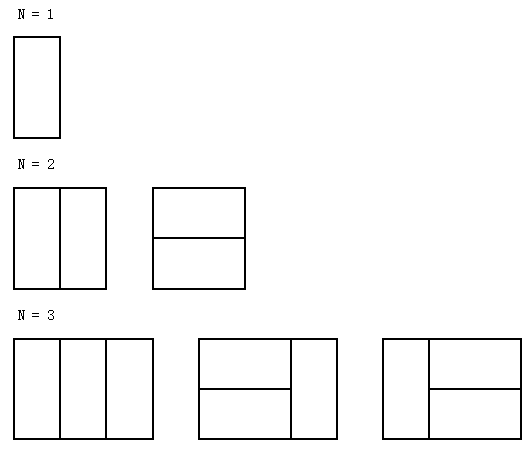
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：
62247088
17748018
前面几组一写，，很容易就能发现规律，是一个线性递推，甚至就是斐波那契。那么下面就是解决巨大斐波那契取模的问题了。
提示：如何快速计算结果
当N很小的时候，我们直接通过递推公式便可以计算。当N很大的时候，只要我们的电脑足够好，我们仍然可以直接通过递推公式来计算。
但是我们学算法的，总是这样直接枚举不是显得很Low么，所以我们要用一个好的算法来加速(装X)。
事实上，对于这种线性递推式，我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列，我们希望找到一个2x2的矩阵M，使得(a, b) x M = (b, a+b)，其中(a, b)和(b, a+b)都是1x2的矩阵。
显然，只需要取M = [0, 1; 1, 1]就可以了：
代码：
#include <iostream>
#include<stdio.h>
#include<mem.h>
using namespace std;
const int MAXN=4;
const int MAXM=4;
const int MOD=19999997;
struct Matrix
{
long long int n,m;
long long int a[MAXN][MAXM];
void clear()
{
n=m=0;
memset(a,0,sizeof(a));
}
Matrix operator +(const Matrix &b)const
{
Matrix tmp;
tmp.n=n;
tmp.m=m;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
{
tmp.a[i][j]=(a[i][j]+b.a[i][j])%MOD;
}
return tmp;
}
Matrix operator -(const Matrix &b)const
{
Matrix tmp;
tmp.n=n;
tmp.m=m;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
tmp.a[i][j]=(a[i][j]-b.a[i][j])%MOD;
return tmp;
}
Matrix operator *(const Matrix &b)const
{
Matrix tmp;
tmp.clear();
tmp.n=n;
tmp.m=m;
for(int i=0;i<n;++i)
{
for(int j=0;j<m;++j)
{
for(int k=0;k<m;++k)
{
tmp.a[i][j]=(tmp.a[i][j]+(a[i][k]*b.a[k][j])%MOD)%MOD;
}
}
}
return tmp;
}
};
int solve(int a[],int b[],int n,int t)
{
Matrix M,F,E;
M.clear();
F.clear();
E.clear();
M.n=M.m=n;
E.n=E.m=n;
F.n=n;
F.m=1;
for(int i=0;i<n-1;++i)
{
M.a[i][i+1]=1;
}
for(int i=0;i<n;i++)
{
M.a[n-1][i]=a[i];
F.a[i][0]=b[i];
E.a[i][i]=1;
}
if(t<n)
return F.a[t][0];
for(t-=n-1;t;t/=2)
{
if(t&1)
E=M*E;
M=M*M;
}
F=E*F;
return F.a[n-1][0];
}
int main()
{
int a[]={1,1};
int b[]={1,2};
int n=2;
int t;
cin>>t;
cout<<solve(a,b,n,t-1)%MOD<<endl;
return 0;
}
之所以wa了一炮是因为本地跑的时候用的<mem.h>,网站上的G++不认，要用<memory.h>
原文地址：http://blog.csdn.net/xiaopangxia/article/details/45021885
