标签:
伸展树是一种平衡二叉树。在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。
平衡二叉树都需要通过旋转操作来维持树的平衡性.
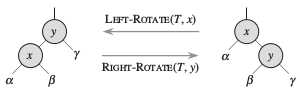
Left_Rotate(T,x)//x.right ≠ NIL y = x.right // set y x.right = y.left //turn y‘s left subtree to x‘s right subtree if y.left ≠ NIL y.left.p = x y.p = x.p //link x‘s parent to y if x.p == NIL T.root = y else if x == x.p.left x.p.left = y else x.p.right = y y.left = x //put x on y‘s left x.p = y Right_Rotate(T,y)//y.left ≠ NIL x = y.left // set x y.left = x.right //turn x‘s right subtree to y‘s left subtree if x.right ≠ NIL x.right.p = y x.p = y.p //link y‘s parent to x if y.p == NIL T.root = x else if y == y.p.left y.p.left = x else y.p.right = x x.right = y //put y on x‘s right y.p = x
伸展操作:
void splay( node *x ) { while( x->parent ) { if( !x->parent->parent ) {//x的父结点为树根 if( x->parent->left == x ) right_rotate( x->parent ); else left_rotate( x->parent ); } else if( x->parent->left == x && x->parent->parent->left == x->parent ) {//左"一字型" right_rotate( x->parent->parent ); right_rotate( x->parent ); } else if( x->parent->right == x && x->parent->parent->right == x->parent ) {//右"一字型" left_rotate( x->parent->parent ); left_rotate( x->parent ); } else if( x->parent->left == x && x->parent->parent->right == x->parent ) {//左右"之自型"(从下至上看) right_rotate( x->parent ); left_rotate( x->parent ); } else {//右左"之自型"(从下至上看) left_rotate( x->parent ); right_rotate( x->parent ); } } }

标签:
原文地址:http://www.cnblogs.com/bukekangli/p/4421936.html