题意 求费波拉契数列第N项 1≤N≤100,000,000
通过矩阵的幂 可以把一维递推的时间复杂度减小到O(logN) 主要就是快速幂的思想
对于m^n 若n=2^a1+2^a2+...+2^ak 那么m^n = m^(2^a1) * m^(2^a2) * ... * m^(2^ak) 那么只用看n转换为二进制后哪些位为1就可以快速求出m^n了
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2;
const LL MOD = 19999997;
//将矩阵a*b的结果放入c
void matMul(LL a[][N], LL b[][N], LL c[][N])
{
LL ret[N][N] = {0};
for(int i = 0; i < N; ++i)
for(int j = 0; j < N; ++j)
for(int k = 0; k < N; ++k)
ret[i][j] = (ret[i][j] + a[i][k] * b[k][j]) % MOD;
for(int i = 0; i < N; ++i)
memcpy(c[i], ret[i], sizeof(c[i]));
}
//将a^n放入a
void matPow(LL a[][N], int n)
{
LL ret[N][N] = {0};
for(int i = 0; i < N; ++i) ret[i][i] = 1;
while(n)
{
if(n & 1) matMul(ret, a, ret);
matMul(a, a, a);
n >>= 1;
}
for(int i = 0; i < N; ++i)
memcpy(a[i], ret[i], sizeof(a[i]));
}
int main()
{
int n;
while(~scanf("%d", &n))
{
LL a[N][N] = {0, 1, 1, 1};
matPow(a, n);
printf("%lld\n", a[1][1] % MOD);
}
return 0;
}
骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题:
我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
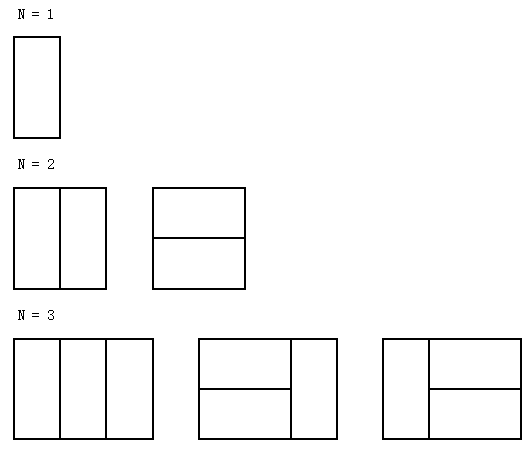
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
第1行:1个整数,表示覆盖方案数 MOD 19999997
62247088
17748018
hiho一下·41 骨牌覆盖问题·一(矩阵快速幂·费波拉契)
原文地址:http://blog.csdn.net/acvay/article/details/45028667