标签:
比赛链接: here
题目对应到ZOJ3860~3868
水

#include<cstdio> #include<map> #include<cstring> #include<iostream> using namespace std; map<int,int>mp; map<int,int>::iterator it; int main() { int T,n,x; scanf("%d",&T); while(T--) { mp.clear(); scanf("%d",&n); for(int i=0;i<n;i++) { scanf("%d",&x); mp[x]++; } for(it=mp.begin();it!=mp.end();it++) { if(it->second==1)printf("%d\n",it->first); } } return 0; }
水 dfs
3*3的九宫格,给你其中n个点按下面要求连起来:
1. 给你的n个点都要激活(至少经过一次)
2. 如果点A,B相连后要经过另一个点C,则C在序列中的位置必须在A,B之前 如 1 7 4是不合法的
3.线段相交是没关系的,如 7 6 9 4
A B线段中有点C的情况
1. AB行号相差2并且列号一样 C=(A+B)/2
2.AB列号相差2并且行号一样 C=(A+B)/2
3.AB行号和列号都相差2(对角)C=(A+B)/2
由于要多次用到abs运算和行列号的运算,可以先把运算结果存起来

#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; int x[10],y[10]; int re[5][5]; int a[10]; int n; bool vis[10]; int cnt; int s[10]; void dfs(int pre,int num,int op) { // printf("%d %d\n",pre,num); int i,t; if(num==n) { if(op){ for(i=0;i<n-1;i++)printf("%d ",s[i]); printf("%d\n",s[n-1]); } cnt++; return; } for(i=0;i<n;i++) { if(!vis[a[i]]) { if(re[x[a[i]]][x[pre]]==2||re[y[a[i]]][y[pre]]==2) { t=(pre+a[i])>>1; if(vis[t]) { vis[a[i]]=true; s[num]=a[i]; dfs(a[i],num+1,op); vis[a[i]]=false; } } else { vis[a[i]]=true; s[num]=a[i]; dfs(a[i],num+1,op); vis[a[i]]=false; } } } } int main() { int T,i,j; for(i=1;i<10;i++)x[i]=(i-1)/3; for(i=1;i<10;i++)y[i]=(i-1)%3; for(i=0;i<3;i++) { for(j=0;j<3;j++) re[i][j]=abs(i-j); } scanf("%d",&T); while(T--) { scanf("%d",&n); for(i=0;i<n;i++){ scanf("%d",&a[i]); } sort(a,a+n); cnt=0; for(i=0;i<n;i++){ memset(vis,false,sizeof(vis)); vis[a[i]]=true; s[0]=a[i]; dfs(a[i],1,0); } printf("%d\n",cnt); for(i=0;i<n;i++){ memset(vis,false,sizeof(vis)); vis[a[i]]=true; s[0]=a[i]; dfs(a[i],1,1); } } return 0; }
看了解题报告后发现这题也是水题
题意:
按1-2n的编号给定2n个点以及n条线段,每个点属于且仅属于一条线段。
线段用端点的编号确定。
现在一次操作可以交换两个点的编号,
要求在不超过n+10次的操作后使得任意两条线段不相交。
输入保证任意两个点不重合,任意三个点不相交。
思路:
首先要明确,不是要求最少操作次数,只要不超过n+10次就可以。
所以一定有解:
step 1: 点配对
把所有点按水平序排好,人为配对:排名2k-1的点和排名2k的点组成一条线段。(2k-1并不是点的编号,只是排序后的位置)
这样的话没有线段会相交。
step 2: 统计操作次数
点已经配好了,只要计算从原来的配对变成现在的配对需要多少次操作。
假设排序后的点编号是:a, b, ... , c, ... , d , ....
本来是a和c组成一条线段,b和d组成一条线段
为了让a和c配对,交换b和c的编号(其实是交换b和c对应的点坐标。。。)
显然最多进行n次操作
把握一点:操作之后,点的编号对应关系不变。
比如说1号点一开始与4号点组成线段,操作之后还是1号点和4号点组成线段
但是1号点和4号点的坐标可能和之前不一样
理解这一点就好了。。。

#include<iostream> #include<cstdio> #include<vector> #include<algorithm> using namespace std; #define maxn 200020 struct ss { int x, y ,id; ss(){} ss(int _x,int _y):x(_x),y(_y){} }p[maxn]; int f[maxn]; int rk[maxn]; int n; bool cmp(ss a,ss b) { if(a.x==b.x)return a.y<b.y; return a.x<b.x; } vector<ss>v; int main() { int T; scanf("%d",&T); while(T--) { v.clear(); scanf("%d",&n); for(int i=1;i<=2*n;i++){ scanf("%d%d",&p[i].x,&p[i].y); p[i].id=i; } int a,b; for(int i=1;i<=n;i++) { scanf("%d%d",&a,&b); f[a]=b;f[b]=a; } sort(p+1,p+2*n+1,cmp); for(int i=1;i<=2*n;i++){ rk[p[i].id]=i; } for(int i=1;i<=2*n;i+=2){ int a=p[i].id,b=p[i+1].id; if(f[a]!=b) { int c=f[a],d=f[b]; v.push_back(ss(b,c)); swap(p[i+1].id,p[rk[c]].id); swap(rk[b],rk[c]); } } printf("%d\n",v.size()); for(int i=0;i<v.size();i++) { printf("%d %d\n",v[i].x,v[i].y); } } return 0; }
鸟神的极角排序代码:
极角排序后相邻的两点为一组

#include <stdio.h> #include <algorithm> #include <string.h> #include <queue> #include <math.h> #include <string> #include <vector> using namespace std; #define rep( i , a , b ) for ( int i = ( a ) ; i < ( b ) ; ++ i ) #define For( i , a , b ) for ( int i = ( a ) ; i <= ( b ) ; ++ i ) #define rev( i , a , b ) for ( int i = ( a ) ; i >= ( b ) ; -- i ) #define clr( a , x ) memset ( a , x , sizeof a ) const int MAXN = 200005 ; struct Point { int x , y , idx ; double r ; Point () {} Point ( int x , int y ) : x ( x ) , y ( y ) {} bool operator < ( const Point& a ) const { return r < a.r ; } } ; struct Node { int x , y ; Node () {} Node ( int x , int y ) : x ( x ) , y ( y ) {} } ; Point p[MAXN] ; int idx[MAXN] ; int idxf[MAXN] ; Node q[MAXN] ; Node ans[MAXN] ; int top ; int n ; bool cmp ( const Point& a , const Point& b ) { return a.idx < b.idx ; } void solve () { int x , y ; top = 0 ; scanf ( "%d" , &n ) ; rep ( i , 0 , 2 * n ) { scanf ( "%d%d" , &p[i].x , &p[i].y ) ; p[i].x += 1e9 ; p[i].y += 1e9 ; p[i].r = atan2 ( p[i].y , p[i].x ) ; p[i].idx = i ; } sort ( p , p + 2 * n ) ; rep ( i , 0 , 2 * n ) { idx[p[i].idx] = i ; idxf[i] = p[i].idx ; } //rep ( i , 0 , 2 * n ) printf ( "---%d %d %d %d\n" , p[i].idx , i , idx[p[i].idx] , idxf[i] ) ; sort ( p , p + 2 * n , cmp ) ; For ( i , 1 , n ) { scanf ( "%d%d" , &x , &y ) ; -- x ; -- y ; x = p[x].idx ; y = p[y].idx ; //printf ( "%d %d\n" , x , y ) ; int xx = idx[x] % 2 ; int yy = idx[y] % 2 ; //printf ( "xx = %d yy = %d\n" , idx[x] , idx[y] ) ; int t ; if ( !xx && idx[x] + 1 == idx[y] || xx && idx[x] - 1 == idx[y] ) continue ; if ( !xx ) t = idx[x] + 1 ; else t = idx[x] - 1 ; //printf ( "------------%d %d\n" , y , t ) ; ans[++ top] = Node ( y , idxf[t] ) ; int tmp = idx[y] ; swap ( idx[y] , idx[idxf[t]] ) ; swap ( idxf[tmp] , idxf[t] ) ; //printf ( "%d %d\n" , idxf[idx[x]] , idxf[idx[y]] ) ; } printf ( "%d\n" , top ) ; For ( i , 1 , top ) printf ( "%d %d\n" , ans[i].x + 1 , ans[i].y + 1 ) ; } int main () { int T ; scanf ( "%d", &T ) ; For ( i , 1 , T ) solve () ; return 0 ; }
留个坑!!!!待填。
水题 dfs 比赛时没时间看
就是求连通块的个数,把每种图像的黑色块个数和白色块个数数出来就行了
其中Sehun,Xiumin 黑色块为5 ,白块为2 一样,则用面积比(最大黑色块:最小黑色块来判断)
注意900*900=810000,早就暴栈了,手动扩展也没用!dfs时用队列存储状态即可。

#include<iostream> #include<cstdio> #include<queue> #include<cstring> using namespace std; int mp[1000][1000]; int n,m; int s[2]; bool vis[1000][1000]; int dx[9]={-1,-1,-1,0,0,1,1,1}; int dy[9]={-1,0,1,-1,1,-1,0,1}; int sum,mini,maxi; queue<pair<int,int> >q; void dfs(int x,int y,int op) { while(!q.empty())q.pop(); q.push(make_pair(x,y)); vis[x][y]=true; while(!q.empty()) { int xx,yy; x=q.front().first; y=q.front().second; q.pop(); sum++; for(int i=0;i<8;i++) { xx=x+dx[i]; yy=y+dy[i]; if(xx>=0&&xx<n&&yy>=0&&yy<n&&mp[xx][yy]==op&&!vis[xx][yy]) { q.push(make_pair(xx,yy)); vis[xx][yy]=true; } } } } int main() { int T; scanf("%d",&T); while(T--) { int flag=1; int x,id=0; scanf("%d%d",&n,&m); while(m--) { scanf("%d",&x); while(x--) { mp[id/n][id%n]=flag; id++; } flag=!flag; } s[0]=0; memset(vis,false,sizeof(vis)); mini=100000;maxi=0; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(mp[i][j]==0&&!vis[i][j]){ s[0]++; sum=0; dfs(i,j,0); if(sum<mini)mini=sum; if(sum>maxi)maxi=sum; } } } s[1]=0; memset(vis,false,sizeof(vis)); for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(mp[i][j]==1&&!vis[i][j]){ s[1]++; dfs(i,j,1); } } } if(s[0]==9&&s[1]==2)puts("Baekhyun"); if(s[0]==5&&s[1]==1)puts("Chanyeol"); if(s[0]==1&&s[1]==3)puts("Chen"); if(s[0]==1&&s[1]==2)puts("D.O"); if(s[0]==2&&s[1]==13)puts("Kai"); if(s[0]==3&&s[1]==1)puts("Kris"); if(s[0]==6&&s[1]==2)puts("Lay"); if(s[0]==5&&s[1]==8)puts("Luhan"); if(s[0]==2&&s[1]==8)puts("Suho"); if(s[0]==2&&s[1]==4)puts("Tao"); if(s[0]==5&&s[1]==2){ if(mini*20<maxi)puts("Sehun"); else puts("Xiumin"); } } return 0; } /* 2 6 13 7 2 1 1 2 3 4 1 4 1 1 2 7 ca1 131 1194 ca2 53 1646 */
水 bfs
只不过状态用vis[20][20][4]来记录,每个点都有四个状态,访问过就不能访问
通过控制面板控制机器人找钻石,控制面板每p时间右移一次(队尾变队首),求最短路径
控制面板为左右上下的顺序,初始时 光标在左
有3种操作,占用一个单位时间
1. 光标左移(最左的移到最右)或者右移(最右的移到最左)
2.按按钮,机器人会根据光标所指的方向移动一个单位
3.停在原地

#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<algorithm> using namespace std; int n,m,p; char mp[20][20]; int sx,sy,ex,ey; //l(0) r(1) u(2) d(3) int dx[4]={0,0,-1,1}; int dy[4]={-1,1,0,0}; bool vis[20][20][4]; struct ss { int x,y; int step; int dir; ss(){} ss(int _x,int _y,int _step,int _dir):x(_x),y(_y),step(_step),dir(_dir){} }t; queue<ss>q; void bfs() { int x,y,step,dir,time; while(!q.empty())q.pop(); t=ss(sx,sy,0,0); q.push(t); while(!q.empty()) { t=q.front(); q.pop(); if(t.x==ex&&t.y==ey) { printf("%d\n",t.step); return; } if(t.step&&t.step%p==0) { t.dir=(t.dir+3)%4; } if(vis[t.x][t.y][t.dir])continue; vis[t.x][t.y][t.dir]=true; x=t.x+dx[t.dir]; y=t.y+dy[t.dir]; step=t.step+1; dir=t.dir; if(x>=0&&x<n&&y>=0&&y<m&&mp[x][y]!=‘*‘) { q.push(ss(x,y,step,dir)); } x=t.x; y=t.y; step=t.step+1; dir=t.dir; q.push(ss(x,y,step,dir)); x=t.x; y=t.y; step=t.step+1; dir=(t.dir+1)%4; q.push(ss(x,y,step,dir)); x=t.x; y=t.y; step=t.step+1; dir=(t.dir+3)%4; q.push(ss(x,y,step,dir)); } puts("YouBadbad"); } int main() { int T; scanf("%d",&T); while(T--) { int i,j; scanf("%d%d%d",&n,&m,&p); for(i=0;i<n;i++){ scanf("%s",mp[i]); for(j=0;j<m;j++) { if(mp[i][j]==‘@‘) { sx=i; sy=j; } else if(mp[i][j]==‘$‘) { ex=i; ey=j; } } } memset(vis,false,sizeof(vis)); bfs(); } return 0; }
几何体,留个坑!!!!待填。
先把公式存着以后慢慢推
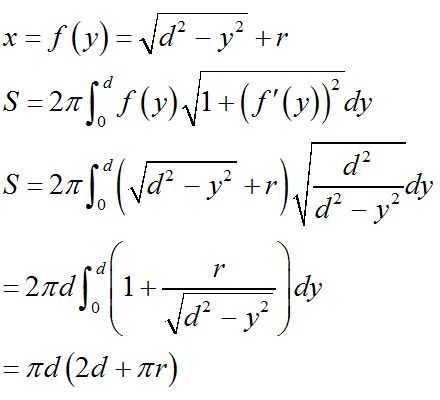
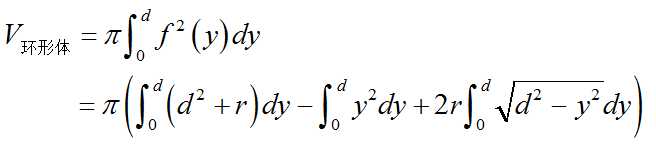
水

#include<iostream> #include<cstdio> #include<vector> #include<map> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<queue> #include<stack> #include<cstdlib> using namespace std; const int maxn=22222; const int inf=9999999999; int main() { int t; cin>>t; while(t--) { int a,b,A,B; cin>>a>>b>>A>>B; if(a==0) {cout<<"Invalid"<<endl;continue;} b=b-A; B=B-a; if(b<=0&&B>0) cout<<"Discard"<<" "<<A<<" "<<B<<endl; else if(b>0&&B<=0) cout<<a<<" "<<b<<" Discard"<<endl; else if(b>0&&B>0)cout<<a<<" "<<b<<" "<<A<<" "<<B<<endl; else cout<<"Discard Discard"<<endl; } return 0; }
脑洞题
暴力统计。
比如用dp[i] 表示gcd为i的子集个数。
那么如果i的倍数有x个, 那么gcd为 i的倍数的子集个数就是 2^x - 1。
要算gcd恰好为i的,那么就减掉就好。
dp[i] = 2^x - 1; for(int j = i+i;j <= Max;j += i) dp[i] -= dp[j];
倒过来求dp[i]就好。 复杂度就是调和级数的复杂度nln n.
简单题啊。

#include<iostream> #include<cstdio> #include<cmath> #include<cstring> using namespace std; #define maxn 1000010 #define mod 998244353 #define ll long long int a[maxn]; ll dp[maxn]; ll b[maxn]; ll pow_m(ll a,ll n) { ll ret=1; ll tmp=a; while(n) { if(n&1)ret=ret*tmp%mod; tmp=tmp*tmp%mod; n>>=1; } return ret; } int main() { int n,k,T; scanf("%d",&T); while(T--) { memset(b,0,sizeof(b)); scanf("%d%d",&n,&k); int ma=0; for(int i=0;i<n;i++){ scanf("%d",&a[i]); ma=max(ma,a[i]); b[a[i]]++; } ll ans=0; for(int i=ma;i>=1;i--) { dp[i]=0; ll cc=0; for(int j=i;j<=ma;j+=i) { cc+=b[j]; if(j>i)dp[i]=(dp[i]-dp[j]+mod)%mod; } dp[i]=(dp[i]+pow_m(2,cc)-1)%mod; //printf("%d %d\n",i,dp[i]); ans+=dp[i]*pow_m(i,k)%mod; ans%=mod; } printf("%lld\n",ans); } return 0; }
标签:
原文地址:http://www.cnblogs.com/kylehz/p/4420009.html