标签:
线性结构、树型结构、图状结构和纯集合结构作为数据的四种结构,树型结构是一类重要的非线性结构。
以二叉树为例了解一下树型结构的基本性质及用法:
二叉树:
每个节点至多有两棵子树,左子树和右子树,次序不可颠倒
非空二叉树的第n层至多有2^(n-1)个结点
深度为h的二叉树至多有2^h - 1 个结点
完美二叉树(满二叉树)的结点个数为2^h - 1
完全二叉树的第h层的结点都集中在左边
完美二叉树本身也是完全二叉树
对于完全二叉树,设一个结点(非根结点)编号为 i ,则其父亲结点编号为 i / 2 , 其左子结点编号为 2 * i , 右子结点编号为 2 * i + 1
叶子结点的个数等于度为2的结点个数 + 1
同理:
m叉树的叶子结点个数n0,有一个儿子的结点个数n1,有两个儿子的结点个数n2,有三个儿子的结点个数n3……有m个儿子的结点个nm之间存在什么关系?
n0 + n1 + n2 + …… nm - 1 = 0 * n0 + 1 * n1 + 2 * n2 + 3 * n3 + 4 * n4 + …… m * nm
所以: n0 - 1 = n2 + 2 * n3 + 3 * n4 + …… + (m-1) * nm
存储结构:
顺序存储:
完全二叉树可以用数组来实现,一般二叉树如果采用这种存储方式,空间代价较高
数组实现二叉树的顺序存储代码:
typedef struct Node { int data ; int lchild , rchild ; int father ; }Node ; Node btree[1000] ;
链式存储:
typedef struct Node { int data ; struct Node * lchild ; struct Node * rchild ; }Node ; Node *new_Node() { Node * newnode = new Node ; newnode->data = 0 ; newnode->lchild = NULL ; newnode->rchild = NULL ; return newnode ; }
二叉树的遍历:
遍历即二叉树的所有结点访问一遍,根据访问根结点的顺序分为:先序遍历、中序遍历和后续遍历:
先序遍历: 根结点 -> 左子树 -> 右子树
中序遍历: 左子树 -> 根结点 -> 右子树
后序遍历: 左子树 -> 右子树 -> 根结点
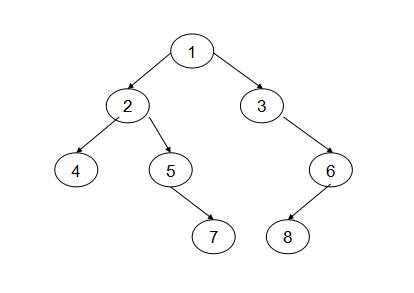
先序遍历:1 -> 2 -> 4 -> 5 -> 7 -> 3 -> 6 -> 8
中序遍历:4 -> 2 -> 5 -> 7 -> 1 -> 3 -> 8 -> 6
后序遍历:4 -> 7 -> 5 -> 2 -> 8 -> 6 -> 3 -> 1
遍历的递归实现:
#include<iostream> #include<stdio.h> using namespace std ; typedef struct Node { int data ; struct Node * lchild ; struct Node * rchild ; }Node ; Node *new_Node() { Node * newnode = new Node ; newnode->data = 0 ; newnode->lchild = NULL ; newnode->rchild = NULL ; return newnode ; } typedef Node *node ; Node *CreatebinTree() { int a ; Node *T ; cin >> a ; if(a == 0) return NULL ; else { T = new_Node() ; T->data = a ; T->lchild = CreatebinTree() ; T->rchild = CreatebinTree() ; } return T ; } void preorder(node T) { if(T) { if(T->data != 0) cout << T->data << " " ; preorder(T->lchild) ; preorder(T->rchild) ; } } int main() { freopen("in.txt","r",stdin) ; Node * root = CreatebinTree() ; preorder(root) ; return 0 ; } // 输入数据: // 1 2 4 0 0 5 0 7 0 0 3 0 6 8 0 0 0
标签:
原文地址:http://www.cnblogs.com/scottdinggo/p/4423394.html