SIFT特征描述子是David G. Lowe 在2004年的ijcv会议上发表的论文中提出来的，论文名为<<Distinctive Image Featuresfrom Scale-Invariant Keypoints>>。这是一个很强大的算法，主要用于图像配准和物体识别等领域，但是其计算量相比也比较大，性价比比较高的算法包括PCA-SIFT和SURF，其中OpenCV提供了SURF算法，OpenCV2.3版本后的SIFT算法是Rob Hess的源码，github的项目地址是http://blogs.oregonstate.edu/hess/code/sift/
SIFT特征描述子的优点：
int sift_features( IplImage* img, struct feature** feat )
{
return _sift_features( img, feat, SIFT_INTVLS, SIFT_SIGMA, SIFT_CONTR_THR,
SIFT_CURV_THR, SIFT_IMG_DBL, SIFT_DESCR_WIDTH,
SIFT_DESCR_HIST_BINS );
}
struct feature
{
double x; /**< x coord */
double y; /**< y coord */
double a; /**< Oxford-type affine region parameter */
double b; /**< Oxford-type affine region parameter */
double c; /**< Oxford-type affine region parameter */
double scl; /**< scale of a Lowe-style feature */
double ori; /**< orientation of a Lowe-style feature */
int d; /**< descriptor length */
double descr[FEATURE_MAX_D]; /**< descriptor */
int type; /**< feature type, OXFD or LOWE */
int category; /**< all-purpose feature category */
struct feature* fwd_match; /**< matching feature from forward image */
struct feature* bck_match; /**< matching feature from backmward image */
struct feature* mdl_match; /**< matching feature from model */
CvPoint2D64f img_pt; /**< location in image */
CvPoint2D64f mdl_pt; /**< location in model */
void* feature_data; /**< user-definable data */
};
/** holds feature data relevant to detection */
struct detection_data
{
int r;
int c;
int octv;
int intvl;
double subintvl;
double scl_octv;
};
/** default number of sampled intervals per octave */ #define SIFT_INTVLS 3 /** default sigma for initial gaussian smoothing */ #define SIFT_SIGMA 1.6 /** default threshold on keypoint contrast |D(x)| */ #define SIFT_CONTR_THR 0.04 /** default threshold on keypoint ratio of principle curvatures */ #define SIFT_CURV_THR 10 /** double image size before pyramid construction? */ #define SIFT_IMG_DBL 1 /** default width of descriptor histogram array */ #define SIFT_DESCR_WIDTH 4 /** default number of bins per histogram in descriptor array */ #define SIFT_DESCR_HIST_BINS 8 /* assumed gaussian blur for input image */ #define SIFT_INIT_SIGMA 0.5 /* width of border in which to ignore keypoints */ #define SIFT_IMG_BORDER 5 /* maximum steps of keypoint interpolation before failure */ #define SIFT_MAX_INTERP_STEPS 5 /* default number of bins in histogram for orientation assignment */ #define SIFT_ORI_HIST_BINS 36 /* determines gaussian sigma for orientation assignment */ #define SIFT_ORI_SIG_FCTR 1.5 /* determines the radius of the region used in orientation assignment */ #define SIFT_ORI_RADIUS 3.0 * SIFT_ORI_SIG_FCTR /* number of passes of orientation histogram smoothing */ #define SIFT_ORI_SMOOTH_PASSES 2 /* orientation magnitude relative to max that results in new feature */ #define SIFT_ORI_PEAK_RATIO 0.8 /* determines the size of a single descriptor orientation histogram */ #define SIFT_DESCR_SCL_FCTR 3.0 /* threshold on magnitude of elements of descriptor vector */ #define SIFT_DESCR_MAG_THR 0.2 /* factor used to convert floating-point descriptor to unsigned char */ #define SIFT_INT_DESCR_FCTR 512.0 /* returns a feature's detection data */ #define feat_detection_data(f) ( (struct detection_data*)(f->feature_data) )
输入参数：
img为输入图像；
feat为所要提取的特征指针；
intvl指的是高斯金字塔和差分金字塔的层数；
sigma指的是图像初始化过程中高斯模糊所使用的参数；
contr_thr是归一化之后的去除不稳定特征的阈值；
curv_thr指的是去除边缘的特征的主曲率阈值；
img_dbl是是否将图像放大为之前的两倍；
descr_with用来计算特征描述子的方向直方图的宽度；
descr_hist_bins是直方图中的条数
int _sift_features( IplImage* img, struct feature** feat, int intvls,
double sigma, double contr_thr, int curv_thr,
int img_dbl, int descr_width, int descr_hist_bins )
{
IplImage* init_img;
IplImage*** gauss_pyr, *** dog_pyr;
CvMemStorage* storage;
CvSeq* features;
int octvs, i, n = 0;
/* check arguments */
if( ! img )
fatal_error( "NULL pointer error, %s, line %d", __FILE__,__LINE__ );
if( ! feat )
fatal_error( "NULL pointer error, %s, line %d", __FILE__,__LINE__ );
/* 算法第一步，初始化图像 */
init_img = create_init_img( img, img_dbl, sigma );
/* 算法第二步，建立高斯差分金字塔（也就是所谓的尺度空间）最顶层4pixels
*/
octvs = log( MIN( init_img->width, init_img->height ) ) / log(2) -2; //octvs是整个金字塔层数
gauss_pyr = build_gauss_pyr( init_img, octvs, intvls, sigma ); //建立高斯金字塔
dog_pyr = build_dog_pyr( gauss_pyr, octvs, intvls ); //建立高斯差分金字塔，octvs是金字塔层数，intvls是层数（每层金字塔有几张图片）
storage = cvCreateMemStorage( 0 );
/* 算法第三步，寻找尺度空间极值，contr_thr是去除对比度低的点所采用的阀值，curv_thr是去除边缘特征所采取的阀值 */
features = scale_space_extrema( dog_pyr, octvs, intvls, contr_thr,
curv_thr, storage );
/* 算法第四步，计算特征向量的尺度 */
calc_feature_scales( features, sigma, intvls );
/* 算法第五步，调整图像的大小 */
if( img_dbl )
adjust_for_img_dbl( features );
/* 算法第六步，计算特征点的主要方向 */
calc_feature_oris( features, gauss_pyr );
/* 算法第七步，计算描述子，其中包括计算二维方向直方图并转换直方图为特征描述子 */
compute_descriptors( features, gauss_pyr, descr_width, descr_hist_bins );
/* 算法第八步，按尺度大小对描述子进行排序 */
cvSeqSort( features, (CvCmpFunc)feature_cmp, NULL );
n = features->total;
*feat = calloc( n, sizeof(struct feature) );
*feat = cvCvtSeqToArray( features, *feat, CV_WHOLE_SEQ );
for( i = 0; i < n; i++ )
{
free( (*feat)[i].feature_data );
(*feat)[i].feature_data = NULL;
}
cvReleaseMemStorage( &storage );
cvReleaseImage( &init_img );
release_pyr( &gauss_pyr, octvs, intvls + 3 );
release_pyr( &dog_pyr, octvs, intvls + 2 );
return n;
}
static IplImage* create_init_img( IplImage* img,int img_dbl,double sigma )
{
IplImage* gray, * dbl;
double sig_diff;
gray = convert_to_gray32( img );
if( img_dbl )
{
sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA * 4 );
dbl = cvCreateImage( cvSize( img->width*2, img->height*2 ),
IPL_DEPTH_32F, 1 );
cvResize( gray, dbl, CV_INTER_CUBIC );
cvSmooth( dbl, dbl, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff );
cvReleaseImage( &gray );
return dbl;
}
else
{
sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA );
cvSmooth( gray, gray, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff );
return gray;
}
}
关于图像金字塔和尺度空间的讨论，我在下面两篇文章中有涉及
这里，我再好好整理一下。
也就是说：对一张图像用不同的sigma进行高斯模糊，再相减就得到了高斯差分.
因此，建立尺度空间的简述过程如下：先建立高斯金字塔，过程如下：首先建立第1层，对原图分别用不同的sigma进行高斯模糊。其中sigma按如下规则获取：
k = pow( 2.0, 1.0 / intvls );
sig[0] = sigma;
sig[1] = sigma * sqrt( k*k- 1 );
for (i = 2; i < intvls +3; i++) // intvls是每层的照片数！ 为什么＋3等下介绍
sig[i] = sig[i-1] * k;
直观上理解，左边有2层金字塔，每层有5张图片为了在每一组中检测S个尺度的极值点，则DOG金字塔每组需S+2层图像，这是因为一个点不仅要跟周围8个点比较，同时也要跟前一张后一张的各9各点比较。而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需S+3层图像。如下：
下面用组来表示高斯金字塔层数，用层数来表示每一组的图片个数，也就是s
按照刚才的描述，我们首先建立高斯金字塔
输入参数：
octvs是高斯金字塔的组
invls是高斯金字塔的层数
sigma是初始的高斯模糊参数，后续也通过它计算每一层所使用的sigma
static IplImage*** build_gauss_pyr( IplImage* base,int octvs,
int intvls, double sigma )
{
IplImage*** gauss_pyr;
const int _intvls = intvls;
double sig[_intvls+3], sig_total, k; //+3的原因在之前已经讨论过
int i, o;
gauss_pyr = calloc( octvs, sizeof( IplImage** ) );
for( i = 0; i < octvs; i++ )
gauss_pyr[i] = calloc( intvls + 3, sizeof( IplImage *) );
k = pow( 2.0, 1.0 / intvls );
sig[0] = sigma;
sig[1] = sigma * sqrt( k*k- 1 );
for (i = 2; i < intvls +3; i++)
sig[i] = sig[i-1] * k;
for( o = 0; o < octvs; o++ )
for( i = 0; i < intvls +3; i++ )
{
if( o == 0 && i ==0 )
gauss_pyr[o][i] = cvCloneImage(base);
/* base of new octvave is halved image from end of previous octave */
else if( i ==0 )
gauss_pyr[o][i] = downsample( gauss_pyr[o-1][intvls] );
/* blur the current octave‘s last image to create the next one */
else
{
gauss_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i-1]),
IPL_DEPTH_32F, 1 );
cvSmooth( gauss_pyr[o][i-1], gauss_pyr[o][i],
CV_GAUSSIAN, 0, 0, sig[i], sig[i] );
}
}
return gauss_pyr;
}
static IplImage*** build_dog_pyr( IplImage*** gauss_pyr,int octvs,int intvls )
{
IplImage*** dog_pyr;
int i, o;
dog_pyr = calloc( octvs, sizeof( IplImage** ) );
for( i = 0; i < octvs; i++ )
dog_pyr[i] = calloc( intvls + 2, sizeof(IplImage*) );
for( o = 0; o < octvs; o++ )
for( i = 0; i < intvls +2; i++ )
{
dog_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i]),
IPL_DEPTH_32F, 1 );
cvSub( gauss_pyr[o][i+1], gauss_pyr[o][i], dog_pyr[o][i],NULL );
}
return dog_pyr;
}
根据左图的算法，与周围26个点比较，可以获得我们的候选特征点,但是获得的极值点是离散空间的极值点。还需要通过拟合三维二次函数来精确确定关键点的位置和尺度，同时要去除低对比度的关键点和不稳定的边缘响应点，增强关键点的稳定性。输入参数：
contr_thr是去除对比度低的点所采用的阈值
curv_thr是去除边缘特征的阈值
static CvSeq* scale_space_extrema( IplImage*** dog_pyr,int octvs,int intvls,
double contr_thr, int curv_thr,
CvMemStorage* storage )
{
CvSeq* features;
double prelim_contr_thr = 0.5 * contr_thr / intvls;
struct feature* feat;
struct detection_data* ddata;
int o, i, r, c;
features = cvCreateSeq( 0, sizeof(CvSeq), sizeof(struct feature), storage );
for( o = 0; o < octvs; o++ )
for( i = 1; i <= intvls; i++ ) /从一开始是因为第一层和最后一层无法产生尺度空间极大值，要跟26个点比较才行
for(r = SIFT_IMG_BORDER; r < dog_pyr[o][0]->height-SIFT_IMG_BORDER; r++)
for(c = SIFT_IMG_BORDER; c < dog_pyr[o][0]->width-SIFT_IMG_BORDER; c++)
/* 预判断对比度，如果这都过不了，该点对比度实在是非常低没必要再往下进行直接舍去 */
if( ABS( pixval32f( dog_pyr[o][i], r, c ) ) > prelim_contr_thr )
if( is_extremum( dog_pyr, o, i, r, c ) )
{
feat = interp_extremum(dog_pyr, o, i, r, c, intvls, contr_thr);
if( feat )
{
ddata = feat_detection_data( feat );
if( ! is_too_edge_like( dog_pyr[ddata->octv][ddata->intvl],
ddata->r, ddata->c, curv_thr ) )
{
cvSeqPush( features, feat );
}
else
free( ddata );
free( feat );
}
}
return features;
}
通过和对比度阈值比较去掉低对比度的点；
而通过is_extremum来判断是否为极值点，如果是则通过极值点插值的方式获取亚像素的极值点的位置。
然后通过is_too_eage_like和所给的主曲率阈值判断是否为边缘点
static int is_extremum( IplImage*** dog_pyr,int octv,int intvl,int r,int c )
{
double val = pixval32f( dog_pyr[octv][intvl], r, c );
int i, j, k;
/* check for maximum */
if( val > 0 )
{
for( i = -1; i <=1; i++ )
for( j = -1; j <=1; j++ )
for( k = -1; k <=1; k++ )
if( val < pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
return 0;
}
/* check for minimum */
else
{
for( i = -1; i <=1; i++ )
for( j = -1; j <=1; j++ )
for( k = -1; k <=1; k++ )
if( val > pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
return 0;
}
return 1;
}
D是 DOG函数，D和其偏微分在取样点计算得到
极值点x由上式得到
将（2）代入（1），可以得到：
x = (x, y, σ)T
是相对于插值中心的偏移，当它在任一维度上的偏移量大于0.5时（即x或y或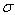
），意味着插值中心已经偏移到它的邻近点上，所以必须改变当前关键点的位置。同时在新的位置上反复插值直到收敛；也有可能超出所设定的迭代次数或者超出图像边界的范围，此时这样的点应该删除，在Lowe中进行了5次迭代。另外，
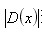过小的点易受噪声的干扰而变得不稳定，所以将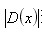小于某个经验值(Lowe论文中使用0.03，Rob Hess等人实现时使用0.04/S)的极值点删除。
获取亚像素的极值点位置
static struct feature* interp_extremum( IplImage*** dog_pyr,int octv,
int intvl, int r, int c, int intvls,
double contr_thr )
{
struct feature* feat;
struct detection_data* ddata;
double xi, xr, xc, contr;
int i = 0;
while( i < SIFT_MAX_INTERP_STEPS ) //最多循环5次
{
interp_step( dog_pyr, octv, intvl, r, c, &xi, &xr, &xc ); //实际获取亚像素位置所用到的函数
if( ABS( xi ) < 0.5 && ABS( xr ) < 0.5 && ABS( xc ) <0.5 ) //偏移小于0.5 没关系
break;
c += cvRound( xc );
r += cvRound( xr );
intvl += cvRound( xi );
if( intvl < 1 ||
intvl > intvls ||
c < SIFT_IMG_BORDER ||
r < SIFT_IMG_BORDER ||
c >= dog_pyr[octv][0]->width - SIFT_IMG_BORDER ||
r >= dog_pyr[octv][0]->height - SIFT_IMG_BORDER )
{
return NULL;
}
i++;
}
/* ensure convergence of interpolation */
if( i >= SIFT_MAX_INTERP_STEPS )
return NULL;
//去除低对比度的点，获取对比度
contr = interp_contr( dog_pyr, octv, intvl, r, c, xi, xr, xc );
if( ABS( contr ) < contr_thr / intvls )
return NULL;
feat = new_feature();
ddata = feat_detection_data( feat );
feat->img_pt.x = feat->x = ( c + xc ) * pow( 2.0, octv );
feat->img_pt.y = feat->y = ( r + xr ) * pow( 2.0, octv );
ddata->r = r;
ddata->c = c;
ddata->octv = octv;
ddata->intvl = intvl;
ddata->subintvl = xi;
return feat;
}
static void interp_step( IplImage*** dog_pyr,int octv,int intvl,int r,int c,
double* xi, double* xr, double* xc )
{
CvMat* dD, * H, * H_inv, X;
double x[3] = {0 };
//计算三维偏导数
dD = deriv_3D( dog_pyr, octv, intvl, r, c );
//计算三维海森矩阵
H = hessian_3D( dog_pyr, octv, intvl, r, c );
H_inv = cvCreateMat( 3, 3, CV_64FC1 );
cvInvert( H, H_inv, CV_SVD );
cvInitMatHeader( &X, 3, 1, CV_64FC1, x, CV_AUTOSTEP );
cvGEMM( H_inv, dD, -1, NULL, 0, &X, 0 );
cvReleaseMat( &dD );
cvReleaseMat( &H );
cvReleaseMat( &H_inv );
*xi = x[2];
*xr = x[1];
*xc = x[0];
}
static CvMat* deriv_3D( IplImage*** dog_pyr, int octv, int intvl, int r, int c )
{
CvMat* dI;
double dx, dy, ds;
dx = ( pixval32f( dog_pyr[octv][intvl], r, c+1 ) -
pixval32f( dog_pyr[octv][intvl], r, c-1 ) ) /2.0;
dy = ( pixval32f( dog_pyr[octv][intvl], r+1, c ) -
pixval32f( dog_pyr[octv][intvl], r-1, c ) ) /2.0;
ds = ( pixval32f( dog_pyr[octv][intvl+1], r, c ) -
pixval32f( dog_pyr[octv][intvl-1], r, c ) ) /2.0;
dI = cvCreateMat( 3, 1, CV_64FC1 );
cvmSet( dI, 0, 0, dx );
cvmSet( dI, 1, 0, dy );
cvmSet( dI, 2, 0, ds );
return dI;
}
/ Ixx Ixy Ixs \ <BR>
| Ixy Iyy Iys | <BR>
\ Ixs Iys Iss /
static CvMat* hessian_3D( IplImage*** dog_pyr,int octv,int intvl,int r,
int c )
{
CvMat* H;
double v, dxx, dyy, dss, dxy, dxs, dys;
v = pixval32f( dog_pyr[octv][intvl], r, c );
dxx = ( pixval32f( dog_pyr[octv][intvl], r, c+1 ) +
pixval32f( dog_pyr[octv][intvl], r, c-1 ) -2 * v );
dyy = ( pixval32f( dog_pyr[octv][intvl], r+1, c ) +
pixval32f( dog_pyr[octv][intvl], r-1, c ) -2 * v );
dss = ( pixval32f( dog_pyr[octv][intvl+1], r, c ) +
pixval32f( dog_pyr[octv][intvl-1], r, c ) -2 * v );
dxy = ( pixval32f( dog_pyr[octv][intvl], r+1, c+1 ) -
pixval32f( dog_pyr[octv][intvl], r+1, c-1 ) -
pixval32f( dog_pyr[octv][intvl], r-1, c+1 ) +
pixval32f( dog_pyr[octv][intvl], r-1, c-1 ) ) /4.0;
dxs = ( pixval32f( dog_pyr[octv][intvl+1], r, c+1 ) -
pixval32f( dog_pyr[octv][intvl+1], r, c-1 ) -
pixval32f( dog_pyr[octv][intvl-1], r, c+1 ) +
pixval32f( dog_pyr[octv][intvl-1], r, c-1 ) ) /4.0;
dys = ( pixval32f( dog_pyr[octv][intvl+1], r+1, c ) -
pixval32f( dog_pyr[octv][intvl+1], r-1, c ) -
pixval32f( dog_pyr[octv][intvl-1], r+1, c ) +
pixval32f( dog_pyr[octv][intvl-1], r-1, c ) ) /4.0;
H = cvCreateMat( 3, 3, CV_64FC1 );
cvmSet( H, 0, 0, dxx );
cvmSet( H, 0, 1, dxy );
cvmSet( H, 0, 2, dxs );
cvmSet( H, 1, 0, dxy );
cvmSet( H, 1, 1, dyy );
cvmSet( H, 1, 2, dys );
cvmSet( H, 2, 0, dxs );
cvmSet( H, 2, 1, dys );
cvmSet( H, 2, 2, dss );
return H;
}
static double interp_contr( IplImage*** dog_pyr,int octv,int intvl,int r,
int c, double xi, double xr, double xc )
{
CvMat* dD, X, T;
double t[1], x[3] = { xc, xr, xi };
cvInitMatHeader( &X, 3, 1, CV_64FC1, x, CV_AUTOSTEP );
cvInitMatHeader( &T, 1, 1, CV_64FC1, t, CV_AUTOSTEP );
dD = deriv_3D( dog_pyr, octv, intvl, r, c );
cvGEMM( dD, &X, 1, NULL, 0, &T, CV_GEMM_A_T );
cvReleaseMat( &dD );
return pixval32f( dog_pyr[octv][intvl], r, c ) + t[0] *0.5; //根据式(3)进行计算
}
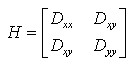
Tr(H) =Dxx+Dyy=α+β,
Det(H) =DxxDyy?(Dxy)2=αβ.
我们令 α 为H大的特征值,β是小的特征值，
令α =rβ
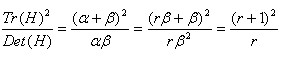
当r = 1,即α＝ β，意味着整个值最小，随着r增加，α 》 β
为了去除边缘点，只要令
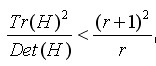，论文中采用的r =
10
static int is_too_edge_like( IplImage* dog_img,int r,int c,int curv_thr )
{
double d, dxx, dyy, dxy, tr, det;
/* principal curvatures are computed using the trace and det of Hessian */
d = pixval32f(dog_img, r, c);
dxx = pixval32f( dog_img, r, c+1 ) + pixval32f( dog_img, r, c-1 ) -2 * d;
dyy = pixval32f( dog_img, r+1, c ) + pixval32f( dog_img, r-1, c ) -2 * d;
dxy = ( pixval32f(dog_img, r+1, c+1) - pixval32f(dog_img, r+1, c-1) -
pixval32f(dog_img, r-1, c+1) + pixval32f(dog_img, r-1, c-1) ) /4.0;
tr = dxx + dyy;
det = dxx * dyy - dxy * dxy;
/* negative determinant -> curvatures have different signs; reject feature */
if( det <= 0 )
return 1;
if( tr * tr / det < ( curv_thr + 1.0 )*( curv_thr + 1.0 ) / curv_thr )
return 0;
return 1;
}
static void calc_feature_scales( CvSeq* features,double sigma,int intvls )
{
struct feature* feat;
struct detection_data* ddata;
double intvl;
int i, n;
n = features->total;
for( i = 0; i < n; i++ )
{
feat = CV_GET_SEQ_ELEM( struct feature, features, i );
ddata = feat_detection_data( feat );
intvl = ddata->intvl + ddata->subintvl;
feat->scl = sigma * pow( 2.0, ddata->octv + intvl / intvls );
ddata->scl_octv = sigma * pow( 2.0, intvl / intvls );
}
}
static void adjust_for_img_dbl( CvSeq* features )
{
struct feature* feat;
int i, n;
n = features->total;
for( i = 0; i < n; i++ )
{
feat = CV_GET_SEQ_ELEM( struct feature, features, i );
feat->x /= 2.0;
feat->y /= 2.0;
feat->scl /= 2.0;
feat->img_pt.x /= 2.0;
feat->img_pt.y /= 2.0;
}
}
为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个主方向。对于在DOG金字塔中检测出的关键点，采集其所在高斯金字塔图像3σ领域窗口内像素的梯度和方向分布特征。
给每一个图像特征向量计算规范化的方向
static void calc_feature_oris( CvSeq* features, IplImage*** gauss_pyr )
{
struct feature* feat;
struct detection_data* ddata;
double* hist;
double omax;
int i, j, n = features->total;
for( i = 0; i < n; i++ )
{
feat = malloc( sizeof( struct feature ) );
cvSeqPopFront( features, feat );
ddata = feat_detection_data( feat );
hist = ori_hist( gauss_pyr[ddata->octv][ddata->intvl],
ddata->r, ddata->c, SIFT_ORI_HIST_BINS,
cvRound( SIFT_ORI_RADIUS * ddata->scl_octv ),
SIFT_ORI_SIG_FCTR * ddata->scl_octv );
for( j = 0; j < SIFT_ORI_SMOOTH_PASSES; j++ )
smooth_ori_hist( hist, SIFT_ORI_HIST_BINS );
omax = dominant_ori( hist, SIFT_ORI_HIST_BINS );
add_good_ori_features( features, hist, SIFT_ORI_HIST_BINS,
omax * SIFT_ORI_PEAK_RATIO, feat );
free( ddata );
free( feat );
free( hist );
}
}
我们一个个来看这些函数
对所给像素计算灰度方向直方图
以关键点为中心的邻域窗口内采样，并用直方图统计邻域像素的梯度
方向。梯度直方图的范围是0～360度，其中每10度一个柱，总共36个柱
static double* ori_hist( IplImage* img,int r,int c,int n,int rad,
double sigma )
{
double* hist;
double mag, ori, w, exp_denom, PI2 = CV_PI *2.0;
int bin, i, j;
hist = calloc( n, sizeof( double ) );
exp_denom = 2.0 * sigma * sigma;
for( i = -rad; i <= rad; i++ )
for( j = -rad; j <= rad; j++ )
if( calc_grad_mag_ori( img, r + i, c + j, &mag, &ori ) )
{
w = exp( -( i*i + j*j ) / exp_denom );
bin = cvRound( n * ( ori + CV_PI ) / PI2 );
bin = ( bin < n )? bin : 0;
hist[bin] += w * mag;
}
return hist;
}
static int calc_grad_mag_ori( IplImage* img,int r,int c,double* mag,
double* ori )
{
double dx, dy;
if( r > 0 && r < img->height -1 && c >0 && c < img->width -1 )
{
dx = pixval32f( img, r, c+1 ) - pixval32f( img, r, c-1 );
dy = pixval32f( img, r-1, c ) - pixval32f( img, r+1, c );
*mag = sqrt( dx*dx + dy*dy );
*ori = atan2( dy, dx );
return 1;
}
else
return 0;
}
static void smooth_ori_hist(double* hist,int n )
{
double prev, tmp, h0 = hist[0];
int i;
prev = hist[n-1];
for( i = 0; i < n; i++ )
{
tmp = hist[i];
//采用[0.25,0.5,0.25]的模版，作高斯模糊
hist[i] = 0.25 * prev + 0.5 * hist[i] +
0.25 * ( ( i+1 == n )? h0 : hist[i+1] );
prev = tmp;
}
}
static double dominant_ori(double* hist,int n )
{
double omax;
int maxbin, i;
omax = hist[0];
maxbin = 0;
for( i = 1; i < n; i++ )
if( hist[i] > omax )
{
omax = hist[i];
maxbin = i;
}
return omax;
}
#define interp_hist_peak( l, c, r ) ( 0.5 * ((l)-(r)) / ((l) -2.0*(c) + (r)) )
static void add_good_ori_features( CvSeq* features,double* hist,int n,
double mag_thr, struct feature* feat )
{
struct feature* new_feat;
double bin, PI2 = CV_PI * 2.0;
int l, r, i;
for( i = 0; i < n; i++ )
{
l = ( i == 0 )? n - 1 : i-1;
r = ( i + 1 ) % n;
if( hist[i] > hist[l] && hist[i] > hist[r] && hist[i] >= mag_thr )
{
bin = i + interp_hist_peak( hist[l], hist[i], hist[r] );
bin = ( bin < 0 )? n + bin : ( bin >= n )? bin - n : bin;
new_feat = clone_feature( feat );
new_feat->ori = ( ( PI2 * bin ) / n ) - CV_PI;
cvSeqPush( features, new_feat );
free( new_feat );
}
}
}
每个关键点包含位置，尺度和方向3个特征。
static void compute_descriptors( CvSeq* features, IplImage*** gauss_pyr,int d,
int n )
{
struct feature* feat;
struct detection_data* ddata;
double*** hist;
int i, k = features->total;
for( i = 0; i < k; i++ )
{
feat = CV_GET_SEQ_ELEM( struct feature, features, i );
ddata = feat_detection_data( feat );
hist = descr_hist( gauss_pyr[ddata->octv][ddata->intvl], ddata->r,
ddata->c, feat->ori, ddata->scl_octv, d, n );
hist_to_descr( hist, d, n, feat );
release_descr_hist( &hist, d );
}
}
static double*** descr_hist( IplImage* img,int r,int c,double ori,
double scl, int d, int n )
{
double*** hist;
double cos_t, sin_t, hist_width, exp_denom, r_rot, c_rot, grad_mag,
grad_ori, w, rbin, cbin, obin, bins_per_rad, PI2 = 2.0 * CV_PI;
int radius, i, j;
hist = calloc( d, sizeof( double** ) );
for( i = 0; i < d; i++ )
{
hist[i] = calloc( d, sizeof( double* ) );
for( j = 0; j < d; j++ )
hist[i][j] = calloc( n, sizeof( double ) );
}
cos_t = cos( ori );
sin_t = sin( ori );
bins_per_rad = n / PI2;
exp_denom = d * d * 0.5;
hist_width = SIFT_DESCR_SCL_FCTR * scl;
radius = hist_width * sqrt(2) * ( d + 1.0 ) * 0.5 + 0.5; //利用上面的半径公式，计算出区域半径
for( i = -radius; i <= radius; i++ )
for( j = -radius; j <= radius; j++ )
{
/*
Calculate sample‘s histogram array coords rotated relative to ori.
Subtract 0.5 so samples that fall e.g. in the center of row 1 (i.e.
r_rot = 1.5) have full weight placed in row 1 after interpolation.
*/
c_rot = ( j * cos_t - i * sin_t ) / hist_width; //保持旋转不变性
r_rot = ( j * sin_t + i * cos_t ) / hist_width;
rbin = r_rot + d / 2 - 0.5; //计算落在子区域的下标
cbin = c_rot + d / 2 - 0.5;
if( rbin > -1.0 && rbin < d && cbin > -1.0 && cbin < d )
if( calc_grad_mag_ori( img, r + i, c + j, &grad_mag, &grad_ori ))
{
grad_ori -= ori;
while( grad_ori < 0.0 )
grad_ori += PI2;
while( grad_ori >= PI2 )
grad_ori -= PI2;
obin = grad_ori * bins_per_rad;
//Lowe建议子区域的像素的梯度大小按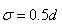
的高斯加权计算，即
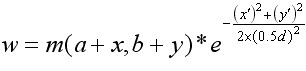
w = exp( -(c_rot * c_rot + r_rot * r_rot) / exp_denom );
interp_hist_entry( hist, rbin, cbin, obin, grad_mag * w, d, n );
}
}
return hist;
}
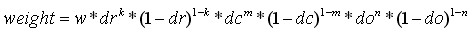
static void interp_hist_entry(double*** hist,double rbin,double cbin,
double obin, double mag, int d, int n )
{
double d_r, d_c, d_o, v_r, v_c, v_o;
double** row, * h;
int r0, c0, o0, rb, cb, ob, r, c, o;
r0 = cvFloor( rbin );
c0 = cvFloor( cbin );
o0 = cvFloor( obin );
d_r = rbin - r0;
d_c = cbin - c0;
d_o = obin - o0;
/*
The entry is distributed into up to 8 bins. Each entry into a bin
is multiplied by a weight of 1 - d for each dimension, where d is the
distance from the center value of the bin measured in bin units.
*/
for( r = 0; r <=1; r++ )
{
rb = r0 + r;
if( rb >= 0 && rb < d )
{
v_r = mag * ( ( r == 0 )? 1.0 - d_r : d_r );
row = hist[rb];
for( c = 0; c <=1; c++ )
{
cb = c0 + c;
if( cb >= 0 && cb < d )
{
v_c = v_r * ( ( c == 0 )? 1.0 - d_c : d_c );
h = row[cb];
for( o = 0; o <= 1; o++ )
{
ob = ( o0 + o ) % n;
v_o = v_c * ( ( o == 0 )? 1.0 - d_o : d_o );
h[ob] += v_o;
}
}
}
}
}
}
static void hist_to_descr(double*** hist,int d,int n,struct feature* feat )
{
int int_val, i, r, c, o, k = 0;
for( r = 0; r < d; r++ )
for( c = 0; c < d; c++ )
for( o = 0; o < n; o++ )
feat->descr[k++] = hist[r][c][o];
feat->d = k;
normalize_descr( feat );
for( i = 0; i < k; i++ )
if( feat->descr[i] > SIFT_DESCR_MAG_THR )
feat->descr[i] = SIFT_DESCR_MAG_THR;
normalize_descr( feat );
/* 描述子向量门限。非线性光照，相机饱和度变化对造成某些方向的梯度值过大，而对方向的影响微弱。因此设置门限值(向量归一化后，一般取0.2)截断较大的梯度值。然后，再进行一次归一化处理，提高特征的鉴别性。 */
for( i = 0; i < k; i++ )
{
int_val = SIFT_INT_DESCR_FCTR * feat->descr[i];
feat->descr[i] = MIN( 255, int_val );
}
}
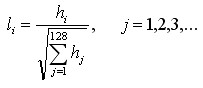
static void normalize_descr(struct feature* feat )
{
double cur, len_inv, len_sq = 0.0;
int i, d = feat->d;
for( i = 0; i < d; i++ )
{
cur = feat->descr[i];
len_sq += cur*cur;
}
len_inv = 1.0 / sqrt( len_sq );
for( i = 0; i < d; i++ )
feat->descr[i] *= len_inv;
}
算法第8步：按特征点尺度对特征点描述向量进行排序
static int feature_cmp(void* feat1,void* feat2,void* param )
{
struct feature* f1 = (struct feature*) feat1;
struct feature* f2 = (struct feature*) feat2;
if( f1->scl < f2->scl )
return 1;
if( f1->scl > f2->scl )
return -1;
return 0;
}
#include <opencv2/opencv.hpp>
#include <opencv2/nonfree/nonfree.hpp>
#include <opencv2/nonfree/features2d.hpp>
using namespace std;
using namespace cv;
int main()
{
Mat image = imread("./building.jpg");
Mat gray;
cvtColor( image, gray, CV_RGB2GRAY );
Mat descriptors;
vector<KeyPoint> keypoints;
initModule_nonfree();
Ptr<Feature2D> sift = Algorithm::create<Feature2D>("Feature2D.SIFT");
(*sift)(gray, noArray(), keypoints, descriptors);
drawKeypoints(image, keypoints, image, Scalar(255,0,0),4);
imshow("test", image);
waitKey();
}
1)SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定 程度的稳定性；
2)独特性好，信息量丰富，适用于海量特征数据库中进行快速、准确的匹配；
3)多量性，即使少数的几个物体也可以产生大量的SIFT特征向量；
4)高速性，经优化的SIFT匹配算法可以达到实时的要求；
5)可扩展性，可以很方便的与其他形式的特征向量进行联合。
2）有时特征点较少；
3）对边缘光滑的目标无法准确提取特征点。
SIFT在图像的不变特征提取方面拥有优势，但存在着实时性不高、有时特征点较少、对边缘模糊的目标无法准确提取特征点等缺陷。
PCA是一种数据降维技术。通过降维技术，可有效化简SIFT算子的128维描述子。
彩色尺度特征不变变换，可以针对彩色图像进行图像的不变特征提取。
两个向量空间之间的一个仿射变换。ASIFT可以抵抗强仿射情况，提取的特征点远多于SIFT算法。
|
|
SIFT |
SURF |
|
特征点检测 |
用不同尺度的高斯函数与图像做卷积 |
用不同大小的box filter与原始图像做卷积，易于并行 |
|
方向 |
特征点邻域内，利用梯度直方图计算 |
特征点邻接圆域内，计算x、y方向上的Haar小波响应 |
|
描述符生成 |
20*20(单位为pixel)区域划分为4*4(或2*2)的子区域，每个子域计算8bin直方图 |
20*20(单位为sigma)区域划分为4*4子域，每个子域计算5*5个采样点的Haar小波响 应，记录∑dx, ∑dy, ∑|dx|,∑|dy|。 |
OpenCV2马拉松第27圈——SIFT论文，原理及源码解读,布布扣,bubuko.com
OpenCV2马拉松第27圈——SIFT论文，原理及源码解读
原文地址：http://blog.csdn.net/abcd1992719g/article/details/28913101
