算法导论读书笔记(17)
动态规划概述
和分治法一样, 动态规划 (dynamic programming)是通过组合子问题的解而解决整个问题的。分治法是将问题划分成一些独立的子问题,递归地求解各子问题,然后合并子问题的解而得到原问题的解。与此不同,动态规划适用于子问题并不独立的情况,即各子问题包含公共的子子问题。在这种情况下,分治法会重复地求解公共的子子问题。而动态规划算法对每个子问题只求解一次,将其结果保存在一张表中,从而避免重复。
动态规划通常用于 最优化问题 。此类问题可能有多种可行解。每个解有一个值,而我们希望找出具有最优(最大或最小)值的解。称这样的解为该问题的“一个”最优解(而不是“确定的”最优解),因而可能存在多个最优解。
动态规划算法的设计可以分为如下4个步骤:
- 描述最优解的结构
- 递归定义最优解的值
- 按自底向上的方式计算最优解的值
- 由计算出的结构构造一个最优解
钢条切割
钢条切割问题是动态规划问题的一个例子。塞林企业会买进长钢条,将它们切割成短条后卖出(切割是免费的,不计成本)。塞林企业的老总想要知道钢条怎么切割最赚钱。
已知塞林企业对长度为 i 英寸的钢条的售价为 pi 美元,其中 i = 1,2,…。下图给出了一张样本价格表。
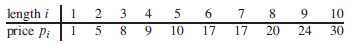
钢条切割问题 的描述如下。给定一根长为 n 的钢条以及价格表 pi ,其中 i = 1,2,…, n ,找出钢条切割并卖出后可取得的最大收益 rn 。
考虑一下 n = 4的情况。下图列出了切割4英寸钢条的所有方式。根据样本价格表,最后可知将4英寸钢条切割成2根2英寸钢条的收益最大。 p2 + p2 = 10。
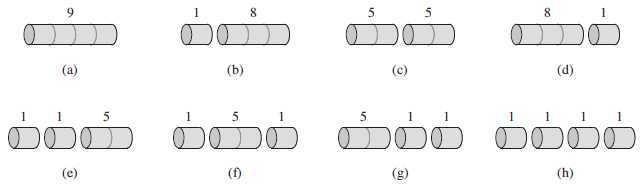
一根长度为 n 的钢条共有 2n-1 种不同的切割方式。我们这里用普通加法符号表示一个分解,比如7 = 2 + 2 + 3就表示一根长度为7的钢条被切成3份,2根长度为2,一根长度为3。如果最优解将钢条切割成 k 份( 1 <= k <= n ),那么最优分解即为 n = i1 + i2 + … + ik ,每段钢条的长度为 i1 , i2 ,…, ik ,对应的最大收益为 rn = pi1 + pi2 + … + pik 。
一般来说,我们可以将最优收益 rn 表示成如下形式:
rn = max (
pn , r1 +
rn-1 , r2 +
rn-2 ,…, rn-1 +
r1 )
第一个参数 pn 代表不切割时钢条的价格。其它的 n - 1个参数首先将钢条分为2份,长度分别为 i 和 n - i ( i = 1,2,…, n - 1),然后分别取得两份的最优收益 ri 和 rn-i 之后做和。因为我们不知道 i 取值为多少时会得到最优解,所以我们必须计算所有可能情况并从中选出最优解。
可以看到,为了解决规模为 n 的初始问题,我们首先要解决的是规模小一些的同类型问题。一旦我们做出了一个划分,我们就可以将划分出的两部分视为钢条切割问题的独立的实例。整体最优解就包含在这相关的两部分子问题之中。我们说钢条切割问题满足 最优子结构 的性质:某问题的最优解由相关子问题的最优解组合而成,且这些子问题可以独立求解。
下面以一种简单的方式安排钢条切割的递归结构,我们能看到一个分解是由位于左侧长度为 i 的一份,以及位于右侧的剩余部分 n - i 。只有右侧的部分可能再次被分解。这样可以得到一个更简洁的公式:
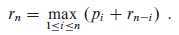
在上面的公式中,最优解只和一个相关的子问题有关(划分后右侧的剩余部分)。
自顶向下的递归实现
下面的过程是一种很直接的,自顶向下,递归风格的实现。
CUT-ROD(p, n) 1 if n == 0 2 return 0 3 q = -∞ 4 for i = 1 to n 5 q = max(q, p[i] + CUT-ROD(p, n - i)) 6 return q
过程 CUT-ROD 接受一个价格的数组 p [ 1 .. n ]和一个整数
n 作为参数,返回可能的最优解。如果你用自己最熟悉的语言实现了这个 CUT-ROD
过程并运行它,你会发现即使对于不太大的 n 值,你的程序也会花很长的时间才能得出结果。实际上,每次你将 n
值增加1,你的程序的运行时间大约要翻一番。
过程 CUT-ROD 的效率如此低下的原因就是它不断的重复解决相同的子问题。下图给出了一个很好的说明,其中 n
= 4,可以看到,过程多次重复计算 n = 2和 n = 1。
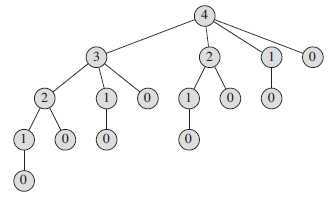
为了分析 CUT-ROD 的运行时间,设 T ( n )为问题规模为 n
时调用 CUT-ROD 的总次数,该表达式等于根结点标记为 n
的递归树中的总结点数。该总数包含根结点上的初始调用。因此, T ( 0 ) = 1和
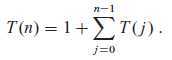
其中 j = n - i ,可得 T ( n ) =
2n ,因此 CUT-ROD 的运行时间是 n 的幂。
使用动态规划解决钢条切割问题
可以看到,递归算法之所以效率低下,是因为它反复求解相同的子问题。,因此,动态规划会仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来以便之后查找。由此可见,动态规划需要额外的内存空间来节省计算时间,是典型的 时空权衡 (time-memory trade-off)的例子。
动态规划有两种等价的实现方法。
- 带备忘的自顶向下法(top-down with memoization)
- 此方法仍按自然的递归形式编写过程,但过程会保存每个子问题的解。
- 自底向上法(bottom-up method)
- 这种方法一般需要恰当定义子问题“规模”的概念,使得任何子问题的求解都只依赖于“更小”子问题的求解。因而我们可以将子问题按规模排序,由小到大一次求解。当求解某子问题时,它所依赖的那些更小子问题都已求解完毕,因此每个子问题只求解一次。
两种方法得到的算法具有相同的渐进运行时间,但自底向上方法的时间函数通常具有更小的系数。
下面给出的是自顶向下 CUT-ROD 过程的伪码,加入了备忘机制:
MEMOIZED-CUT-ROD(p, n) 1 let r[0..n] be a new array 2 for i = 0 to n 3 r[i] = -∞ 4 return MEMOIZED-CUT-ROD-AUX(p, n, r)
MEMOIZED-CUT-ROD-AUX(p, n, r) 1 if r[n] >= 0 2 reutrn r[n] 3 if n == 0 4 q = 0 5 else 6 q = -∞ 7 for i = 1 to n 8 q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n - i, r)) 9 r[n] = q 10 return q
过程 MEMOIZED-CUT-ROD 首先检查值是否已知,如果是,则返回;否则在第6~8行计算值 q
,第9行将 q 存入 r [ n ],最后返回 q 。
自底向上版本更简单:
BOTTOM-UP-CUT-ROD(p, n) 1 let r[0..n] be a new array 2 r[0] = 0 3 for j = 1 to n 4 q = -∞ 5 for i = 1 to j 6 q = max(q, p[i] + r[j - i]) 7 r[j] = q 8 return r[n]
过程 BOTTOM-UP-CUT-ROD 采用子问题的自然顺序:若 i < j
,则规模为 i 的子问题比规模为 j 的子问题“更小”。因此,过程依次求解规模为 j = 0,1,…,
n 的子问题。
子问题图
当思考一个动态规划为问题时,我们应该了解问题的子问题之间的依赖关系。
问题的 子问题图 准确地表达了这些信息,子问题图是一个有向图,每个定点唯一地对应一个子问题。如果求子问题 x 的最优解时需要直接用到子问题 y 的最优解,那么在子问题图中就会有一条从子问题 x 到子问题 y 的有向边。下图显示了 n = 4时钢条切割问题的子问题图。
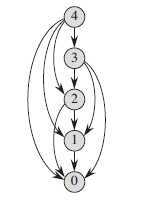
子问题图 G = ( V , E )的规模可以帮助我们确定动态规划的运行时间。由于每个子问题只求解一次,因此算法运行时间等于每个子问题求解时间之和。通常,一个子问题的求解时间与子问题图中对应顶点的度成正比,而子问题的数目等于子问题的顶点数。因此,通常情况下,动态规划算法的运行时间与顶点和边的数量呈线性关系。
重构解
上面的算法仅返回最优解的收益值,并未返回解本身。这里可以扩展该算法。
EXTENDED-BOTTOM-UP-CUT-ROD(p, n) 1 let r[0..n] and s[0..n] be new arrays 2 r[0] = 0 3 for j = 1 to n 4 q = -∞ 5 for i = 1 to j 6 if q < p[i] + r[j - i] 7 q = p[i] + r[j - i] 8 s[j] = i 9 r[j] = q 10 return r and s
钢条切割问题的简单Java实现
/** * 带备忘的自顶向下方法 * * @param price 价格表 * @param n 待分割的长度 */ public static int memoizedCutRod(int[] price, int n) { int[] revenue = new int[n + 1]; for (int i = 0; i < revenue.length; i++) // 初始化revenue数组 revenue[i] = Integer.MIN_VALUE; return memoizedCutRodAux(price, n, revenue); } private static int memoizedCutRodAux(int[] price, int n, int[] revenue) { int q; if (revenue[n] >= 0) // 如果revenue数组中有记录,就返回数组中的结果 return revenue[n]; if (n == 0) q = 0; else { q = Integer.MIN_VALUE; for (int i = 1; i <= n; i++) q = Integer.max(q, price[i] + memoizedCutRodAux(price, n - i, revenue)); revenue[n] = q; } return q; } /** * 自底向上法 * * @param price 价格表 * @param n 待分割的长度 */ public static int bottomUpCutRod(int[] price, int n) { int[] revenue = new int[n + 1]; int q; revenue[0] = 0; for (int j = 1; j <= n; j++) { q = Integer.MIN_VALUE; for (int i = 1; i <= j; i++) q = Integer.max(q, price[i] + revenue[j - i]); revenue[j] = q; } return revenue[n]; }
