最大全0/1子矩阵的探究

标签：

最大全0/1子矩阵的探究

by MedalPluS

  【问题模型】

    给定一个n*n的矩阵，求矩阵中面积最大的一个值全是0或1的子矩阵

  【分析】

    （这里n*n完全可以改为n*m，但由于种种原因，等下代码里是n*n）

    首先很容易想到一种解法，枚举这个子矩阵的左上方，和右下方，然后暴力统计，这样时间复杂度O(N⁶)，这种做法很广泛

    这肯定是不能满足我们的需求，那么应该怎么办呢？我们发现O(n^₂)的时间浪费在统计上，我们可以使用前缀和的手段，预处理

    这样时间复杂度O(n⁴)，还是很垃圾

    在暴力种种优化都不行的时候，想一想贪心或者数学或者DP把！——无名氏

    贪心：这肯定是不对的

    DP：转移方程太难推出

    数学：这个我可以

          对于3*3的矩阵

          0 1 1

          1 0 0

          1 1 1

          求全1矩阵

          我们可以逐行算！

          比如说设f(i)表示第i列的已经连续的全1的子矩阵的长度

          处理第一行，可以发现f(1)=0,f(2)=1,f(3)=1

          映射到数轴上，可以发现是这样的：

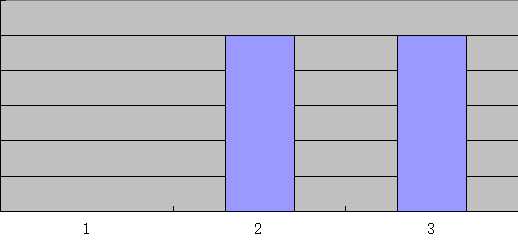
          面积最大全1矩阵很明显是1+1=2，记录下来，发现了没？其实就是直方图最大面积

          继续处理第二行，此时f(1)=1,f(2)=0,f(3)=0

          映射到数轴上，可以发现是这样的：

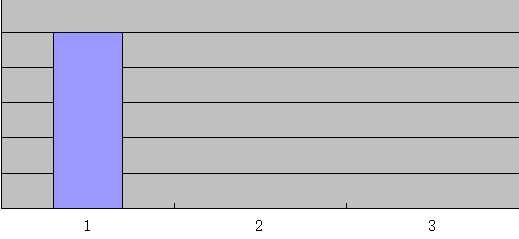
          最大面积为1，而没有原来的2小，所以不记录

          处理第三行，此时f(1)=2,f(2)=1,f(3)=1

          映射到数轴上

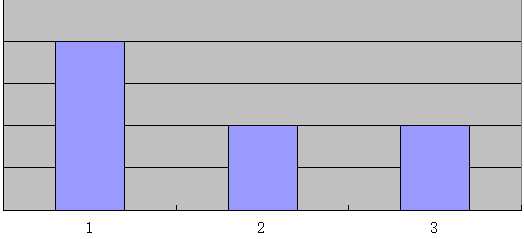
           轻易地算出最大面积为3，比2大，更换

          扫描结束，最大值为3，而正好是答案

  【实现】

      那么具体应该如何实现呢？

      同上，设f()，再设l(),r(),表示第i行以f(i)为最大值的直方图的左端点l(i)和右端点r(i)

      显然，这行的结果为f(i)*((r(i)-l(i)+1)

       每次累计最大值

      输出即可

   【代码】

 1 #include <iostream>
 2 #include <cstdio>
 3 using namespace std;
 4 
 5 const int maxn=2001;
 6 
 7 int a[maxn][maxn],n,ans;
 8 int l[maxn],r[maxn],b[maxn];
 9 
10 int main(){
11     int i,j;
12     scanf("%d",&n);
13     for(i=1;i<=n;i++){
14       for(j=1;j<=n;j++){
15         scanf("%d",&a[i][j]);
16         if(!a[i][j])b[j]++;//注意这里指的是全0子矩阵，如果是求全1子矩阵的话，应该改为if(a[i][j])b[j]++;想想为什么
17         else b[j]=0;
18       }
19       for(j=1;j<=n;j++)//求出l
20       {
21         l[j]=j;
22         while(l[j]-1>=1 && b[l[j]-1]>=b[j])
23           l[j]=l[l[j]-1];
24       }
25       for(j=n;j>=1;j--)//求出r
26       {
27         r[j]=j;
28         while(r[j]+1<=n && b[r[j]+1]>=b[j])
29           r[j]=r[r[j]+1];
30       }
31       for(j=1;j<=n;j++)//算出面积
32         if(b[j] && ans<b[j]*(r[j]-l[j]+1))
33           ans=b[j]*(r[j]-l[j]+1);
34     }
35     printf("%d",ans);
36     return 0;
37 }

最大全0/1子矩阵的探究

标签：

原文地址：http://www.cnblogs.com/maopengsen/p/4430775.html