POJ 1003

标签：java   poj   

Description

How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We‘re assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

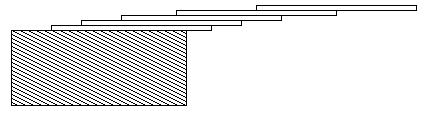
Input

Output

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

import java.math.BigDecimal;
import java.math.BigInteger;
import java.math.MathContext;
import java.util.Scanner;

public class Poj1003 {

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
			String temp = sc.next();
			if (temp.equals("0.00")) {
				break;
			}
			BigDecimal inputVal = new BigDecimal(temp);

			ok: for (int i = 1; i < 1000; i++) {
				Rational result = new Rational(BigInteger.ZERO, BigInteger.ONE);
				for (int j = 1; j <= i; j++) {
					result = result.add(new Rational(BigInteger.ONE, BigInteger.valueOf(j + 1)));
				}
				BigDecimal tempval = result.getVal();
				if (tempval.compareTo(inputVal) >= 1) {
					System.out.println(i + " card(s)");
					break ok;
				}
			}
		}

	}

}

/**
 *	定义一个有理数类
 */
class Rational {
	//设置小数点之后的精确位数
	private static MathContext mc = new MathContext(4);
	
	private BigInteger a; //表示分子
	private BigInteger b; //表示分母

	public Rational(BigInteger a, BigInteger b) {
		//求出a和b的最大公约数
		BigInteger c = a.gcd(b);
		//对分子和分母进行约分
		this.a = a.divide(c);
		this.b = b.divide(c);
	}
	
	//有理数的加法
	public Rational add(Rational x) {
		return new Rational(this.a.multiply(x.b).add(x.a.multiply(this.b)),
				this.b.multiply(x.b));
	}
	
	//返回本有理数对应的小数
	public BigDecimal getVal() {
		return new BigDecimal(this.a).divide(new BigDecimal(this.b), mc);
	}

}

POJ 1003

标签：java   poj   

原文地址：http://blog.csdn.net/bear_huangzhen/article/details/45071383