JGShining‘s kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they‘re unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don‘t wanna build a road with other poor ones, and rich ones also can‘t abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1,  Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

For each test case, output the result in the form of sample.
You should tell JGShining what‘s the maximal number of road(s) can be built.

2
1 2
2 1
3
1 2
2 3
3 1

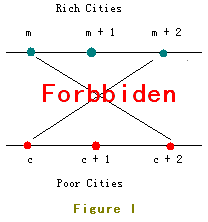
Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint
Huge input, scanf is recommended.
 

JGShining（极光炫影）

这种

最长上升子序列(LIS)长度的O(nlogn)算法的学习过程，借鉴了他人博客文章算法介绍：http://www.cnblogs.com/mengxm-lincf/archive/2011/07/12/2104745.html

在川大oj上遇到一道题无法用n^2过于是，各种纠结，最后习得nlogn的算法

最长递增子序列，Longest Increasing Subsequence 下面我们简记为 LIS。
排序+LCS算法 以及 DP算法就忽略了，这两个太容易理解了。

假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7，可以看出来它的LIS长度为5。n
下面一步一步试着找出它。
我们定义一个序列B，然后令 i = 1 to 9 逐个考察这个序列。
此外，我们用一个变量Len来记录现在最长算到多少了

首先，把d[1]有序地放到B里，令B[1] = 2，就是说当只有1一个数字2的时候，长度为1的LIS的最小末尾是2。这时Len=1

然后，把d[2]有序地放到B里，令B[1] = 1，就是说长度为1的LIS的最小末尾是1，d[1]=2已经没用了，很容易理解吧。这时Len=1

接着，d[3] = 5，d[3]>B[1]，所以令B[1+1]=B[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，很容易理解吧。这时候B[1..2] = 1, 5，Len＝2

再来，d[4] = 3，它正好加在1,5之间，放在1的位置显然不合适，因为1小于3，长度为1的LIS最小末尾应该是1，这样很容易推知，长度为2的LIS最小末尾是3，于是可以把5淘汰掉，这时候B[1..2] = 1, 3，Len = 2

继续，d[5] = 6，它在3后面，因为B[2] = 3, 而6在3后面，于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6，还是很容易理解吧？ Len = 3 了噢。

第6个, d[6] = 4，你看它在3和6之间，于是我们就可以把6替换掉，得到B[3] = 4。B[1..3] = 1, 3, 4， Len继续等于3

第7个, d[7] = 8，它很大，比4大，嗯。于是B[4] = 8。Len变成4了

第8个, d[8] = 9，得到B[5] = 9，嗯。Len继续增大，到5了。

最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，所以我们知道，最新的B[4] =7，B[1..5] = 1, 3, 4, 7, 9，Len = 5。

于是我们知道了LIS的长度为5。

!!!!! 注意。这个1,3,4,7,9不是LIS，它只是存储的对应长度LIS的最小末尾。有了这个末尾，我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义，但是如果后面再出现两个数字 8 和 9，那么就可以把8更新到d[5], 9更新到d[6]，得出LIS的长度为6。

然后应该发现一件事情了：在B中插入数据是有序的，而且是进行替换而不需要挪动——也就是说，我们可以使用二分查找，将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)～！

通俗的理解很容易，可以这样理解，用后面的元素替换dp【】中比此元素大一点儿得数，这个过程保证了len不变，即最长递增子序列不变，那么替换为较小的元素，是为了使

更后面的元素更有“机会”加入到dp【】末尾使len更增1，换句话说使序列更长的潜力增大了。

 

同时注意输出格式细节。road 和roads。同时注意那个二分查找的最后一定是low大于high且 per【low】.y大于所要查找的数

AC：

#include<iostream>
#include<stdio.h>
#include<algorithm>
const int M=500000+10;
using namespace std;
struct city
{
    int x,y;
}per[M];
bool cmp(city a,city b)
{
    return a.x<b.x;
}
int main()
{
    int n,dp[M],t=0;
    while(cin>>n)
    {
        for(int i=0;i<n;i++)
           scanf("%d%d",&per[i].x,&per[i].y);
        sort(per,per+n,cmp);
        int len=1,low,high;
        dp[1]=per[0].y;
        for(int j=1;j<n;j++)
        {
            if(per[j].y>dp[len])
                dp[++len]=per[j].y;
            else
            {
                low=1;high=len;
                    while(low<=high)
                    {
                        int mid=(low+high)/2;
                        if(per[j].y>dp[mid])
                            low=mid+1;
                        else
                            high=mid-1;
                    }
                    dp[low]=per[j].y;


            }

        }
        if(len==1)
        cout<<"Case "<<++t<<":\n"<<"My king, at most "<<len<<" road can be built."<<endl;
        else
            cout<<"Case "<<++t<<":\n"<<"My king, at most "<<len<<" roads can be built."<<endl;
        cout<<"\n";
    }
    return 0;
}