Largest Rectangle in Histogram

标签：

以下全部抄自“李二娃的博客”，地址 http://www.cnblogs.com/lichen782/p/leetcode_Largest_Rectangle_in_Histogram.html

说的超详细超有画面感，多谢作者的解释！

==========羞羞的引用转载开始==============

16行，给跪了。。。。

这个我不去debug下都特么不知道在干嘛。

那要不就debug下看看这段代码在做神马。例子就用题目中的[2,1,5,6,2,3]吧。

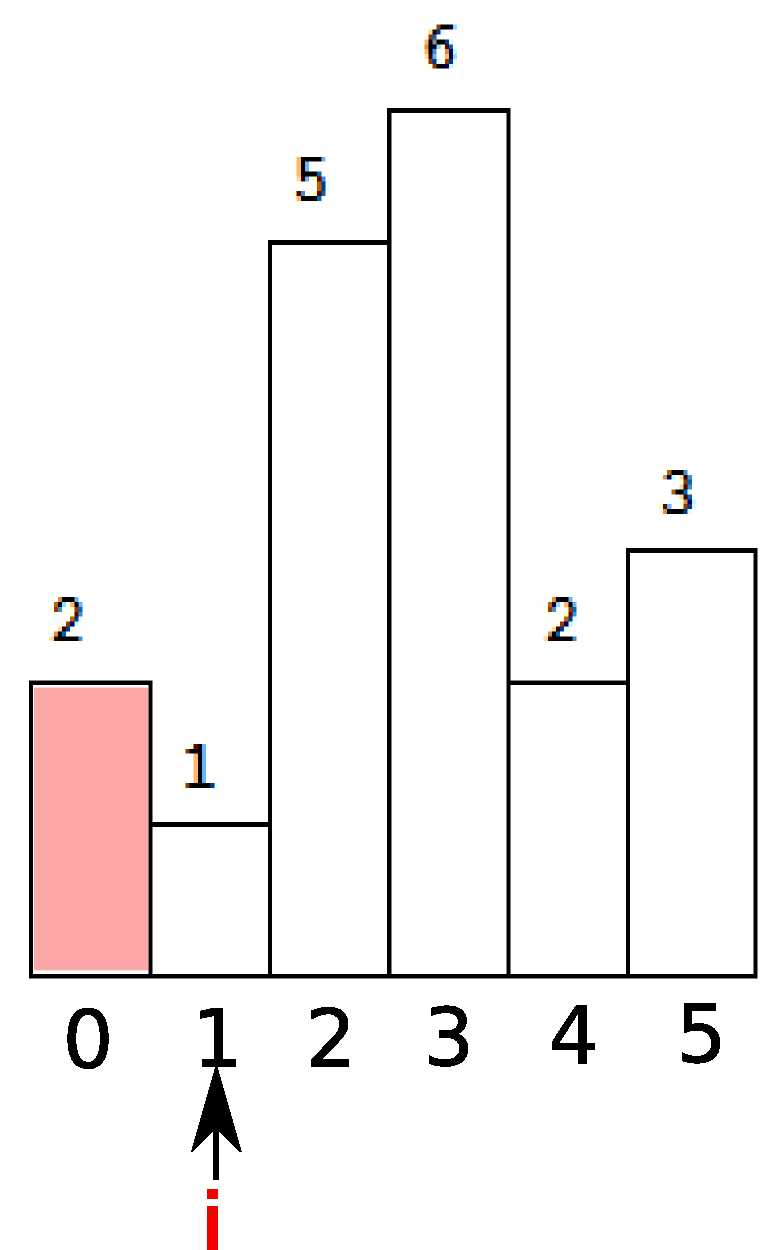
首先，如果栈是空的，那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引，不是高度。然后i++。

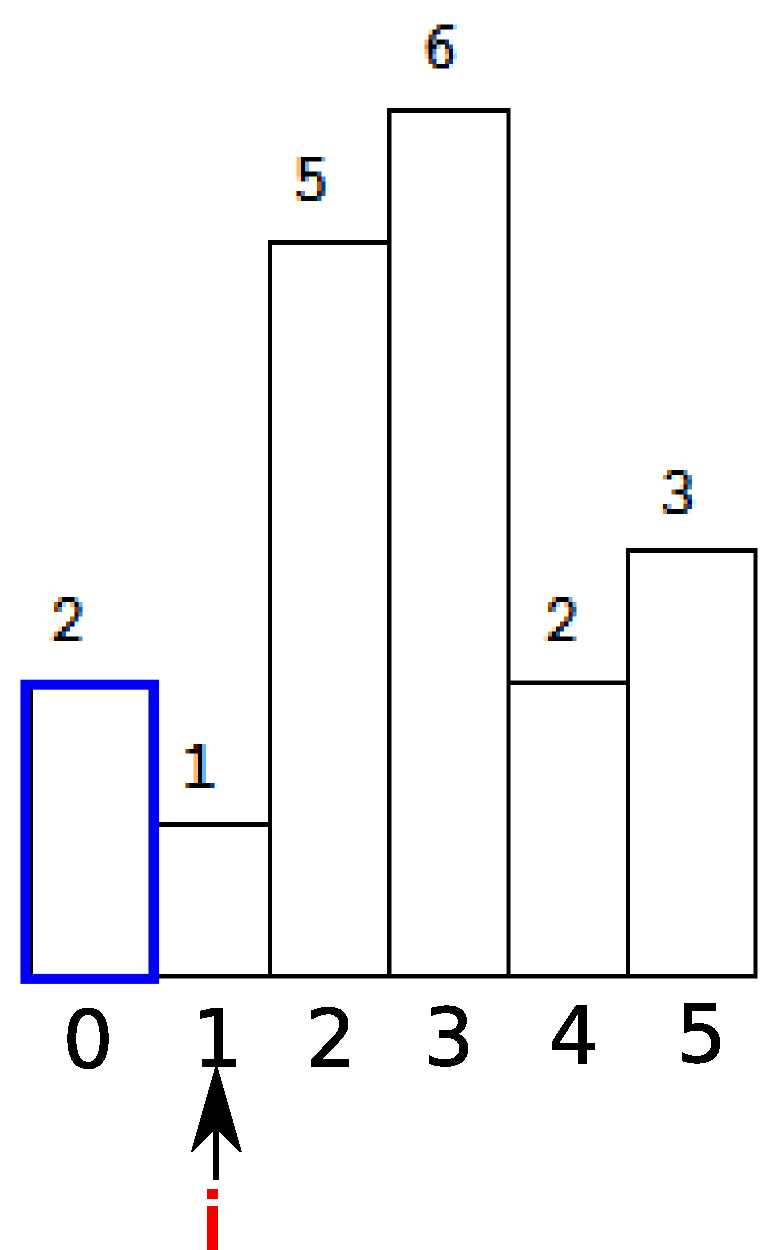
然后继续，当i=1的时候，发现h[i]小于了栈内的元素，于是出栈。（由此可以想到，哦，看来stack里面只存放单调递增的索引）

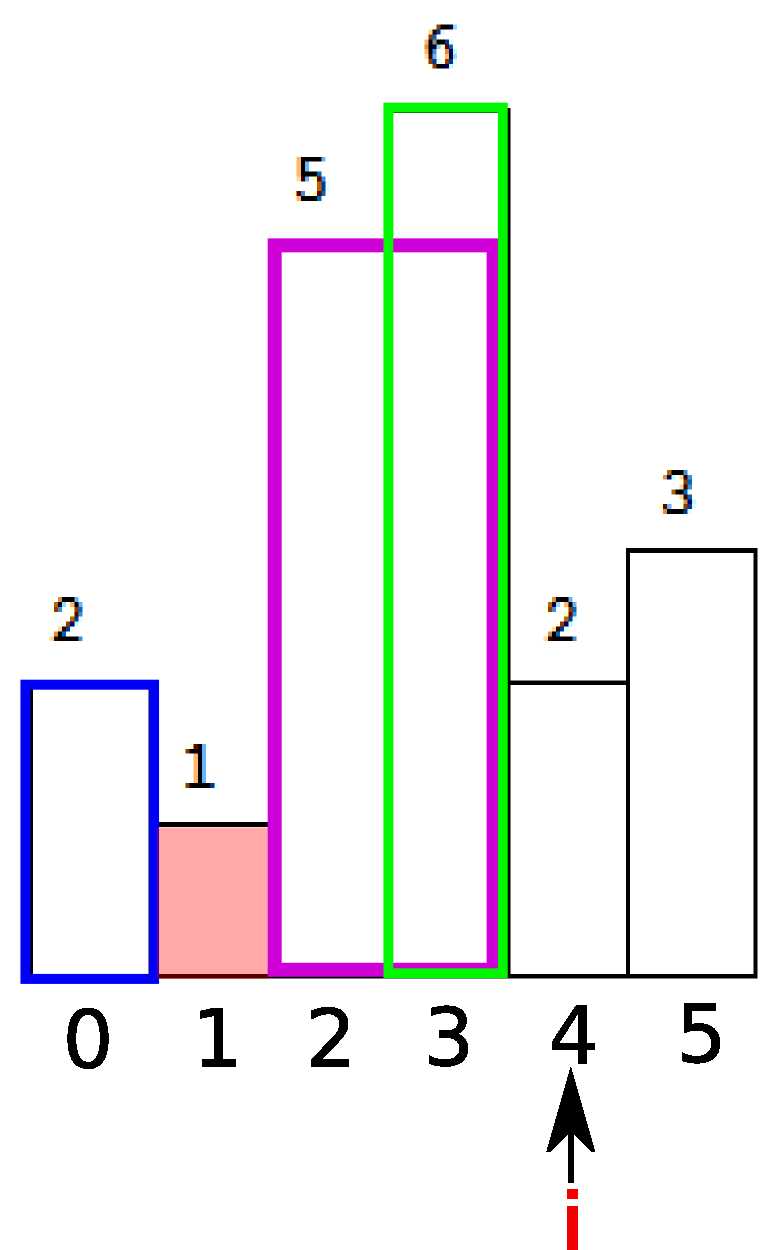
这时候stack为空，所以面积的计算是h[t] * i.t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。

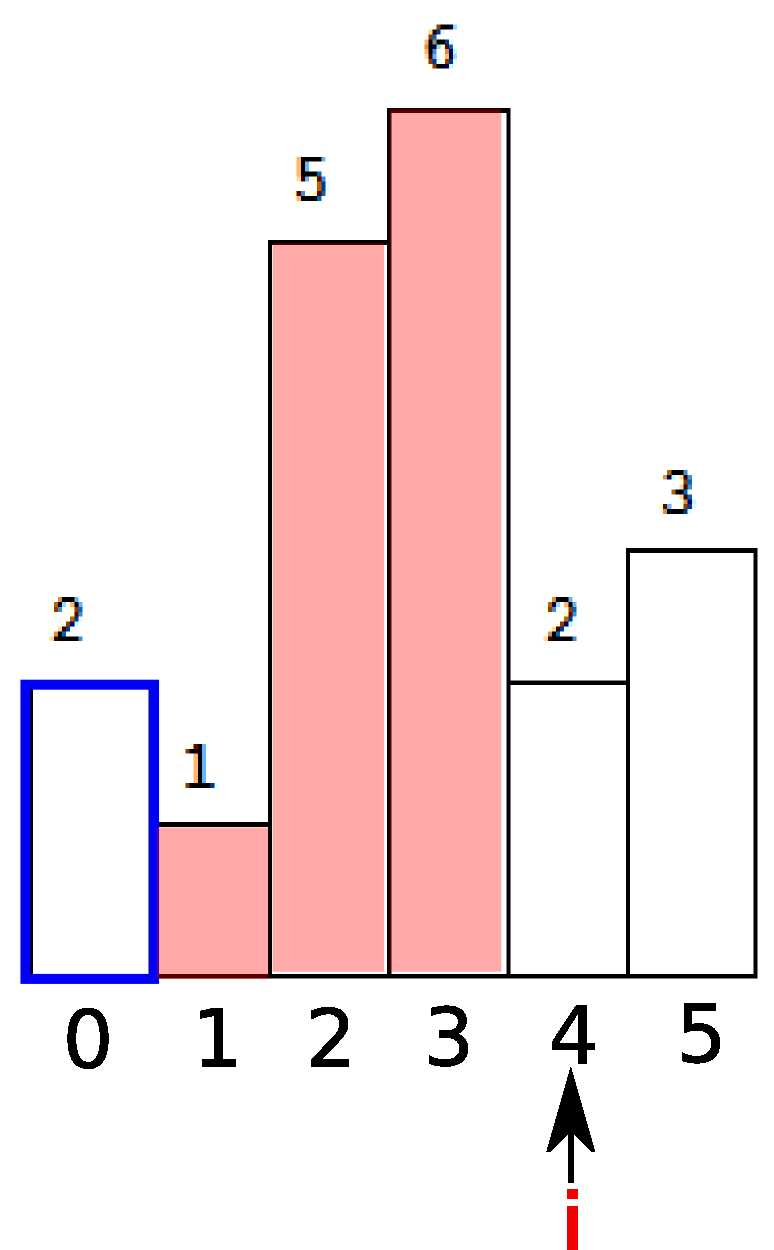
继续。这时候stack为空了，继续入栈。注意到只要是连续递增的序列，我们都要keep pushing，直到我们遇到了i=4，h[i]=2小于了栈顶的元素。

这时候开始计算矩形面积。首先弹出栈顶元素，t=3。即下图绿色部分。

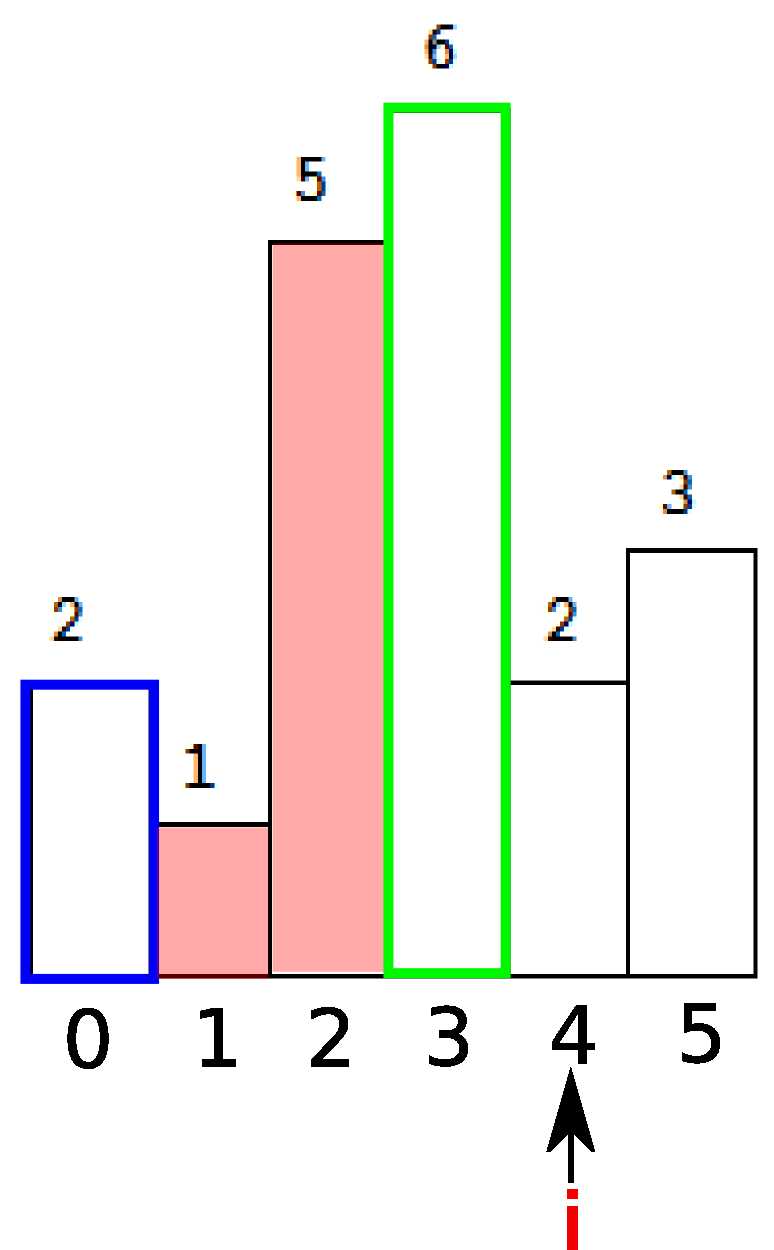
接下来注意到栈顶的（索引指向的）元素还是大于当前i指向的元素，于是出栈，并继续计算面积，桃红色部分。

最后，栈顶的（索引指向的）元素大于了当前i指向的元素，循环继续，入栈并推动i前进。直到我们再次遇到下降的元素，也就是我们最后人为添加的dummy元素0.

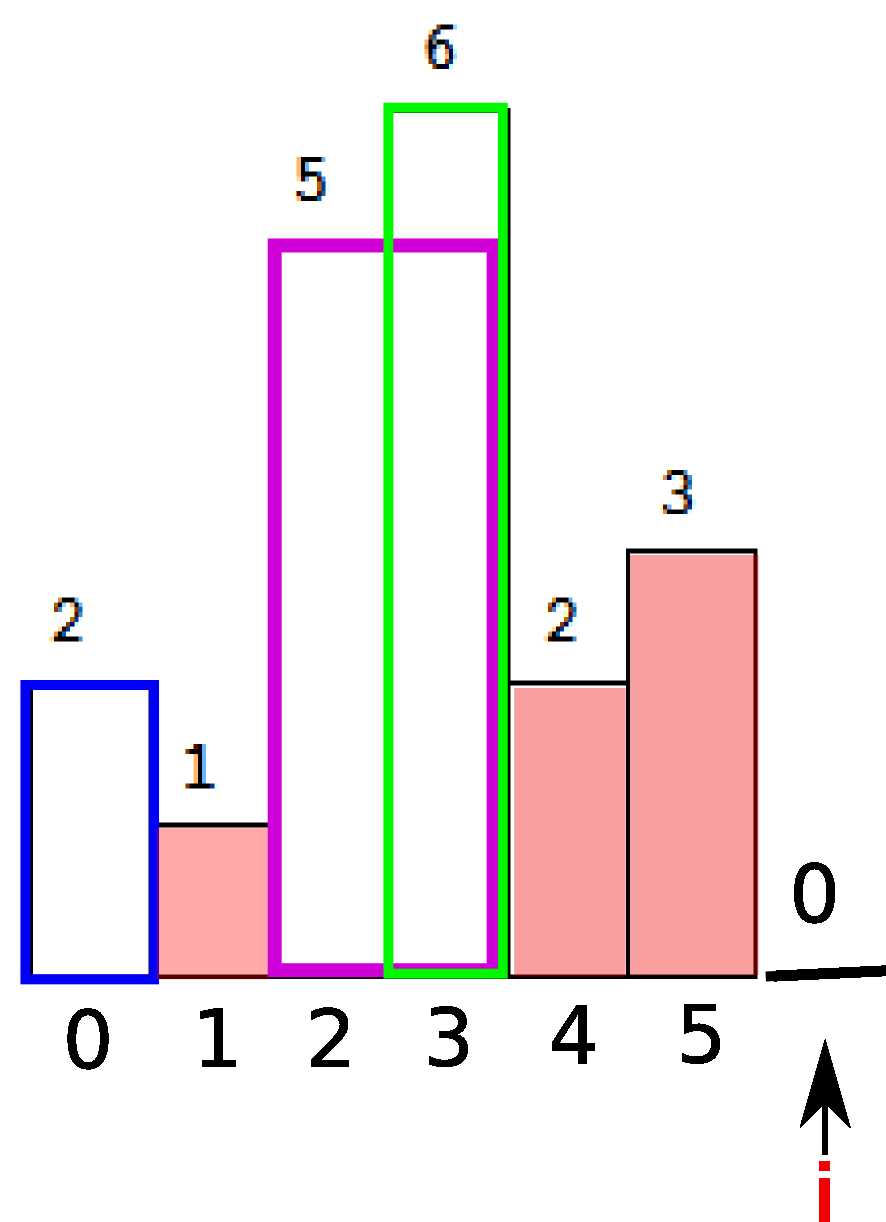
同理，我们计算栈内的面积。由于当前i是最小元素，所以所有的栈内元素都要被弹出并参与面积计算。

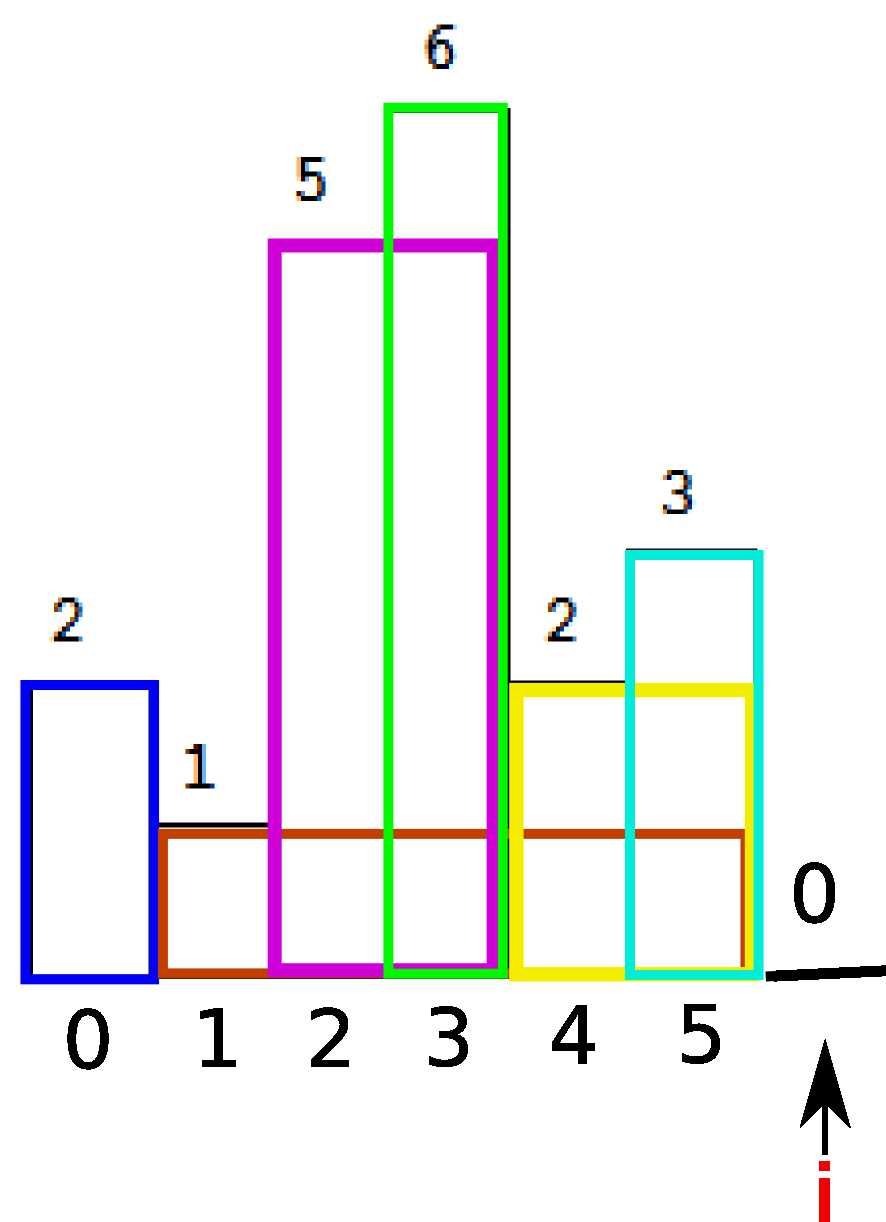
注意我们在计算面积的时候已经更新过了maxArea。

总结下，我们可以看到，stack中总是保持递增的元素的索引，然后当遇到较小的元素后，依次出栈并计算栈中bar能围成的面积，直到栈中元素小于当前元素。

可是为什么这个方法是正确的呢？ 我也没搞清楚。只是觉得不明觉厉了。

 -------------------------------------------------更新----------------------------------------------------------------

可以这样理解这个算法，看下图。

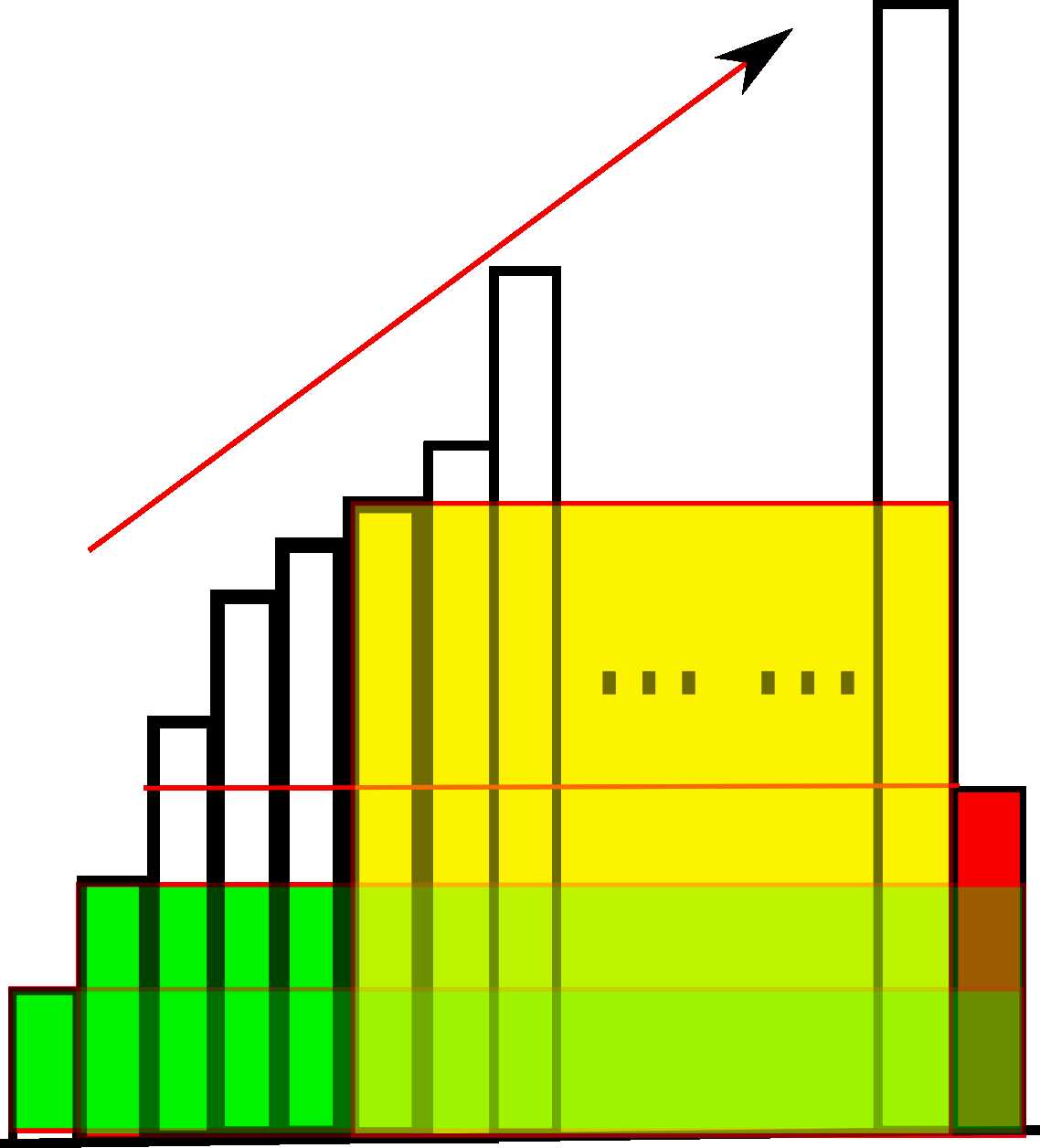
例如我们遇到最后遇到一个递减的bar（红色）。高度位于红线上方的（也就是算法中栈里面大于最右bar的）元素，他们是不可能和最右边的较小高度bar围成一个比大于在弹栈过程中的矩形面积了（黄色面积），因为红色的bar对他们来说是一个短板，和红色bar能围成的最大面积也就是红色的高度乘以这些“上流社会”所跨越的索引范围。但是“上流社会”的高度个个都比红色bar大，他们完全只计算彼此之间围成的面积就远远大于和红色bar围成的任意面积了。所以红色bar是不可能参与“上流社会”的bar的围城的（好悲哀）。

但是屌丝也不用泄气哦。因为虽然长度不占优势，但是团结的力量是无穷的。它还可以参与“比较远的”比它还要屌丝的bar的围城。他们的面积是有可能超过上流社会的面积的，因为距离啊！所以弹栈到比红色bar小就停止了。

另外一个细节需要注意的是，弹栈过程中面积的计算。

h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1)

h[t]是刚刚弹出的栈顶端元素。此时的面积计算是h[t]和前面的“上流社会”能围成的最大面积。这时候要注意哦，栈内索引指向的元素都是比h[t]小的，如果h[t]是目前最小的，那么栈内就是空哦。而在目前栈顶元素和h[t]之间（不包括h[t]和栈顶元素），都是大于他们两者的。如下图所示：

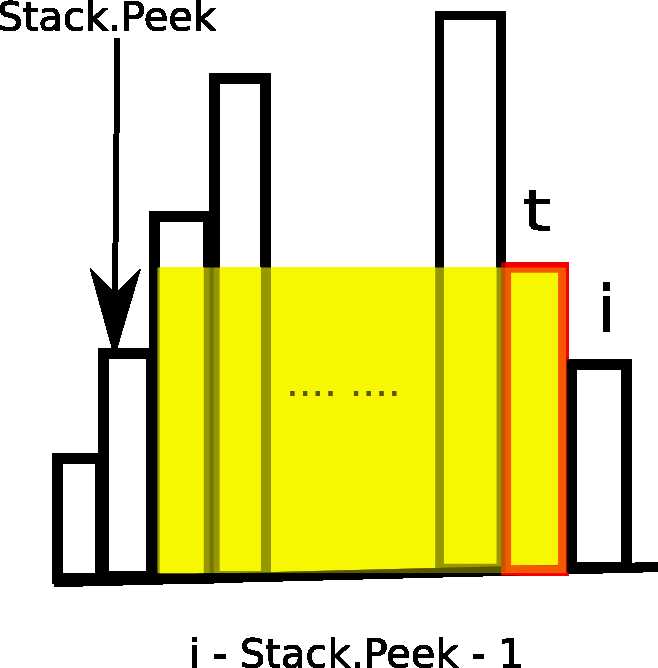
那h[t]无疑就是Stack.Peek和t之间那些上流社会的短板啦，而它们的跨越就是i - Stack.Peek - 1。

所以说，这个弹栈的过程也是维持程序不变量的方法啊：栈内元素一定是要比当前i指向的元素小的。

=============引用结束=============

我自己的code

leetcode 改了东西，所以只能用以前的版本了，懒得跟着改了

public class Solution {
    public int largestRectangleArea(int[] height) {
        int i = 0;
        int res = 0;
        Stack<Integer> st = new Stack<Integer>();
        //padding a new array
        int[] h = new int[height.length+1];
        h = Arrays.copyOf(height, height.length+1); //copyOf(byte[] original, int newLength) Copies the specified array, truncating or padding with zeros (if necessary) so the copy has the specified length.
        
        while(i<h.length){
            if(st.isEmpty() ||h[i] >= h[st.peek()] ){ // 单调递增stack，存储的是index
             // if(st.isEmpty() ||h[i] >= st.peek() ){
                st.push(i++);
            }else{
                int t = st.pop();           // 发现了比我高的，那就在st里往前退回一步
                res = Math.max(res, h[t]*(st.isEmpty()? i: i-st.peek()-1)); // i-st.peek()这个位置是st里面比h【t】矮的那个点，这个点之后到当前i，都比h【t】高，因此面积就是h【t】*i-st.peek()-1
            }
        }
        return res;
    }
}

Largest Rectangle in Histogram

标签：

原文地址：http://www.cnblogs.com/jiajiaxingxing/p/4434405.html