标签:
一、题目和要求
二、设计思路
基本实现其实可以采用枚举法,即每到一个楼层,就要计算出所有人上下的情况,最后比较所有计算出的结果,求出理想楼层,但是,如果采用枚举法,代码时间复杂度较高,为O(n^2),其实可以考虑通过计算普遍情况推广,假设停在第i层,上下楼梯总数为nMinFloor,那么通过对第i-1层和i+1层的计算,就可以计算出最佳楼层。
具体设计思路:假设电梯停在第i层,已知目的楼层在i层的有N2人,在i层以下的有N1人,在x层以上的有N3人。 此时总花费为nMinFloor。则往上走一层的话,总花费变为nMinFloor + N2 + N1 - N3。那么初始状态电梯停在第一层,向上进行状态的变迁,开始时N2 + N1 - N3 < 0。nMinFloor越来越小,直到某一层N2 + N1 >= N3。
三、源代码
1 // Floor.cpp : 电梯调度问题 2 // 3 4 #include "stdafx.h" 5 #include <iostream> 6 using namespace std; 7 int main() 8 { 9 int N = 18; 10 int nPerson[19]; 11 int nMinFloor,nTargetFloor; 12 int N1,N2,N3; //N1表示当前层以下的人数,N2表示当前层人数,N3表示当前层以上人数 13 nTargetFloor = 1; //起始位置为一层 14 cout<<"请输入到达每层的乘客人数(1-18层):"<<endl; 15 nPerson[0]=0; 16 for(int i=1;i<=N;i++) 17 { 18 cin>>nPerson[i]; 19 } 20 N1 = N3 = nMinFloor = 0; 21 N2 = nPerson[1]; 22 //得到nTargetFloor等于1时各变量的值 23 for(int i = 2; i <= N; i++) 24 { 25 N3 += nPerson[i]; //当前层以上的人数 26 nMinFloor += nPerson[i] * (i-1); //总共所需要的楼层数 27 } 28 /* 29 假设电梯停在第i层,已知目的楼层在i层的有N2人,在i层以下的有N1人,在x层以上的有N3人。 30 此时总花费为nMinFloor。则往上走一层的话,总花费变为nMinFloor + N2 + N1 - N3。 31 那么初始状态电梯停在第一层,向上进行状态的变迁,开始时N2 + N1 - N3 < 0。 32 nMinFloor越来越小,直到某一层N2 + N1 >= N3 33 */ 34 for(int i=2;i<=N;i++) 35 { 36 if(N1 + N2 < N3) 37 { 38 nTargetFloor = i; //当前停的楼层数 39 nMinFloor += (N1 + N2 - N3); //最小楼层数 40 N1 += N2; //每次变化楼层,相应楼层人数发生变化 41 N2 = nPerson[i]; 42 N3 -= nPerson[i]; 43 } 44 else 45 { 46 break; 47 } 48 } 49 cout<<"所停楼层:"<<nTargetFloor<<endl; 50 cout<<"最小楼层数:"<<nMinFloor<<endl; 51 return 0; 52 }
四、实验结果
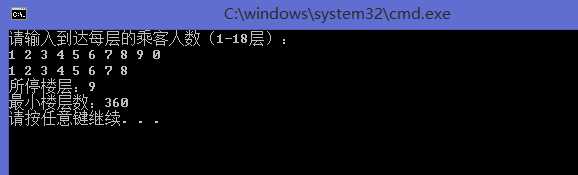
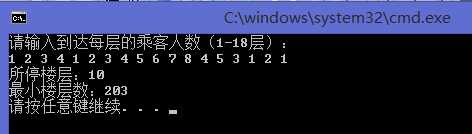
五、实验分析
看到这道题,最简单的想法是穷举,只要计算出每种情况比较就可以了,但是,真的只需要穷举就能满足要求?不能,穷举虽然是一种实用的解决方法,但是,他的复杂度就成了问题,这不是我们想要的最优结果。那么,我们就需要代码优化。优化的过程中,起初我是没有思路的,但是通过老师的引导还有与别人的讨论,渐渐有了头绪。我想说的,不是要去怎么实现代码的优化,而是怎么分析问题,才能将一个复杂的问题具体化,然后具体到某一部分怎么去实现。只有看到了问题的本质,才能找到更好的解决方法。那么如何去正确的分析问题,我认为这是一个过程,首先要做的就是对问题解决有一个基本的解决思路,然后找到这个解决方案的关键点所在,那么再去分析这个关键点,就很容易找到问题所反映出的根本问题。
标签:
原文地址:http://www.cnblogs.com/zhshto/p/4437193.html