标签:
这两种方法都是KL变换的一种形式吧,PCA主要是把高位数据投影到k个低维的正交坐标轴上,来实现尽量保留原始信息
LDA主要是类内与类外的散列程度,该方法投影后的坐标轴不一定正交(因为scatter矩阵不一定是对角的)
两种方法都会转化为求解矩阵特征值特征向量,而且是选择最大的K个特征值对应的特征向量
PCA选最大意味着在这K个轴中散列正度越大,LDA为什么选最大还有待考证
引用一张图:
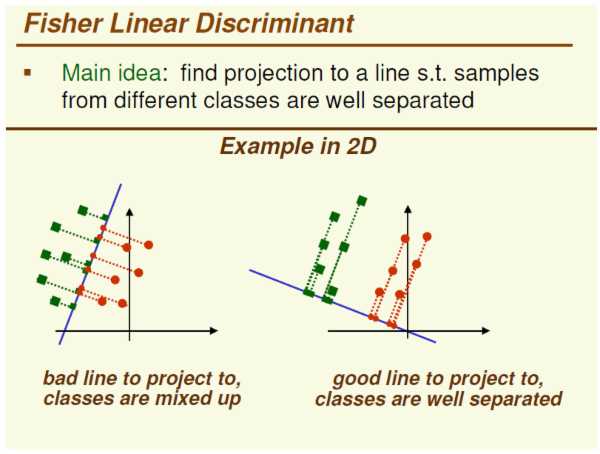
图的左边是PCA,它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据内部的分类信息。
因此,虽然做了PCA后,整组数据在表示上更加方便(降低了维数并将信息损失降到最低),但在分类上也许会变得更加困难。
图的右边是LDA,可以明显看出,在增加了分类信息之后,两组输入映射到了另外一个坐标轴上,有了这样一个映射,两组数据之间的就变得更易区分了(在低维上就可以区分,减少了很大的运算量)。
PCA 是无监督的, 它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有 利用任何数据内部的分类信息。
线性代数真奇妙!!
标签:
原文地址:http://www.cnblogs.com/ooon/p/4437801.html