标签:
八皇后是一个经典问题,在8*8的棋盘上放置8个皇后,每一行不能互相攻击。
因此 拓展出 N皇后问题。
下面慢慢了解解决这些问题的方法:
回溯法:
回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
在现实中,有很多问题往往需要我们把其所有可能穷举出来,然后从中找出满足某种要求的可能或最优的情况,从而得到整个问题的解。
回溯算法就是解决这种问题的“通用算法”,有“万能算法”之称。
N皇后问题在N增大时就是这样一个解空间很大的问题,所以比较适合用这种方法求解。这也是N皇后问题的传统解法,很经典。
算法描述:
1. 算法开始,清空棋盘。当前行设为第一行,当前列设为第一列。
2. 在当前行,当前列的判断放置皇后是否安全,若不安全,则跳到第四步。
3. 在当前位置上满足条件的情况:
在当前位置放一个皇后,若当前行是最后一行,记录一个解;
若当前行不是最后一行,当前行设为下一行,当前列设为当前行的第一个待测位置;
若当前行是最后一行,当前列不是最后一列,当前列设为下一列;
若当前行是最后一行,当前列是最后一列,回溯,即清空当前行以及以下各行的棋盘,然后当前行设为上一行,当前列设为当前行的下一个待测位置;
以上返回第二步。
4.在当前位置上不满足条件:
若当前列不是最后一列,当前列设为下一列,返回到第二步;
若当前列是最后一列,回溯,即,若当前行已经是第一行了,算法退出,否则,清空当前行以及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置,返回第二步。
如何判断是否安全:
把棋盘存储为一个N维数组a[N],数组中第i个元素的值代表第i行的皇后位置,
这样便可以把问题的空间规模压缩为一维O(N),在判断是否冲突时也很简单,
首先每行只有一个皇后,且在数组中只占据一个元素的位置,行冲突就不存在了,
其次是列冲突,判断一下是否有a[i]与当前要放置皇后的列j相等即可。
至于斜线冲突,通过观察可以发现所有在斜线上冲突的皇后的位置都有规律即它们所在的行列互减的绝对值相等,即| row – i | = | col – a[i] | 。这样某个位置是否可以放置皇后的问题已经解决。
递归的方法:
void queen(int row) { if (n == row) //如果已经找到结果,则打印结果 print_result(); else { for (k=0 to N) { //试探第row行每一个列 if (can_place(row, k) { place(row, k); //放置皇后 queen(row + 1); //继续探测下一行 } } }
该方法由于在探测第i行后,如果找到一个可以放置皇后的位置j后,则会递归探测下一行,
结束后则会继续探测i行j+1列,故可以找到所有的N皇后的解。
非递归:
非递归方法的一个重要问题时何时回溯及如何回溯的问题。
程序首先对N行中的每一行进行探测,寻找该行中可以放置皇后的位置,具体方法是对该行的每一列进行探测,看是否可以放置皇后,如果可以,则在该列放置一个皇后,然后继续探测下一行的皇后位置。
如果已经探测完所有的列都没有找到可以放置皇后的列,此时就应该回溯,把上一行皇后的位置往后移一列,如果上一行皇后移动后也找不到位置,则继续回溯直至某一行找到皇后的位置或回溯到第一行,如果第一行皇后也无法找到可以放置皇后的位置,则说明已经找到所有的解程序终止。
如果该行已经是最后一行,则探测完该行后,如果找到放置皇后的位置,则说明找到一个结果,打印出来。但是此时并不能再此处结束程序,因为我们要找的是所有N皇后问题所有的解,此时应该清除该行的皇后,从当前放置皇后列数的下一列继续探测。
1 //八皇后问题:回溯法(非递归) 2 void Queens8() 3 { 4 int n = 8; //8个皇后 5 int count = 0; //记录当前第几情况 6 int a[9] = {0}; //存放皇后位置,如:a[2] = 4;表示第2列第4行有一个皇后(a[0]不用) 7 int i = 0,k = 1; //初始化k为第一列 8 9 a[1] = 0; //初始化a[1] = 0 10 11 while (k > 0) //k==0时:表示摆放第1个皇后就超过了列底部(即已经找完所有情况) 12 { 13 a[k] += 1; //a[k]位置,摆放一个皇后 14 while ((a[k] <= n) && (!Chongtu(a,k)))//如果a[k](即皇后摆放位置)没有到列最底部,且摆放冲突。 15 a[k] += 1;//将皇后列下移一位 16 if (a[k] <= n)//皇后摆放位置没有到达列最底部 17 { 18 if (k == n)//k==n表示,8列皇后全部摆放完毕 19 { 20 printf("第%d种情况:",++count); 21 for (i = 1; i <= n; ++i)//打印情况 22 printf("%d ",a[i]); 23 printf("\n"); 24 } 25 else //皇后还未摆放完毕 26 { 27 k += 1; //继续摆放下一列 28 a[k] = 0; //此行初始化a[k] = 0;表示第k列,从第一行开始摆放皇后 29 } 30 } 31 else //回溯:当a[k]>8进入else,表示在第k列中没有找到合适的摆放位置 32 k -= 1;//回溯到k-1步:k表示第几个皇后,a[k]表示第k个皇后摆放的位置 33 } 34 return; 35 } 36 37 //主函数 38 int main() 39 { 40 Queens8(); 41 42 return 0; 43 }
目前非常高效的算法:
1 void test(int row, int ld, int rd) 2 { 3 int pos, p; 4 if ( row != upperlim ) 5 { 6 pos = upperlim & (~(row | ld | rd )); 7 while ( pos ) 8 { 9 p = pos & (~pos + 1); 10 pos = pos - p; 11 test(row | p, (ld | p) << 1, (rd | p) >> 1); 12 } 13 } 14 else 15 ++Ans; 16 }
初始化: upperlim = (1 << n)-1; Ans = 0;
调用参数:test(0, 0, 0);
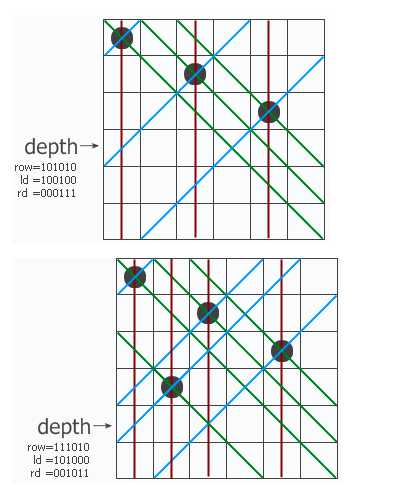
和普通算法一样,这是一个递归函数,程序一行一行地寻找可以放皇后的地方。函数带三个参数row、ld和rd,分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来,得到该行所有的禁位,取反后就得到所有可以放的位置(用pos来表示)。
p = pos & (~pos + 1)其结果是取出最右边的那个1。这样,p就表示该行的某个可以放子的位置,把它从pos中移除并递归调用test过程。
注意递归调用时三个参数的变化,每个参数都加上了一个禁位,但两个对角线方向的禁位对下一行的影响需要平移一位。最后,如果递归到某个时候发现row=upperlim了,说明n个皇后全放进去了,找到的解的个数加一。
注:
upperlime:=(1 << n)-1 就生成了n个1组成的二进制数。
这个程序是从上向下搜索的。
pos & -pos 的意思就是取最右边的 1 再组成二进制数,相当于 pos &(~pos +1),因为取反以后刚好所有数都是相反的(怎么听着像废话),再加 1 ,就是改变最低位,如果低位的几个数都是1,加的这个 1 就会进上去,一直进到 0 ,在做与运算就和原数对应的 1 重合了。举例可以说明:
原数 0 0 0 0 1 0 0 0 原数 0 1 0 1 0 0 1 1
取反 1 1 1 1 0 1 1 1 取反 1 0 1 0 1 1 0 0
加1 1 1 1 1 1 0 0 0 加1 1 0 1 0 1 1 0 1
与运算 0 0 0 0 1 0 0 0 and 0 0 0 0 0 0 0 1
其中呢,这个取反再加 1 就是补码,and 运算 与负数,就是按位和补码与运算。
(ld | p)<< 1 是因为由ld造成的占位在下一行要右移一下;
(rd | p)>> 1 是因为由rd造成的占位在下一行要左移一下。
ld rd row 还要和upperlime 与运算 一下,这样做的结果就是从最低位数起取n个数为有效位置,原因是在上一次的运算中ld发生了右移,如果不and的话,就会误把n以外的位置当做有效位。
pos 已经完成任务了还要减去p 是因为?
while 循环是因为?
在进行到某一层的搜索时,pos中存储了所有的可放位置,为了求出所有解,必须遍历所有可放的位置,而每走过一个点必须要删掉它,否则就成死循环啦!
这个是目前公认N皇后的最高效算法。
1 /* 2 ** 目前最快的N皇后递归解决方法 3 ** N Queens Problem 4 ** 试探-回溯算法,递归实现 5 */ 6 #include "iostream" 7 using namespace std; 8 #include "time.h" 9 10 // sum用来记录皇后放置成功的不同布局数;upperlim用来标记所有列都已经放置好了皇后。 11 long sum = 0, upperlim = 1; 12 13 // 试探算法从最右边的列开始。 14 void test(long row, long ld, long rd) 15 { 16 if (row != upperlim) 17 { 18 // row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0, 19 // 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列改为1 20 // 也就是求取当前哪些列可以放置皇后 21 long pos = upperlim & ~(row | ld | rd); 22 while (pos) // 0 -- 皇后没有地方可放,回溯 23 { 24 // 拷贝pos最右边为1的bit,其余bit置0 25 // 也就是取得可以放皇后的最右边的列 26 long p = pos & -pos; 27 28 // 将pos最右边为1的bit清零 29 // 也就是为获取下一次的最右可用列使用做准备, 30 // 程序将来会回溯到这个位置继续试探 31 pos -= p; 32 33 // row + p,将当前列置1,表示记录这次皇后放置的列。 34 // (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。 35 // (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。 36 // 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归 37 // 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位 38 // 在每次选择列之前进行,原来N×N网格中某个已放置的皇后针对其对角线 39 // 上产生的限制都被记录下来了 40 test(row + p, (ld + p) << 1, (rd + p) >> 1); 41 } 42 } 43 else 44 { 45 // row的所有位都为1,即找到了一个成功的布局,回溯 46 sum++; 47 } 48 } 49 50 int main(int argc, char *argv[]) 51 { 52 time_t tm; 53 int n = 16; 54 55 if (argc != 1) 56 n = atoi(argv[1]); 57 tm = time(0); 58 59 // 因为整型数的限制,最大只能32位, 60 // 如果想处理N大于32的皇后问题,需要 61 // 用bitset数据结构进行存储 62 if ((n < 1) || (n > 32)) 63 { 64 printf(" 只能计算1-32之间\n"); 65 exit(-1); 66 } 67 printf("%d 皇后\n", n); 68 69 // N个皇后只需N位存储,N列中某列有皇后则对应bit置1。 70 upperlim = (upperlim << n) - 1; 71 72 test(0, 0, 0); 73 printf("共有%ld种排列, 计算时间%d秒 \n", sum, (int) (time(0) - tm)); 74 system("pause"); 75 return 0; 76 }
上述代码还是比较容易看懂的,但我觉得核心的是在针对试探-回溯算法所用的数据结构的设计上。
程序采用了递归,也就是借用了编译系统提供的自动回溯功能。
算法的核心:使用bit数组来代替以前由int或者bool数组来存储当前格子被占用或者说可用信息,从这可以看出N个皇后对应需要N位表示。
巧妙之处在于:以前我们需要在一个N*N正方形的网格中挪动皇后来进行试探回溯,每走一步都要观察和记录一个格子前后左右对角线上格子的信息;采用bit位进行信息存储的话,就可以只在一行格子也就是(1行×N列)个格子中进行试探回溯即可,对角线上的限制被化归为列上的限制。
程序中主要需要下面三个bit数组,每位对应网格的一列,在C中就是取一个整形数的某部分连续位即可。 row用来记录当前哪些列上的位置不可用,也就是哪些列被皇后占用,对应为1。ld,rd同样也是记录当前哪些列位置不可用,但是不表示被皇后占用,而是表示会被已有皇后在对角线上吃掉的位置。这三个位数组进行“或”操作后就是表示当前还有哪些位置可以放置新的皇后,对应0的位置可放新的皇后。如下图所示的8皇后问题求解得第一步:
row: [ ][ ][ ][ ][ ][ ][ ][*]
ld: [ ][ ][ ][ ][ ][ ][*][ ]
rd: [ ][ ][ ][ ][ ][ ][ ][ ]
--------------------------------------
row|ld|rd: [ ][ ][ ][ ][ ][ ][*][*]
所有下一个位置的试探过程都是通过位操作来实现的,这是借用了C语言的好处,详见代码注释。
关于此算法,如果考虑N×N棋盘的对称性,对于大N来说仍能较大地提升效率!
位操作--对优化算法有了个新的认识
这个是在csdn找到的一个N皇后问题最快的算法,看了好一会才明白,这算法巧妙之处我认为有2个:
1、以前都是用数组来描述状态,而这算法采用是的位来描述,运算速度可以大大提升,以后写程序对于描述状态的变量大家可以借鉴这个例子,会让你的程序跑得更快
2、描述每行可放置的位置都是只用row,ld,rd这3个变量来描述,这样使得程序看起来挺简洁的。
感谢
http://blog.csdn.net/hackbuteer1/article/details/6657109
在学习的道路上不断学习他人的总结。
标签:
原文地址:http://www.cnblogs.com/jawiezhu/p/4437875.html