标签：
转载
1、基于加窗DFT变换域处理算法
接收机接收到的信号由期望信号、信道噪声和窄带干扰信号3部分组成，可以写成数学表达式：
r(t) = s(t) + g(t) + j(t) (1)
其中，s(t)为数据序列经过伪随机码扩频之后，进行BPSK调制得到的发射信号，g(t)为零均值，双边功率谱密度为N0/2的加性高斯白噪声，j(t)为窄带干扰信号。
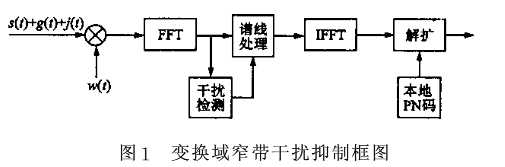
图1为基于加窗DFT窄带干扰抑制接收机原理图。首先对接收信号进行加窗，然后经过快速傅里叶变换，对变换后的谱线进行干扰检测，将存在干扰的谱线置零或者衰减至与背景噪声相当的程度，以达到减轻和抑制窄带干扰的目的。对经过滤波处理之后的谱线进行逆快速傅里叶变换(IFFT)回到时域，与本地PN码相关运算，经过判决器得到发送的信息序列。
2、信号加窗与恢复
DFT变换隐含了对长度为N的截断序列进行拓展，如果截断后序列在边界不连续，则会导致信号经过DFT变换之后出现能量泄露，从而使得窄带干扰信号的能量对临近的频谱产生严重的“污染”，为了减轻DFT变换的能量泄露，常用的方法是在对信号进行DFT之前进行加窗，窗函数的引入使得截断序列的边界变得平滑，因此可以减轻DFT的能量泄露问题。
另一方面，窗函数的引入也使得信号波形产生失真，通常用信号的信噪比损失来衡量加窗对信号的影响，假定窗函数的系数为：
{w(n), n = 0, 1, 2,..., N-1}。
则定义加窗引入的信噪比损失为:
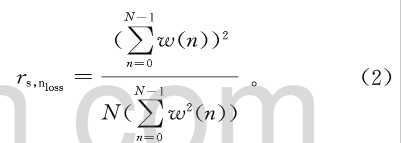
常用的Hamming窗，其旁瓣为-31dB，引入的信噪比损失为1.36dB，而Blackman窗，其旁瓣为-60dB，引入的信噪比损失为2.7dB。通过选择旁瓣较低的窗函数，可以将窄带干扰信号的大部分能量限定在有限的几根谱线之内，从而减小需要抑制的谱线的根数，最大程度地减小对期望信号的失真。对于不是很强的窄带干扰信号，通过加Hamming窗可以将窄带干扰的能量集中在有限的谱线内。但是干扰信号较强时，仍然有较大的旁瓣，会对临近的信号频谱造成一定的影响，Blackman窗函数的旁瓣抑制效果较好，其旁瓣抑制可以达到-60dB，考虑到系统工作环境比较恶劣，可以选择Blackman窗函数对序列进行加窗。
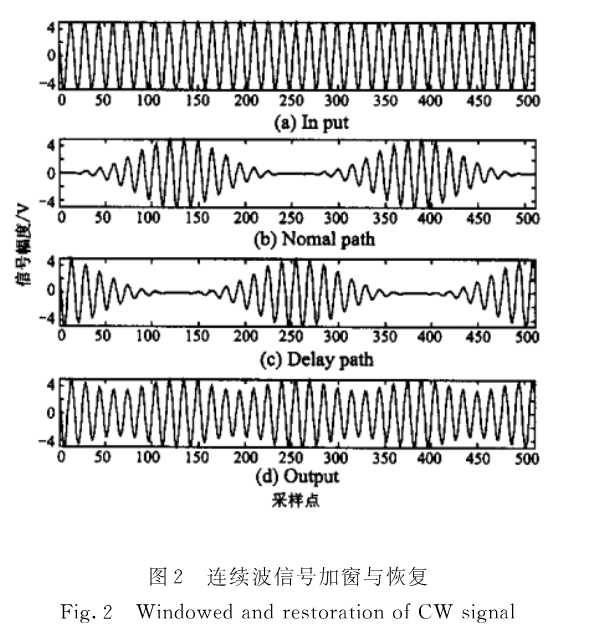
以上分析可知，对接收信号加窗将使得接收信号产生失真，如图2所示，从而使得信号信噪比下降，为了减轻加窗对信号波形产生的失真，可以通过在相临的变换截断序列之间存在50%重叠的方法来减弱加窗对信号波形的失真。
如图3所示，对输入序列进行截断时，相临2块之间存在50%的重叠，2块截断序列分别与等长度的Blackman窗函数相乘，之后进行FFT变换，经过频域滤波处理之后，进行FFT反变换，然后将2个相邻的截断序列中重叠的部分相加，得到输出序列。
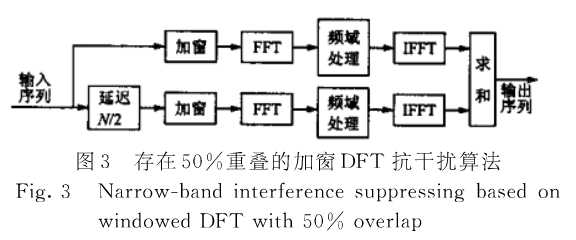
图2(a)为输入序列的波形图，图2(b)为没有重叠情况下进行加窗FFT之后，恢复得到的信号波形图，对比图2(a)和图2(b)可以看出，无重叠情况下，恢复得到的信号相对于输入信号波形产生严重的失真，在不考虑频域处理的情况下，这种失真主要是由于时域加窗产生的。图2(d)为存在重叠情况下得到的恢复波形，可以看出，存在重叠的情况下，恢复信号的失真程度大大减小。对于256点Blackman窗，存在50%重叠的情况下，恢复信号的信噪比损失从3dB降低为0.6dB左右。
重叠/相加处理可以减轻加窗产生的信号失真，代价是计算量增加1倍，正常通路和延迟通路的信号都需要进行加窗、FFT、频域处理以及FFT反变换，最后对2个序列进行求和，对系统进行的硬件设计时，其所需要的硬件资源增加1倍。可见，重叠/相加减小加窗引入的信号失真是以增加系统复杂度为代价的。
3、频域干扰检测与处理方法
在DSSS系统中，接收到的信号由于经过PN码扩频之后的序列相关性很小，可以近似看成是一个白噪声，信道噪声g(n)是服从高斯分布的白噪声。在扩展比较大的情况下，由于信号的功率远远小于噪声的功率（在GPS接收机中，信号功率比噪声低20dB左右)，在频谱中表现为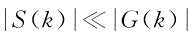
，而DFT变换等效于将信号通过一组中心频率为2*pi*k/N，(k=0,1,2, ... , N-1)，频率响应为sin(Nx)/sin(x)的窄带滤波器组，X(k)即输入序列x(n)经过第k个滤波器在(N-1)时刻的输出。因此，高斯白噪声s(n)+g(n)通过一个窄带滤波器在(N-1)时刻的输出值S(k)+G(k)可以看作一个包络服从瑞利分布，包络的平方服从指数分布，相位服从[0,2*pi)的均匀分布窄带高斯随机变量。
假设信道噪声的功率为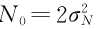
，信号的功率为
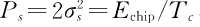，则
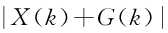服从瑞利分布，且
，
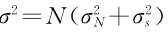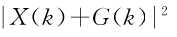服从参数为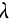
的指数分布，由瑞利分布和指数分布之间的关系可得
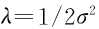。因此，在无窄带干扰情况下，可以认为接收序列经过DFT变换之后得到的N根谱线的幅度平方服从参数为
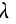指数分布，由指数分布的数字特征可知：
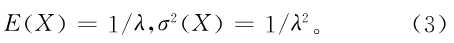
假定在频域干扰检测时取门限T，则记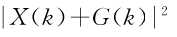
不超过该门限的概率p为：
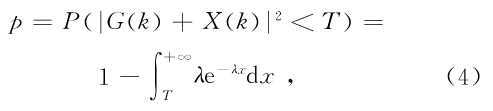
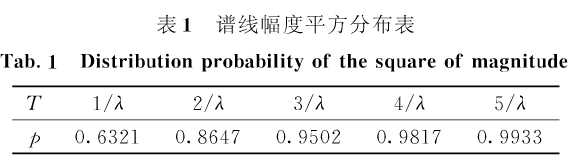
分别取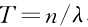
，其中，n=1,2,3,4,5可以得到表1所示的结果。
当FFT变换的点数N较大(N>256)时，可以用谱线幅度平方和的平均值作为平均值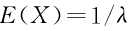
的估计，即：
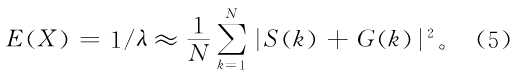
频域进行干扰检测的问题转化为检测N根谱线模的平方分布是否服从指数分布的问题，首先假定序列服从指数分布的假定成立，对谱线的模平方求均值，然后进行统计。根据表1可知，指数分布中X大于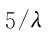
的概率非常小，可以近似认为是不可能发生的小概率事件。因此，认为所有幅度平方值超过门限
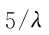的谱线不符合指数分布，可以将其进行裁剪至与均值相当的幅度或置零，然后重新对新的序列进行统计分析。干扰检测与处理算法具体步骤描述如下：
步骤1，求N根谱线模平方的平均值，作为对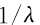
的估计。
步骤2，计算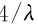
和
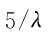的值。
步骤3，对N根谱线进行统计，如果有谱线模平方的值大于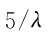
，则认为该组谱线模平方中有不服从指数分布的谱线存在，则对其进行裁剪或则置零。如果采取谱线置零法，则下次统计时要对要对平均值进行适当放大。
步骤4，检查模平方大于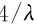
的谱线有没有连续NxP根以上出现的现象，如果出现则认为该段谱线中存在窄带干扰，对该段谱线进行裁剪或置零处理。
步骤5，返回步骤1，对处理之后的谱线再次进行统计，直到无满足步骤3和步骤4处理条件的谱线出现为止。
4、数值仿真与分析
为了检验本文提出算法的性能，我们对其进行Monte Carlo 仿真试验，仿真采用BPSK调制方式，扩频码取周期为63的m序列，每一信息比特被一个完整周期的伪随机码扩频，接收信号按chip速率采样，窗函数采用256点Blackman窗，变换采用重叠50%的加窗256点FFT变换。
图4给出多音干扰（3个单音干扰信号）情况下本文算法的处理效果。其中，3个单音干扰信号的强度均为rj,8 = 24dB，干扰相对载频的归一化频差分别为0.3533,0.55,0.777。图4中，2根虚线分别对应统计平均值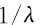
的估计以及自适应门限
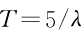。经过5次反复滤波之后，所有谱线的模平方值均没有超过门限，此时，可以认为干扰信号被完全滤除。由表1可知，在无干扰信号存在的情况下，谱线的模平方值超过自适应门限的概率小于0.7%，是小概率事件，一般认为是不可能发生的，因此在没有干扰信号的情况下，该算法不会对有用信号产生不必要的失真，只有在干扰信号存在的情况下，该算法才会被激活，从而可以有效提高系统性能。从硬件实现的角度来看，该算法避免了在FPGA中难以实现的求根运算，计算频域序列的模平方可以通过实部和虚部平方和得到，自适应门限基于模平方和的平均值可直接求出，谱线处理可以通过寄存器清零实现，具有实现简单的优点。
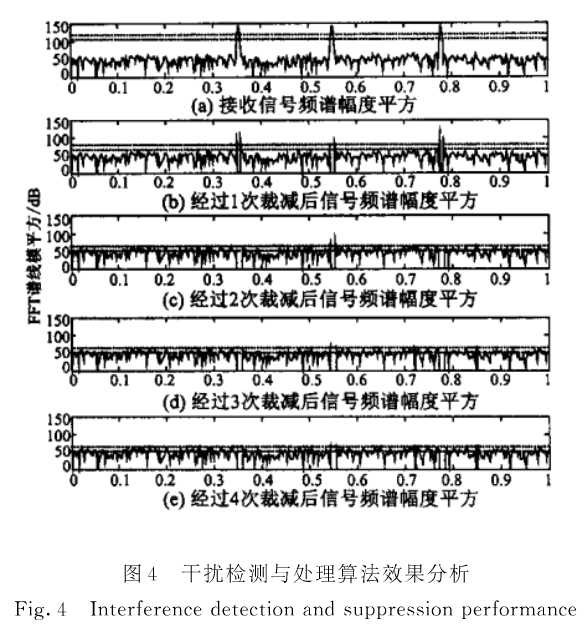
图5给出了接收机在无干扰、单音干扰、多音干扰（3个单音干扰）和AR模型窄带干扰情况下的误码率曲线。为了便于进行性能比较，图中同时给出无干扰时误码率的理论曲线（图中用THE表示）、K谱线法干扰检测和处理法（图中K bins表示）的性能曲线， K谱线法在每次加窗FFT之后，对谱线按模值从大到小进行排序，并将模值最大的K根谱线置零来去除接收信号中的干扰分量，参数K可以根据实际情况取固定值或根据变换域干扰能量的分布情况取最优值。为简单起见，仿真中取K=8，即在256点FFT之后，每次固定将幅度最大的8根谱线进行置零。
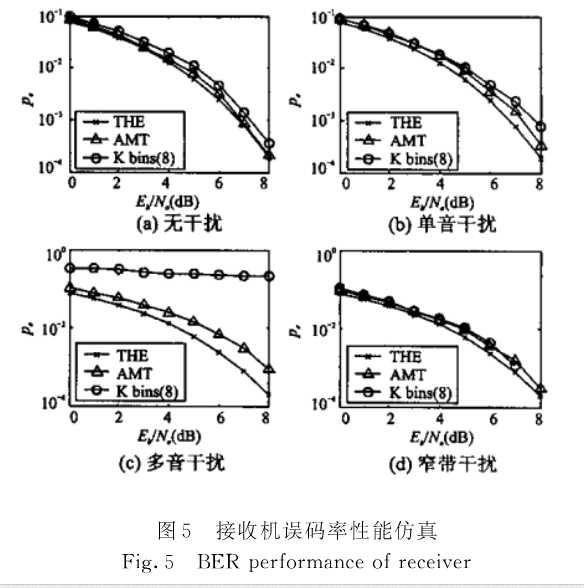
从图5(a)可以看到，在无窄带干扰信号存在时，由于K谱线法将幅度最大的8根谱线进行置零处理，因此对有用信号的能量具有一定的损失。而采用本文提出的自适应多门限检测法进行处理，谱线的模平方值超过门限为小概率事件，因此一般不会在无干扰情况下造成有用信号能量的损失。图5(b)为存在一个rj,s=25dB，归一化频率为0.837的单音干扰时系统的误码率曲线。从图中可以看出，当存在单音干扰时，自适应多门限检测法的性能与K谱线法相当，但当单音干扰很强旁瓣较高时，该算法的性能将明显优于K谱线法。图5(c)为存在3个单音干扰时的情况，3个单音干扰信号的强度分别为rj,s=25dB，15dB，20dB，归一化频率分别为0.3333，0.577，0.84。此时，K谱线法通过抑制幅度最大的8根谱线已经无法有效抑制干扰，自适应多门限检测法则可以有效抑制多音干扰信号。由于需要将谱线模平方值较大的谱线置零，因此抑制干扰的同时，也将相应频带上的有用信号抑制，从而造成一定的信号能量损失。图5(d)为存在AR模型窄带干扰信号时的情况，AR模型参数取
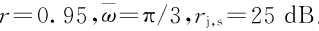。从误码率曲线可以看出，自适应多门限检测法可以有效检测和抑制接收信号中存在的AR模型窄带干扰信号。
标签：
原文地址：http://www.cnblogs.com/fall-li/p/4437695.html
