标签:
上一周我们研究了2xN的骨牌问题,这一周我们不妨加大一下难度,研究一下3xN的骨牌问题?
所以我们的题目是:对于3xN的棋盘,使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢?
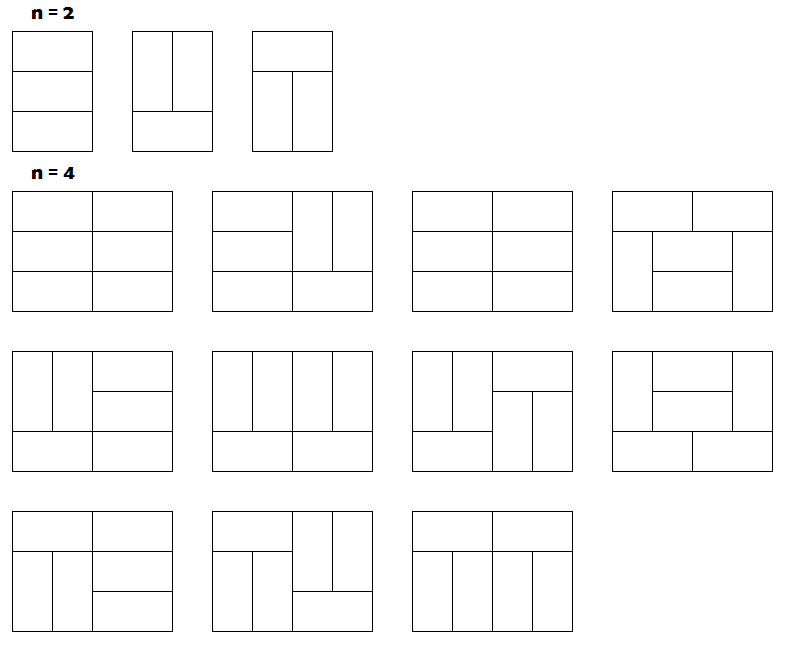
首先我们可以肯定,奇数长度一定是没有办法覆盖的;对于偶数长度,比如2,4,我们有下面几种覆盖方式:
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
第1行:1个整数,表示覆盖方案数 MOD 12357
62247088
4037
#include <iostream>
#include <vector>
using namespace std;
#define modnum 12357
typedef vector<long long> matrow;
typedef vector<matrow> mat;
mat build(long long x,long long y,long long a[])
{
mat ans;
for(long long i=0;i<x;i++)
{
ans.push_back(matrow());
for(long long j=0;j<y;j++)
{
ans[i].push_back(a[i*y+j]);
}
}
return ans;
}
mat multi(const mat mat1,const mat mat2)
{
long long temp=0;
long long rownum=mat1.size();
long long colnum=mat2[0].size();
long long nummul=mat1[0].size();
mat ans;
for(long long i=0;i<rownum;i++)
{
ans.push_back(matrow());
for(long long j=0;j<colnum;j++)
{
temp=0;
for(long long t=0;t<nummul;t++)
temp+=mat1[i][t]*mat2[t][j];
ans[i].push_back(temp%modnum);
}
}
return ans;
}
int main()
{
long long N;
long long a[]={3,1,2,1};
long long b[]={3,2};
cin>>N;
if(N%2==1){ cout<<0<<endl; return 0; }
mat ans=build(2,1,b);
mat temp=build(2,2,a);
long long n=N/2-1;
if(n==0)cout<<3<<endl;
if(n==1)cout<<11<<endl;
if(n!=1&&n!=0)
{
while(n)
{
if(n&1==1)
ans=multi(temp,ans);
temp=multi(temp,temp);
n=n>>1;
}
}
cout<<ans[0][0]<<endl;
return 0;
}
这一期的问题和上一期的一样,也是使用矩阵乘法加速,
用Xn表示N的排列总数
用Tn表示N的特殊排列总数(特殊排列:最后一列有竖直骨牌如:n=2时 第二第三个骨牌。 n=4时2 4 6 7 8 10 11)
N+2的排列总数 = “N的排列总数 拼接上n=2时的排列” + “N的特殊排列 拼接上n=2时第一个骨牌 并进行微调”
( “N的特殊排列 接上n=2时第一个骨牌 并进行微调” 参见n=4时 4和8 ,通过n=4时 9和5调整获得 )
Xn+2=Xn*3+Tn
N+2的特殊排列=“N的排列总数,拼接上n=2时 2 3 骨牌”+ “N的特殊排列 ,拼接上n=2时第一个骨牌 并进行微调”
Tn+2=Xn*2+Tn
用矩阵表示:
|Xn+2m| = |3 1| ^m-1 |3|
|Tn+2m| |2 1| |2|
斐波那契数列 改1 3*N 骨牌覆盖 改1 hiho一下 第四十二周 递归不行 矩阵加速
标签:
原文地址:http://www.cnblogs.com/tjsudys/p/4438831.html