标签:
石家庄铁道大学基础大楼一共有四部电梯,每层都有人上下,电梯在每层都停。信1201-2班的张一东觉得在每层都停觉得不耐烦。由于楼层不太高,在上下课高峰期时时,电梯从一层上行,但只允许停在某一楼层。在一楼时,每个乘客选择自己的目的层,电梯则自动计算出应停的楼层。问电梯停在那一楼层,能够保证这次乘坐电梯的所有乘客爬楼梯的层数之和最少。
思路:
(一):最容易想到的枚举法。从第1层枚举到第N层,假设电梯在第i层停,求出此时所有乘客需要爬多少层楼的总数,看到最少的那层就是答案。
(二):微软公司面试题有类似的,老师上课提到过,假设电梯在第i层停,已知在i层的有N2人,在i层以下的有N1人,在i层以上的有N3人,这时乘客一共要爬Y层。在i+1层停的话,乘客要爬Y + N2 + N1 - N3。这就发现当N2 + N1 - N3 < 0时则更优;在i-1层停同理。
在CSDN论坛上找了相关资料,普遍用思路一实现,用思路二进行更深一步的思考。
源代码:

#define FLOORSNUM 18
#include <iostream.h>
void StopAtOnlyOneFloor_AllFloorWalkLayers(int *_iFloorPassengerNum, int N)
{
int i;
cout<<endl;
cout<<"PassengerNums\tFloor\tWalks"<<endl;
int NBottom=0,NFloor=_iFloorPassengerNum[0],NAbove=0,minWalkLayer=0;
for(i=1;i<N;++i)
{
NAbove+=_iFloorPassengerNum[i];
minWalkLayer=minWalkLayer+(_iFloorPassengerNum[i]*i);
}
cout<<"\t"<<_iFloorPassengerNum[0]<<"\tNo.1\t"<<minWalkLayer<<"Fs"<<endl;
for(i=1;i<N;++i)
{
NAbove=NAbove-_iFloorPassengerNum[i];
NBottom=NBottom+NFloor;
NFloor=_iFloorPassengerNum[i];
minWalkLayer=minWalkLayer-NFloor-NAbove+NBottom;
cout<<"\t"<<_iFloorPassengerNum[i]<<"\tNo."<<i+1<<"\t"<<minWalkLayer<<"Fs"<<endl;
}
cout<<endl;
return;
}
void StopAtOnlyOneFloor_FewestWalkLayer(int *_iFloorPassengerNum,int N)
{
int NBottom=0, NFloor=_iFloorPassengerNum[0], NAbove=0,minWalkLayer=0;
for(int i=1;i<N;++i)
{
NAbove+=_iFloorPassengerNum[i];
minWalkLayer=minWalkLayer+(_iFloorPassengerNum[i]*i);
}
int j=1;
for (;j<N;++j)
{
if(NAbove<NFloor+NBottom)break;
NAbove=NAbove-_iFloorPassengerNum[j];
NBottom=NBottom+NFloor;
NFloor=_iFloorPassengerNum[j];
minWalkLayer=minWalkLayer-NAbove-NFloor+NBottom;
}
cout<<"Best Stop is: No."<<j<<"F, at least Walks "<<minWalkLayer<<"Fs "<<endl;
return;
}
int main ()
{
int iFloorPassengerNum[FLOORSNUM];
cout<<"input the passengerNumbers for every floor:"<<endl;
for(int i=0;i<FLOORSNUM;i++)
{
cout<<"No."<<i+1<<": ";
cin>>iFloorPassengerNum[i];
}
StopAtOnlyOneFloor_AllFloorWalkLayers(iFloorPassengerNum,FLOORSNUM);
StopAtOnlyOneFloor_FewestWalkLayer(iFloorPassengerNum,FLOORSNUM);
return(0);
}
运行截图:
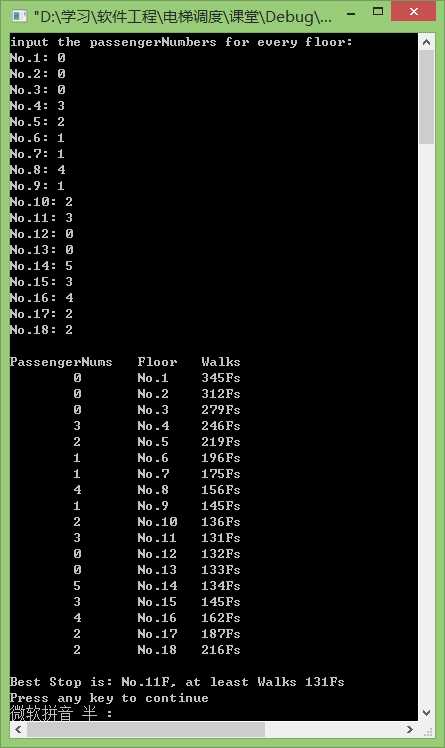
总结:
思路很难想到,因为一直在钻牛角尖,认为这道题目就是不对的,放到实际情况里根本不可行,还考虑了一大堆特殊的情况,类似什么半途有上人……但实际上老师更侧重的是想考察我们的思路,希望能在现有的思维方式上进行开拓。不管怎么样感觉实现起来也不容易。反正1~18层自己验算不快,在计算机上运行也还行,但从算法本身来看时间复杂度是O(n²),是很慢了。之间在关于求一维或者二维数组中最大子数组之和是就提示要考虑,可以看出时、空的复杂度在解决问题,特别是实现时是很重要的。
标签:
原文地址:http://www.cnblogs.com/mumulucky/p/4438889.html