Stat2—主成分分析（Principal components analysis）

标签：

最近在猛撸<R in nutshell>这本课，统计部分涉及的第一个分析数据的方法便是PCA！因此，今天打算好好梳理一下，涉及主城分析法的理论以及R实现！come on…gogogo…

首先说一个题外话，记得TED上有一期，一个叫Simon Sinek的年轻人提出了一个全新的Why-How-What黄金圈理论（三个同心圆，最里面的一个是Why,中间一层是How,最外面一层是What；一般人的思维习惯是从里面的圆逐渐推到外面，而创造了伟大作品、引领了伟大运动的人们，其思维习惯则恰恰相反，逆向思维的真相在于：要想最大程度影响他人，最关键的不在于传递“是什么”的信息，而在于给出“为什么”的理由），借由Apple这些年的成功告诉我们：消费者的消费文化已经变啦！企业要紧跟并迎合消费者思维的变化。一般来说，传统制造企业的逻辑思维是：我生产什么，我就卖什么？而现在的很多企业其实已经觉察到一个问题：就是企业要认清自己的地位，要客观而不是主观臆断，在当今这个瞬息万变（连我钟爱的诺基亚都消失于尘埃）的世界，企业要思辨，这根本在于人要思辨！在一个移动互联网的时代，企业和个人都要用互联网思维武装自己！而Simon Sinek所讲的即为互联网思维的一种体现。而学习一个新概念/技术的思路正好相反（正向思维）：what--->How--->why！这才是正常人的学习思维逻辑过程！以PCA这个新技术为例…

####所谓的“WHAT ”，就是搞清楚PCA是什么？有什么用？有什么语法（数据逻辑之类的）？有什么功能特性？有哪些应用领域？

####所谓的“HOW ”，就是搞清楚PCA内部是如何运作的？实现机制如何？等一系列相关问题。

####所谓的“WHY ”，就是搞清楚PCA为什么是这样的？为什么不是另外的样子？这样的设计有什么讲究？这就需要深刻理解PCA的内部逻辑以及与其他方法的差异(包括SW(即优势、劣势))

鉴于此，下面的关于PCA的介绍也围绕着这个逻辑来进行…

Step1：What  

主要回答：什么是PCA?有什么用/功能/特点？有什么语法(即背后的数学推理逻辑等)？

一. 问题引入

真实的训练数据总是存在各种各样的问题：

1、 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。

2、 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？

3、 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征->房价的这么多特征，就会造成过度拟合。

4、 这个与第二个有点类似，假设在IR中我们建立的文档-词项矩阵中，有两个词项为“learn”和“study”，在传统的向量空间模型中，认为两者独立。然而从语义的角度来讲，两者是相似的，而且两者出现频率也类似，是不是可以合成为一个特征呢？

5、 在信号传输过程中，由于信道不是理想的，信道另一端收到的信号会有噪音扰动，那么怎么滤去这些噪音呢？

下面探讨一种称作主成分分析（PCA）的方法来解决部分上述问题。PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主元，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

二. PCA的概念

R in nutshell一书的解释：Principal components analysis breaks a set of (possibly correlated) variables into a set of uncorrelated variables。

百科百科的解释：在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息！

wikipedia的解释：Principal component analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelatedvariables called principal components. The number of principal components is less than or equal to the number of original variables. This transformation is defined in such a way that the first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible), and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to (i.e., uncorrelated with) the preceding components. The principal components are orthogonal because they are the eigenvectorsof the covariance matrix, which is symmetric. PCA is sensitive to the relative scaling of the original variables。

我的理解：对比之后，发现还是维基百科的解释比较全面！可以简化为：主成分分析是将多指标化为少数几个综合指标的一种统计分析方法，是一种通过降维技术把多个变量化成少数几个主成分的方法，这些主成分能够反映原始变量的大部分信息，他们通常表示为原始变量的线性组合。其实，PCA本质特点是：压缩数据降维(此外还有因子分析 典型相关分析，这会在其他文章中介绍！)，以综合指标替代原数据进行分析！具体地说，为充分反映被研究对象个体之间的差异，人们会测量尽可能多的指标，以准确分类，但是指标的"多"增加了问题的复杂性。因此，能否压缩指标个数，以充分准确反映个体差异就成了PCA要解决的问题！三. PCA计算过程

# 首先介绍PCA的计算过程，假设我们得到的2维数据如下：

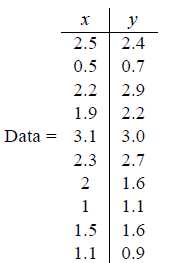@行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，x是千米/小时的速度，y是英里/小时的速度，等等。

第一步分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到：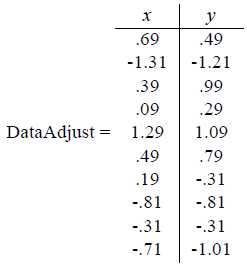

第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是：

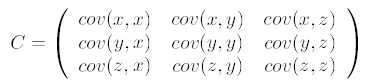这里只有x和y，求解得：

备注：对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

第三步，求协方差的特征值和特征向量（读者自己想一想为什么要计算特征值和特征向量？），得到：

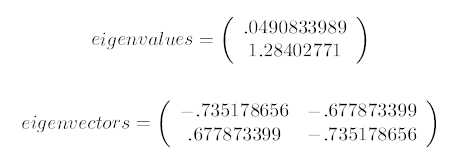备注：上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为，这里的特征向量都归一化为单位向量。

第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是

第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

这里是

FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量

得到结果是

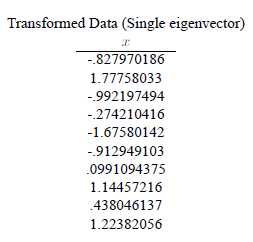
###这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。

上述过程有个图描述：

正号表示预处理后的样本点，斜着的两条线就分别是正交的特征向量（由于协方差矩阵是对称的，因此其特征向量正交），最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。

如果取的k=2，那么结果是：

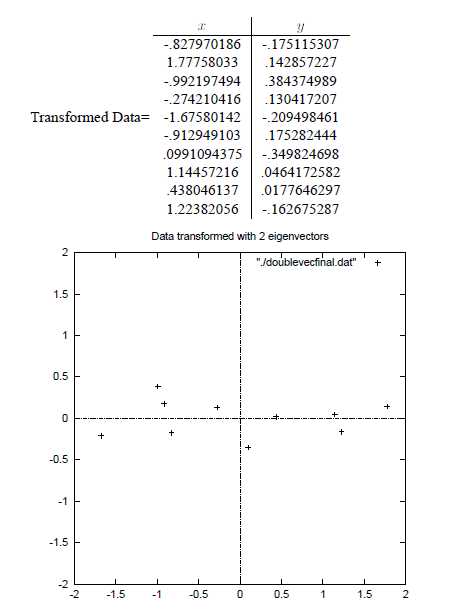
这样PCA的过程基本结束。在第一步减均值之后，其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度（0到100），一个是汽车的座位数（2到6），显然第二个的方差比第一个小。因此，如果样本特征中存在这种情况，那么在第一步之后，求每个特征的标准差，然后对每个样例在该特征下的数据除以。

归纳一下，使用我们之前熟悉的表示方法，在求协方差之前的步骤是：

其中是样例，共m个，每个样例n个特征，也就是说是n维向量。是第i个样例的第j个特征。是样例均值。是第j个特征的标准差。

整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。但是有没有觉得很神奇，为什么求协方差的特征向量就是最理想的k维向量？其背后隐藏的意义是什么？整个PCA的意义是什么

四. PCA的数据模型

对于一个样本资料，观测p 个变量（即特征）x₁, x₂ ,……,x_p， n 个样品（观测）的数据资料阵为：

主成分分析就是将p 个观测变量综合成为p 个新的变量（综合变量），即：

要求模型满足以下条件：

于是，称F₁为第一主成分，F₂ 为第二主成分，依此类推，有第p 个主成分。主成分又叫主分量。这里a_ij我们称为主成分系数。

五.PCA的几何解释

假设有n 个样品，每个样品有二个变量，即在二维空间中讨论主成分的几何意义。设n个样品在二维空间中的分布大致为一个椭园，如下图所示：

               @ 主成分几何解释图@

将坐标系进行正交旋转一个角度theta，使其椭圆长轴方向取坐标y1，在椭圆短轴方向取坐标y2，旋转公式为

经过旋转变换后，得到下图的新坐标：

新坐标y1—y2 有如下性质：
(1) n 个点的坐标y1和y2 的相关几乎为零。
(2)二维平面上的n 个点的方差大部分都归结为y1 轴上，而y2轴上的方差较小。
y1 和y2 称为原始变量x1 和x2的综合变量。由于n 个点在y1 轴上的方差最大，因而将二维空间的点用在y1 轴上的一维综合变量来代替，所损失的信息量最小，由此称y1 轴为第一主成分，y2 轴与y2 轴正交，有较小的方差，称它为第二主成分。

六.主成分的导出与主成分分析的步骤

1）主成分的导出

根据主成分分析的数学模型的定义，要进行主成分分析，就需要根据原始数据，以及模型的三个条件的要求，如何求出主成分系数，以便得到主成分模型。这就是导出主成分所要解决的问题。

1、根据主成分数学模型的条件①要求主成分之间互不相关，为此主成分之间的协差阵应该是一个对角阵（对角线上有值,其他地方均为0）。即，对于主成分：

F=AX

其协差阵应为：

2、设原始数据的协方差阵为V ，如果原始数据进行了标准化处理后则协方差阵等于相关矩阵，即有：

3、再由主成分数学模型条件③和正交矩阵的性质，若能够满足条件③最好要求A 为正交矩阵，即满足：

于是，将原始数据的协方差代入主成分的协差阵公式得：

展开上式得：

展开等式两边，根据矩阵相等的性质，这里只根据第一列得出的方程为：

为了得到该齐次方程的解，要求其系数矩阵行列式为0，即：

显然，是相关系数矩阵的特征值，是相应的特征向量。根据第二列、第三列等可以得到类似的方程，于是是方程

的p 个根为特征方程的特征根，是其特征向量的分量。

4、下面再证明主成分的方差是依次递减。

设相关系数矩阵R 的p 个特征根为，相应的特征向量为a_j

相对于F₁ 的方差为：

同样有：，即主成分的方差依次递减。并且协方差为：

综上所述，根据证明有，主成分分析中的主成分协方差应该是对角矩阵，其对角线上的元素恰好是原始数据相关矩阵的特征值，而主成分系数矩阵A 的元素则是原始数据相关矩阵特征值相应的特征向量。矩阵A 是一个正交矩阵。

于是，变量经过变换后得到新的综合变量：

新的随机变量彼此不相关，且方差依次递减。

2）主成分分析的计算步骤

样本观测数据矩阵为：

第一步：对原始数据进行标准化处理。

第二步：计算样本相关系数矩阵。

为方便，假定原始数据标准化后仍用X 表示，则经标准化处理后的数据的相关系数为：

第三步：用雅克比方法求相关系数矩阵R 的特征值和相应的特征向量

第四步：选择重要的主成分，并写出主成分表达式

主成分分析可以得到p 个主成分，但是，由于各个主成分的方差是递减的，包含的信息量也是递减的，所以实际分析时，一般不是选取p 个主成分，而是根据各个主成分累计贡献率的大小选取前k 个主成分，这里贡献率就是指某个主成分的方差占全部方差的比重，实际也就是某个特征值占全部特征值合计的比重。即：

贡献率越大，说明该主成分所包含的原始变量的信息越强。主成分个数k 的选取，主要根据主成分的累积贡献率来决定，即一般要求累计贡献率达到85%以上，这样才能保证综合变量能包括原始变量的绝大多数信息。

Step2：How

本节主要用R语言结合一个小案例来实战解析主成分分析的运用及结果分析。

一. 函数总结

#R中作为主成分分析最主要的函数是princomp()函数
#princomp()主成分分析  可以从相关阵或者从协方差阵做主成分分析
#summary()提取主成分信息 
#loadings()显示主成分分析或因子分析中载荷的内容
#predict()预测主成分的值 
#screeplot()画出主成分的碎石图 
#biplot()画出数据关于主成分的散点图和原坐标在主成分下的方向

二. 案例1

#现有30名中学生身高、体重、胸围、坐高数据，对身体的四项指标数据做主成分分析。

#1）载入原始数据

test<-data.frame(
X1=c(148, 139, 160, 149, 159, 142, 153, 150, 151, 139,140, 161, 158, 140, 137, 152, 149, 145, 160, 156,151, 147, 157, 147, 157, 151, 144, 141, 139, 148),
X2=c(41, 34, 49, 36, 45, 31, 43, 43, 42, 31,29, 47, 49, 33, 31, 35, 47, 35, 47, 44,42, 38, 39, 30, 48, 36, 36, 30, 32, 38),
X3=c(72, 71, 77, 67, 80, 66, 76, 77, 77, 68,64, 78, 78, 67, 66, 73, 82, 70, 74, 78,73, 73, 68, 65, 80, 74, 68, 67, 68, 70),
X4=c(78, 76, 86, 79, 86, 76, 83, 79, 80, 74,74, 84, 83, 77, 73, 79, 79, 77, 87, 85,82, 78, 80, 75, 88, 80, 76, 76, 73, 78)
)

> test
    X1 X2 X3 X4
1  148 41 72 78
2  139 34 71 76
3  160 49 77 86
4  149 36 67 79
5  159 45 80 86
6  142 31 66 76
7  153 43 76 83
8  150 43 77 79
9  151 42 77 80
10 139 31 68 74
11 140 29 64 74
12 161 47 78 84
13 158 49 78 83
14 140 33 67 77
15 137 31 66 73
16 152 35 73 79
17 149 47 82 79
18 145 35 70 77
19 160 47 74 87
20 156 44 78 85
21 151 42 73 82
22 147 38 73 78
23 157 39 68 80
24 147 30 65 75
25 157 48 80 88
26 151 36 74 80
27 144 36 68 76
28 141 30 67 76
29 139 32 68 73
30 148 38 70 78

#2）作主成分分析并显示分析结果

test.pr<-princomp(test,cor=TRUE)  #cor是逻辑变量 当cor=TRUE表示用样本的相关矩阵R做主成分分析；

                                                                                 当cor=FALSE表示用样本的协方差阵S做主成分分析

summary(test.pr,loadings=TRUE)  #loading是逻辑变量 当loading=TRUE时表示显示loading 的内容

                                                       #loadings的输出结果为载荷 是主成分对应于原始变量的系数即Q矩阵

> test.pr<-princomp(test,cor=TRUE)
> summary(test.pr,loadings=TRUE)
Importance of components:
                          Comp.1     Comp.2     Comp.3     Comp.4
Standard deviation     1.8817805 0.55980636 0.28179594 0.25711844
Proportion of Variance 0.8852745 0.07834579 0.01985224 0.01652747
Cumulative Proportion  0.8852745 0.96362029 0.98347253 1.00000000

Loadings:
   Comp.1 Comp.2 Comp.3 Comp.4
X1  0.497  0.543 -0.450  0.506
X2  0.515 -0.210 -0.462 -0.691
X3  0.481 -0.725  0.175  0.461
X4  0.507  0.368  0.744 -0.232

#3）分析结果含义
#----Standard deviation 标准差  其平方为方差=特征值
#----Proportion of Variance  方差贡献率
#----Cumulative Proportion  方差累计贡献率

#由结果显示 前两个主成分的累计贡献率已经达到96% 可以舍去另外两个主成分 达到降维的目的

因此可以得到函数表达式：

Z1=-0.497X‘1-0.515X‘2-0.481X‘3-0.507X‘4

Z1=  0.543X‘1-0.210X‘2-0.725X‘3-0.368X‘4

#4）画主成分的碎石图并预测

screeplot(test.pr,type="lines")

由碎石图可以看出 第二个主成分之后 图线变化趋于平稳 因此可以选择前两个主成分做分析！

> p<-predict(test.pr)
> p
           Comp.1      Comp.2      Comp.3       Comp.4
 [1,] -0.06990950 -0.23813701 -0.35509248 -0.266120139
 [2,] -1.59526340 -0.71847399  0.32813232 -0.118056646
 [3,]  2.84793151  0.38956679 -0.09731731 -0.279482487
 [4,] -0.75996988  0.80604335 -0.04945722 -0.162949298
 [5,]  2.73966777  0.01718087  0.36012615  0.358653044
 [6,] -2.10583168  0.32284393  0.18600422 -0.036456084
 [7,]  1.42105591 -0.06053165  0.21093321 -0.044223092
 [8,]  0.82583977 -0.78102576 -0.27557798  0.057288572
 [9,]  0.93464402 -0.58469242 -0.08814136  0.181037746
[10,] -2.36463820 -0.36532199  0.08840476  0.045520127
[11,] -2.83741916  0.34875841  0.03310423 -0.031146930
[12,]  2.60851224  0.21278728 -0.33398037  0.210157574
[13,]  2.44253342 -0.16769496 -0.46918095 -0.162987830
[14,] -1.86630669  0.05021384  0.37720280 -0.358821916
[15,] -2.81347421 -0.31790107 -0.03291329 -0.222035112
[16,] -0.06392983  0.20718448  0.04334340  0.703533624
[17,]  1.55561022 -1.70439674 -0.33126406  0.007551879
[18,] -1.07392251 -0.06763418  0.02283648  0.048606680
[19,]  2.52174212  0.97274301  0.12164633 -0.390667991
[20,]  2.14072377  0.02217881  0.37410972  0.129548960
[21,]  0.79624422  0.16307887  0.12781270 -0.294140762
[22,] -0.28708321 -0.35744666 -0.03962116  0.080991989
[23,]  0.25151075  1.25555188 -0.55617325  0.109068939
[24,] -2.05706032  0.78894494 -0.26552109  0.388088643
[25,]  3.08596855 -0.05775318  0.62110421 -0.218939612
[26,]  0.16367555  0.04317932  0.24481850  0.560248997
[27,] -1.37265053  0.02220972 -0.23378320 -0.257399715
[28,] -2.16097778  0.13733233  0.35589739  0.093123683
[29,] -2.40434827 -0.48613137 -0.16154441 -0.007914021
[30,] -0.50287468  0.14734317 -0.20590831 -0.122078819

三. 案例2：变量分类问题

#案例：已知16项指标的相关矩阵 从相关矩阵R出发 进行主成分分析  对16个指标进行分类

#1）载入相关系数 下三角表示（输入R之后，其实是以向量存储的）
x<-c(1.00,
0.79, 1.00,
0.36, 0.31, 1.00,
0.96, 0.74, 0.38, 1.00,
0.89, 0.58, 0.31, 0.90, 1.00,
0.79, 0.58, 0.30, 0.78, 0.79, 1.00,
0.76, 0.55, 0.35, 0.75, 0.74, 0.73, 1.00,
0.26, 0.19, 0.58, 0.25, 0.25, 0.18, 0.24, 1.00,
0.21, 0.07, 0.28, 0.20, 0.18, 0.18, 0.29,-0.04, 1.00,
0.26, 0.16, 0.33, 0.22, 0.23, 0.23, 0.25, 0.49,-0.34, 1.00,
0.07, 0.21, 0.38, 0.08,-0.02, 0.00, 0.10, 0.44,-0.16, 0.23, 1.00,
0.52, 0.41, 0.35, 0.53, 0.48, 0.38, 0.44, 0.30,-0.05, 0.50,0.24, 1.00,
0.77, 0.47, 0.41, 0.79, 0.79, 0.69, 0.67, 0.32, 0.23, 0.31,0.10, 0.62, 1.00,
0.25, 0.17, 0.64, 0.27, 0.27, 0.14, 0.16, 0.51, 0.21, 0.15,0.31, 0.17, 0.26, 1.00,
0.51, 0.35, 0.58, 0.57, 0.51, 0.26, 0.38, 0.51, 0.15, 0.29,0.28, 0.41, 0.50, 0.63, 1.00,
0.21, 0.16, 0.51, 0.26, 0.23, 0.00, 0.12, 0.38, 0.18, 0.14,0.31, 0.18, 0.24, 0.50, 0.65, 1.00)
)

> x

#2）输入16个指标的名称
names<-c("X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8","X9","X10", "X11", "X12", "X13", "X14", "X15", "X16")

#3）将矩阵生成相关矩阵 即原始下三角矩阵的扩展

R<-matrix(0,nrow=16,ncol=16,dimnames=list(names,names))

<-for(i in 1:16){
for(j in 1:i){
R[i,j]<-x[(i-1)*i / 2+j]; R[j,i]<-R[i,j] #这个公式略屌，有木有！

} }

> R
          X1   X2   X3   X4    X5    X6   X7     X8     X9    X10    X11   X12  X13  X14  X15  X16
X1  1.00 0.79 0.36 0.96  0.89 0.79 0.76  0.26  0.21  0.26  0.07  0.52 0.77 0.25 0.51 0.21
X2  0.79 1.00 0.31 0.74  0.58 0.58 0.55  0.19  0.07  0.16  0.21  0.41 0.47 0.17 0.35 0.16
X3  0.36 0.31 1.00 0.38  0.31 0.30 0.35  0.58  0.28  0.33  0.38  0.35 0.41 0.64 0.58 0.51
X4  0.96 0.74 0.38 1.00  0.90 0.78 0.75  0.25  0.20  0.22  0.08  0.53 0.79 0.27 0.57 0.26
X5  0.89 0.58 0.31 0.90  1.00 0.79 0.74  0.25  0.18  0.23 -0.02  0.48 0.79 0.27 0.51 0.23
X6  0.79 0.58 0.30 0.78  0.79 1.00 0.73  0.18  0.18  0.23  0.00  0.38 0.69 0.14 0.26 0.00
X7  0.76 0.55 0.35 0.75  0.74 0.73 1.00  0.24  0.29  0.25  0.10  0.44 0.67 0.16 0.38 0.12
X8  0.26 0.19 0.58 0.25  0.25 0.18 0.24  1.00 -0.04  0.49  0.44  0.30 0.32 0.51 0.51 0.38
X9  0.21 0.07 0.28 0.20  0.18 0.18 0.29 -0.04  1.00 -0.34 -0.16 -0.05 0.23 0.21 0.15 0.18
X10 0.26 0.16 0.33 0.22  0.23 0.23 0.25  0.49 -0.34  1.00  0.23  0.50 0.31 0.15 0.29 0.14
X11 0.07 0.21 0.38 0.08 -0.02 0.00 0.10  0.44 -0.16  0.23  1.00  0.24 0.10 0.31 0.28 0.31
X12 0.52 0.41 0.35 0.53  0.48 0.38 0.44  0.30 -0.05  0.50  0.24  1.00 0.62 0.17 0.41 0.18
X13 0.77 0.47 0.41 0.79  0.79 0.69 0.67  0.32  0.23  0.31  0.10  0.62 1.00 0.26 0.50 0.24
X14 0.25 0.17 0.64 0.27  0.27 0.14 0.16  0.51  0.21  0.15  0.31  0.17 0.26 1.00 0.63 0.50
X15 0.51 0.35 0.58 0.57  0.51 0.26 0.38  0.51  0.15  0.29  0.28  0.41 0.50 0.63 1.00 0.65
X16 0.21 0.16 0.51 0.26  0.23 0.00 0.12  0.38  0.18  0.14  0.31  0.18 0.24 0.50 0.65 1.00

> x<-c(1,-1,1,-2,-3,1)
> names<-c(‘x1‘,‘x2‘,‘x3‘)
> R<-matrix(0,nrow=3,ncol=3,dimnames=list(names,names))
> R
   x1 x2 x3
x1  0  0  0
x2  0  0  0
x3  0  0  0
> for(i in 1:3){
+     for(j in 1:i){
+         R[i,j]<-x[(i-1)*i/2+j];R[j,i]<-R[i,j] #可见该公式可将相关系数下三角转化成相关矩阵
+     }
+ }
> R
   x1 x2 x3
x1  1 -1 -2
x2 -1  1 -3
x3 -2 -3  1

#4）主成分分析

> x.pr<-princomp(covmat=R)  #covmat协方差阵（指定使用相关矩阵来进行PCA分析！）
> x.pr
Call:
princomp(covmat = R)
Standard deviations:
Comp.1    Comp.2    Comp.3    Comp.4    Comp.5    Comp.6    Comp.7    Comp.8    Comp.9   Comp.10   Comp.11   Comp.12   Comp.13   Comp.14   Comp.15   Comp.16 
2.6526359 1.6167971 1.2775386 0.9217124 0.8763498 0.8037803 0.6873924 0.6753023 0.5975465 0.5559751 0.4901757 0.4666029 0.4112178 0.3675549 0.2607323 0.1699982
16  variables and  NA observations.
> load<-loadings(x.pr)  #载荷

#5）散点图
plot(load[,1:2])   #取前两个主成分,画两个主成分的散点图！
text(load[,1],load[,2],adj=c(-0.4,0.3))、

通过散点图可以得到分析结果：指标1 2 4 5  6 7 13可以归为一类 ；指标9 10 12可以归为一类；指标3 8 11 14 15 16可以归为一类。

本节附录

四. 案例3：主成分回归问题（后面再补充！）

#考虑进口总额Y与三个自变量：国内总产值，存储量，总消费量之间的关系。现收集了1949-1959共11年的数据，试做线性回归和主成分回归分析。
economy<-data.frame(
x1=c(149.3, 161.2, 171.5, 175.5, 180.8, 190.7, 202.1, 212.4, 226.1, 231.9, 239.0),
x2=c(4.2, 4.1, 3.1, 3.1, 1.1, 2.2, 2.1, 5.6, 5.0, 5.1, 0.7),
x3=c(108.1, 114.8, 123.2, 126.9, 132.1, 137.7, 146.0, 154.1, 162.3, 164.3, 167.6),
y=c(15.9, 16.4, 19.0, 19.1, 18.8, 20.4, 22.7, 26.5, 28.1, 27.6, 26.3)
)

> economy
      x1  x2    x3    y
1  149.3 4.2 108.1 15.9
2  161.2 4.1 114.8 16.4
3  171.5 3.1 123.2 19.0
4  175.5 3.1 126.9 19.1
5  180.8 1.1 132.1 18.8
6  190.7 2.2 137.7 20.4
7  202.1 2.1 146.0 22.7
8  212.4 5.6 154.1 26.5
9  226.1 5.0 162.3 28.1
10 231.9 5.1 164.3 27.6
11 239.0 0.7 167.6 26.3

#1）线性回归
lm.sol<-lm(y~x1+x2+x3, data=economy)
summary(lm.sol)

@结果

> lm.sol<-lm(y~x1+x2+x3, data=economy)
> summary(lm.sol)

Call:
lm(formula = y ~ x1 + x2 + x3, data = economy)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.52367 -0.38953  0.05424  0.22644  0.78313 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -10.12799    1.21216  -8.355  6.9e-05 ***
x1           -0.05140    0.07028  -0.731 0.488344    
x2            0.58695    0.09462   6.203 0.000444 ***
x3            0.28685    0.10221   2.807 0.026277 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4889 on 7 degrees of freedom
Multiple R-squared:  0.9919,	Adjusted R-squared:  0.9884 
F-statistic: 285.6 on 3 and 7 DF,  p-value: 1.112e-07

###2）主成分回归
# 主成分分析
conomy.pr<-princomp(~x1+x2+x3, data=economy, cor=T)
summary(economy.pr, loadings=TRUE)

Importance of components:
                         Comp.1    Comp.2       Comp.3
Standard deviation     1.413915 0.9990767 0.0518737839
Proportion of Variance 0.666385 0.3327181 0.0008969632
Cumulative Proportion  0.666385 0.9991030 1.0000000000

Loadings:
   Comp.1 Comp.2 Comp.3
x1 -0.706         0.707
x2        -0.999       
x3 -0.707        -0.707

pre<-predict(economy.pr)
economy$z1<-pre[,1]; economy$z2<-pre[,2]

> economy
      x1  x2    x3    y         z1          z2
1  149.3 4.2 108.1 15.9  2.2296493 -0.66983032
2  161.2 4.1 114.8 16.4  1.6979452 -0.58265445
3  171.5 3.1 123.2 19.0  1.1695976  0.07654175
4  175.5 3.1 126.9 19.1  0.9379462  0.08639036
5  180.8 1.1 132.1 18.8  0.6756511  1.37046303
6  190.7 2.2 137.7 20.4  0.1996423  0.69131968
7  202.1 2.1 146.0 22.7 -0.3771746  0.77997236
8  212.4 5.6 154.1 26.5 -1.0192344 -1.42014882
9  226.1 5.0 162.3 28.1 -1.6354243 -1.01109953
10 231.9 5.1 164.3 27.6 -1.8532401 -1.06476864
11 239.0 0.7 167.6 26.3 -2.0253583  1.74381457

Call:
lm(formula = y ~ z1 + z2, data = economy)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.89838 -0.26050  0.08435  0.35677  0.66863 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  21.8909     0.1658 132.006 1.21e-14 ***
z1           -2.9892     0.1173 -25.486 6.02e-09 ***
z2           -0.8288     0.1660  -4.993  0.00106 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.55 on 8 degrees of freedom
Multiple R-squared:  0.9883,	Adjusted R-squared:  0.9853 
F-statistic: 337.2 on 2 and 8 DF,  p-value: 1.888e-08

Stat2—主成分分析（Principal components analysis）

标签：

原文地址：http://www.cnblogs.com/Bfrican/p/4440486.html