标签:
梯度下降法存在的问题
梯度下降法的基本思想是函数沿着其梯度方向增加最快,反之,沿着其梯度反方向减小最快。在前面的线性回归和逻辑回归中,都采用了梯度下降法来求解。梯度下降的迭代公式为:
\(\begin{aligned} \theta_j=\theta_j-\alpha\frac{\partial\;J(\theta)}{\partial\theta_j} \end{aligned} \)
在回归算法的实验中,梯度下降的步长\(\alpha\)为0.01,当时也指出了该步长是通过多次时间找到的,且换一组数据后,算法可能不收敛。为什么会出现这样的问题呢?从梯度下降法的出发点可以看到,算法指出了行进的方向,但没有明确要行进多远,那么问题就来了,步子太小,走个一千一万年都到不了终点,而步子太大,扯到蛋不说,还可能越跑越远。
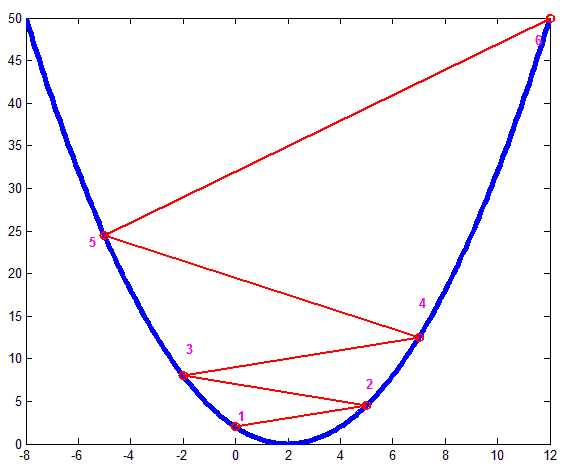
如上图,蓝色为一个碗形函数,其最小值在\(x=2\)那点,假如从\(x=0\)开始迭代,即是图中点1,此时知道应该向右走,但步子太大,直接到点2 了,同样点2处知道该往左走,结果又跑太远到点3了,…,这样越走越偏离我们的终点了。此情况的验证可以直接把前面回归算法的步长改大,比如把线性回归迭代步长改为10,要不了几次迭代结果就是Nan了。
这样有一点需要说明下,同样的步长\(\alpha\),为何从1到2和2到3的长度不一致?因为1-6点的梯度是逐步增大的,故虽然步长相同,但移动的距离却越来越远,从而进入了一个恶性循环了。
解决方法
对于上面提出的问题,解决方法有多种,下面就大致来说说,若有新的方法此处未提及,欢迎补充。
1.手动测试法
顾名思义,此方法需要手动进行多次实验,不停调整参数,观测实验效果,最终来确定出一个最优的步长。那么如何判断实验效果的好坏呢?一种常用的方法是观察代价函数(对线性回归而言)的变化趋势,如果迭代结束后,代价函数还在不停减少,则说明步长过小;若代价函数呈现出振荡现象,则说明步长过大。如此多次调整可得到较合理的步长值。
显然,该方法给出的步长对于这组训练样本而言是相对较优的,但换一组样本,则需要重新实验来调整参数了;另外,该方法可能会比较累人~~
2.固定步进
这是一个非常保险的方法,但需要舍弃较多的时间资源。既然梯度下降法只给出方向,那么我们就沿着这个方向走固定路程,即将梯度下降迭代公式修改为:
\(\begin{aligned} \theta_j=\theta_j-\alpha\;sign({\frac{\partial\;J(\theta)}{\partial\theta_j}}) \end{aligned} \)
其中的\(sign\)是符号函数。
那么\(\alpha\)取多大呢?就取可容许的最小误差,这样的迭代方式可以保证必然不会跨过最终点,但需要耗费更多次迭代。
3.步长衰减
步长衰减主要考虑到越接近终点,每一步越需要谨慎,故把步长减小,宁肯多走几步也绝不踏错一步。在吴恩达公开课中,他也提到了可在迭代中逐步减少步长。那如何减少步长?通常可以有这么几种做法:
A.固定衰减。比如每次迭代后,步长衰减为前一次的某个比例(如95%)。
B.选择性衰减。根据迭代状态来确定本次是否衰减,可以根据梯度或代价函数的情况来确定。比如,若此次迭代后代价函数增加了,则说明上次迭代步长过大,需要减小步长,否则保持不变,这么做的一个缺点是需要不停计算代价函数,训练样本过多可能会大大增加耗时;也可以根据梯度变化情况来判断,我们知道我们的终点是梯度为0的地方,若本次迭代后的梯度与前一次的梯度方向相反,则说明跨过了终点,需要减小步长。
显然,采用步长衰减的方式,同样也依赖于初始步长,否则可能不收敛。当然其相对于固定步长,则会更具稳定性。
4.自适应步长
此方法思想来源与步长衰减。在每次迭代,按照下面步骤来计算步长:
A.设置一个较大的初始步长值
B.计算若以此步长移动后的梯度
C.判断移动前后梯度方向是否会改变,若有改变,将步长减半,再进行A步;否则,以此步长为本次迭代的步长。
还是以上面那个图像来说明下。首先,初始点1在\(x=0\)处,按照初始步长则应该移动到点2\(x=5\)处,可点1和2处梯度方向改变了,那边步长减半则应该到点A\(x=2.5\)处,点1与A的梯度还是不同,那再将步长减半,则移动到点B\(x=1.25\)处,由于点1与B的梯度方向相同,则此次迭代将从1移动到B。
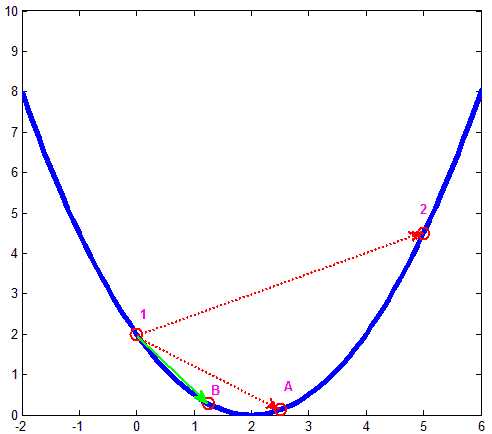
显然,该方法不会收到初始步长的影响,每次自动计算使得不会跨过终点的最大步长值。另一方面,从计算量上讲,有可能会比原来的方式更大,毕竟有得有失,你不用自己去一次次修改参数->运行程序->观察结果->…->修改参数。具体代码只需对原回归算法的代码略做修改即可。
将原回归算法迭代中的2行代码
1 Grad = CalcGrad(TX, TY, Theta, fun); 2 Theta = Theta + Alpha .* Grad;
修改为

1 Alpha = 16 * ones(n, 1); 2 Theta0 = Theta; 3 Grad0 = CalcGrad(TX, TY, Theta0, fun); 4 while(min(Alpha) > eps) 5 Theta1 = Theta0 + Alpha .* Grad0; 6 Grad1 = CalcGrad(TX, TY, Theta1, fun); 7 s = sign(Grad1 .* Grad0); 8 if (min(s)>=0) 9 break; 10 end 11 12 s(s==-1) = 0.5; 13 s(s==0) = 1; 14 Alpha = Alpha .* s; 15 end 16 Grad = Grad0; 17 Theta=Theta1;
即可实现。
补充说明
上面的说明是针对每一维的,对于步长需要每一维计算。若需要所有维度使用同一个步长,请先将训练样本归一化,否则很可能收敛不到你想要的结果。
标签:
原文地址:http://www.cnblogs.com/jcchen1987/p/4441743.html