标签:
石家庄铁道大学基础教学楼一共有四部电梯,每层都有人上下,电梯在每一层都停。信1201-1班张一东每层都停有点儿不耐烦。如果在上下课高峰时刻电梯从一层上行,但只允许停留在某一层。每个人选择自己的目的地,使他们爬楼层数最少。
1,(基础算法)首先用最笨的办法去思考这个问题,就是让电梯从第二层楼开始停。然后计算所有人爬楼层数之和,知道第N层,然后找出爬楼层数最少的就是电梯要停留的层数。
2,(优化算法)假设电梯停在第 i 层楼,我们计算出所有乘客总共爬楼梯的层数是Y。如果有N1个乘客想去的楼层在第 i 层之下,有N2个乘客正好想去的楼层是第 i 层,有N3个乘客想去的楼层在第 i 层之上。这个时候,重点来了:如果电梯改停在i-1层,所有目的地在第i - 1层以下的乘客可以少爬1层,总共少爬N1层,所有在i层及以上的乘客要多爬一层,总共多爬N2+N3层,这时总共需要爬Y-N1+N2+N3。反之,如果电梯在i+1层停所有目的地在第 i 层以上的乘客可以少爬1层,总共少爬N3层,所有在 i 层及以下的乘客要多爬一层,总共多N1+N2层,这时总共需要爬Y+N1+N2-N3层。可见,当N1 > N2+N3 时,电梯在第i-1层楼停更好;当N1+N2 < N3 时,电梯在i+1层停更好。其他情况在第i层更好。如此一来,问题的解法就出来了,从第一层开始考察,计算各位乘客走的楼层的数目,然后根据N1,N2,N3之间的关系进行调整,知道找到最佳楼层。
package com.java.com.aikan;
import java.util.Scanner;
public class dianti2 {
public static void main(String[] args){
int N,num;//电梯层数,乘客要停的电梯数
Scanner in=new Scanner(System.in);
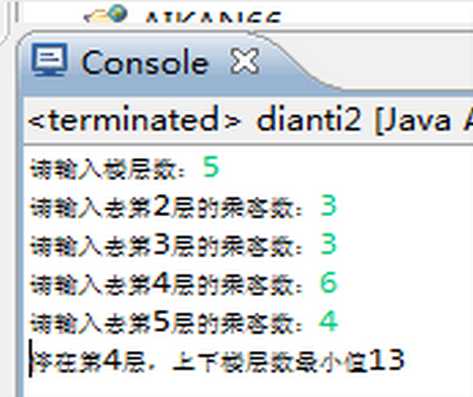
System.out.print("请输入楼层数:");
N=in.nextInt();
int array[]=new int[N+1];
for(int i=2;i<=N;i++)
{
System.out.print("请输入去第"+i+"层的乘客数:");
array[i]=in.nextInt();
}
youhua(N,array);
}
}
public static void youhua(int N,int array[])//优化
{
int N1=0,N2=0,N3=0,i,j,k;
int min=0,m=2,sum=0;
array[1]=0;
for(i=2;i<=N;i++)
sum+=array[i];
for(i=2;i<=N;)
{
N1+=array[i-1];
N2=array[i];
N3=sum-N1-N2;
if(N1+N2<N3)
i++;
else
break;
}
for(j=2;j<=N;j++)
{
k=i>j?(i-j):(j-i);
min+=array[j]*k;
}
System.out.println("停在第"+i+"层,上下楼层数最小值"+min);
}
}
我们两个人没有想到什么优化方案,只是想到了最本的方法,经过老师的讲解,还是没有能够理解,最后又跟其他小队商量大概理解了算法思想。两个人如果不行还是要求助同学。
标签:
原文地址:http://www.cnblogs.com/zhaixing/p/4442371.html