标签:
思路:
(1)暴力穷举。O(n^3) -----绝对不行。
穷举所有可能的出现子串O(n^2),再判断是否回文O(n)。就是O(n*n*n)了。
(2)记录位置。O(n^3) -----绝对不行。
先扫一遍,记录每个字符在上一次出现的位置pos。每次考虑第i个字符,如果回文子串包括 i 的话,那么肯定在i的前面有一个跟第i个字符是一样的,利用之前记录的位置pos[i]可以找到与第i个相同的字符,如果i-pos[i]比之前发现的最长的子串max还短,那么不用比较了。如果更前面还有和第i个字符一样的,那么可以找到第pos[pos[i]]个,一定要找到区间比max还大的,才有比较的意义,除非前面已经没有相同字符的了。那么略过第i个,直奔下一个。记录位置需要O(n),考虑每个字符需要O(n),对其前面出现过的每个字符考虑O(n),一旦考虑就需要比较是否回文O(n),总的来说,后面3个是乘的关系O(n^3)。

1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 #include <stdio.h> 5 6 using namespace std; 7 const int N=1000010; 8 9 char str[N]; 10 char has[256]; 11 char pos[N]; 12 13 14 bool isP(int j,int i) 15 { 16 while( j!=i && j!=--i) 17 { 18 if( str[j]!=str[i] ) 19 return false; 20 j++; 21 } 22 return true; 23 } 24 25 int fin_ex(int max, int i) 26 { 27 int j=pos[i]; 28 while( i-j<=max && j>-1 ) //找到一个区间范围大于max的,开始算 29 j=pos[j]; 30 return j; 31 } 32 33 int cal(int len) 34 { 35 int max=1, j; 36 for(int i=0; i<len; i++) 37 { 38 j=fin_ex(max, i); //找相同的,且大于max的 39 while( j!=-1 && i-j>max ) //有相同 40 { 41 if(isP(j,i+1)==true) 42 max=i-j+1; 43 else 44 j=fin_ex(max, j); //不是回文,继续找 45 } 46 } 47 return max; 48 } 49 50 51 int main() 52 { 53 //freopen("input.txt", "r", stdin); 54 int t; 55 cin>>t; 56 getchar(); 57 while(t--) 58 { 59 gets(str); 60 int len=strlen(str); 61 for(int i=0; i<256; i++) has[i]=-1; //初始化 62 for(int i=0; i<len; i++) //记录上一次出现的位置 63 { 64 pos[i]=has[str[i]]; 65 has[str[i]]=i; 66 } 67 68 cout<<cal(len)<<endl; 69 } 70 return 0; 71 }
(3)动态规划。时间O(n^2),空间O(n^2)----这空间已经不行了。
不考虑了,这空间接受不了。
(4)中心扩展。时间O(n^2),空间O(0)。-----这时间已经不行了。
扫一遍每个字符需要O(n),对每个字符进行回文判断需要O(n)。总的就O(n^2)。

1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 #include <stdio.h> 5 6 using namespace std; 7 const int N=1000010; 8 int len; 9 char str[N]; 10 11 int isP(int i) //以i为中点的最长回文串的长度 12 { 13 int max1=1; 14 //奇数 15 int tmp=max(i,len-i-1); 16 17 for(int j=1; j<=tmp; j++) 18 { 19 if( str[i-j]==str[i+j] ) 20 max1+=2; 21 else 22 break; 23 } 24 25 //偶数 26 int max2=0; 27 tmp =max(i+1, len-i-1); 28 for(int j=0; j<tmp; j++) 29 { 30 if( str[i-j]==str[i+j+1] ) 31 max2+=2; 32 else 33 break; 34 } 35 return max1>max2? max1:max2; 36 } 37 38 int cal() 39 { 40 int max=1, tmp; 41 for(int i=1; i<len-1; i++) //考虑以i为中心的回文串 42 { 43 if( (tmp=isP(i))>max ) 44 max=tmp; 45 } 46 return max; 47 48 } 49 50 int main() 51 { 52 //freopen("input.txt", "r", stdin); 53 int t; 54 cin>>t; 55 while(t--) 56 { 57 scanf("%s",str); 58 len=strlen(str); 59 if(len==1){cout<<"1"<<endl;continue;} 60 cout<<cal()<<endl; 61 } 62 return 0; 63 }
(5)特殊处理。时间O(n),空间O(n)。------完全OK!
主要目的就是要减少计算量,在”中心扩展“法的基础上,节省更多的计算量。下面介绍这种处理方法。
步骤:
1)首先要插入一些奇怪的字符。作用是,使得每种可能出现的子串的长度变成永远是奇数。如 abba 变成 #a#b#b#a#。假设串长为n,那么其实是加入了n+1个#号,使得串长总是2*n+1,这样就必定是奇数了。而且在用”中心扩展“法时仍然是奇数,考虑奇数子串#b#,偶数子串b#b,如果中间是#号,那么计算的就是偶数的子串了。置s[0]=‘¥’,随便一个特殊的字符,可以省去计算时的判断的左边界,比对到这个¥特殊符号,肯定没有任何一个是跟他匹配的,最长匹配过程自动就被终止了。而右边界有‘\0‘,自然也没有任何符号会跟他匹配。
2)接着需要记录下每个字符的关于最长子串的一些“信息”,不是长度,而是一个可以计算出长度的数字,其实是(纯长度+1),为什么要这么做?这其实是个边界。即下面提到的mx,在i到mx之间的字符都可以节省一些计算量。
(mx的对称点,id)和(id,mx)是对称的,即回文。能使得mx越靠右的字符就作为id,所以得及时凭借mx大小来更新id和mx。在(id,mx)中任意一个点都会和id左边对称的字符一样,那么 i 的最小回文就跟 j 的最大回文有关了,这也是减少计算量的突破口。有下面两种情况,
(1)P[j]不会超过左边”mx的对称点“ 。那么这在P[id]管辖的范围内,有左右对称的原理,所以P[i]至少为P[j]吧,但是可能会更大,因为左边的是比较过的才求出P[j],这P[i]还没比较过,所以长度可以从P[j]开始比对了。这样就节省了这P[j]次比较了。
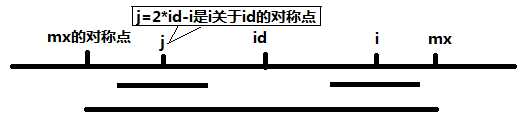
(2)P[j]超过了左边”mx的对称点“ 。超过了id的管辖范围了,多出的部分保证不了左右对称的原理了,但是在id管辖范围内的肯定是符合对称原理的,那么至少也可以减少一些计算量呐,减多少呢?就是”id管辖范围内“那个P[j]的长度了,做一些计算就可以得到这个长度是多少,但是肯定是小于P[j]的。
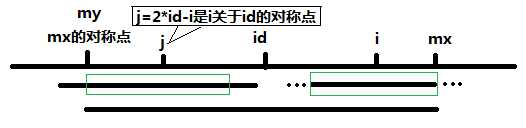
注:那如果i逐渐扫到mx之外了怎么办,i肯定找不到再关于id对称的j了。那就老老实实比较吧,继续用中心扩展。

1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 #include <stdio.h> 5 using namespace std; 6 const int N=1000010; 7 int len; //原串长 8 char str[N]; //接收原来的串 9 char s[N*2]; //做了插入处理的结果串 10 int P[N*2]; //保存关于长度的信息(回文长度的一半再加1) 11 int cal() 12 { 13 int id=1, mx=1, max1=1; 14 P[0]=1; 15 P[1]=1; 16 for(int i=2; s[i]!=‘\0‘; i++) //考虑以i为中心的回文串 17 { 18 P[i] =i>mx? 1: min( P[2*id-i],mx-i); 19 while(s[i+P[i]]==s[i-P[i]]) //在这比对 20 P[i]++; 21 if(i+P[i]>mx) //更新id和mx的位置 22 { 23 id=i; 24 mx=i+P[i]; 25 } 26 if(P[i]-1>max1) //更新最大值 27 max1=P[i]-1; 28 } 29 return max1; 30 } 31 32 int main() 33 { 34 freopen("input.txt", "r", stdin); 35 int t; 36 cin>>t; 37 while(t--) 38 { 39 scanf("%s",str); 40 len=strlen(str); 41 memset(s,0,sizeof(s)); 42 memset(P,0,sizeof(P)); 43 44 //插入符号# 45 s[0]=‘$‘; 46 s[1]=‘#‘; 47 int i=0, j=2; 48 for(; i<len; i++) 49 { 50 s[j++]=str[i]; 51 s[j++]=‘#‘; 52 } 53 cout<<cal()<<endl; 54 } 55 return 0; 56 }
hihoCoder hiho一下 第一周 #1032 : 最长回文子串 (特殊处理)
标签:
原文地址:http://www.cnblogs.com/xcw0754/p/4442652.html