标签:
本文不是原创, 转自这里, 只是对排版有所改进.
我们知道有$\textrm{rank}(AB)\leq \textrm{min}\{\textrm{rank} (A),\ \textrm{rank} (B)\}$$,$ 且若$A$或$B$可逆$,$ 不等号将变成等号$.$
所以对于任意方阵$A$和$k$有$\textrm{rank}(A^{k+1})\leq\textrm{rank}(A^k).$ 也就是说$\textrm{rank}(A^k)$是$k$的单调减函数.
但是这个函数有没有什麽更深刻的性质呢$?$
$\textbf{引理: }$$\textrm{rank}(ABC)+\textrm{rank} (B) \geq \textrm{rank}(AB)+\textrm{rank}(BC).$
$\textbf{证明: }$做初等变换$$\left( {\begin{array}{*{20}{c}}{ABC}&0\\ 0&B\end{array}} \right) \to \left( {\begin{array}{*{20}{c}}{ABC}&{AB}\\ 0&B\end{array}} \right) \to \left( {\begin{array}{*{20}{c}}0&{AB}\\ { - BC}&B\end{array}} \right) \to \left({\begin{array}{*{20}{c}}{AB}&0\\ B&{BC}\end{array}} \right).\ 得证.$$
$\textbf{推论: }$$\textrm{rank}(A^k)-\textrm{rank}(A^{k+1})\leq \textrm{rank}(A^{k-1})-\textrm{rank}(A^k).$
$\textbf{证明: }$将引理中的$B$换为$A^{k-1}$$,$ $C$换为$A$即可得证$.$
上述推论说明了$\textrm{rank}(A^k)$随$k$的增大而下降$,$ 且下降值也越来越小$.$
$\textbf{定理1: }$若存在$k$使得$\textrm{rank}(A^k)=\textrm{rank}(A^{k+1})$$,$ 则$\textrm{rank}(A^k)=\textrm{rank}(A^{k+1})=\textrm{rank}(A^{k+2})=\textrm{rank}(A^{k+3})=\cdots\cdots$
$\textbf{证明: }$利用推论以及$\textrm{rank}(A^k)$是$k$的单调减函数$,$ 得知$0\leq \textrm{rank}(A^{k+1})-\textrm{rank}(A^{k+2})\leq \textrm{rank}(A^k)-\textrm{rank}(A^{k+1})=0$$,$ 得证$.$
$\textbf{定理2: }$若$A$是$n$阶方阵$,$ 则$\textrm{rank}(A^n)=\textrm{rank}(A^{n+1})=\textrm{rank}(A^{n+2})=\textrm{rank}(A^{n+3})=\cdots\cdots$
$\textbf{证明: }$反证法$,$ 若$\textrm{rank}(A^n)>\textrm{rank}(A^{n+1})$$,$ 则说明秩降在$n$处没有停止$,$ 说明$i\leq n$时有$\textrm{rank}(A^i)\geq \textrm{rank}(A^{i+1})+1$$,$ 推出$\textrm{rank} (A)\geq \textrm{rank}(A^{n+1})+n$$.$ 因为$\textrm{rank} (A)>\textrm{rank}(A^2)$$,$ 说明$A$不可逆$,$ 所以$\textrm{rank} (A)\leq n-1$$.$ 因此得出$\textrm{rank}(A^{n+1})\leq -1$$,$ 不可能出现$.$ 所以得证$.$
以上定理说明了$\textrm{rank}(A^k)$是$k$的单调减函数$,$ 且下降值也越来越小$.$
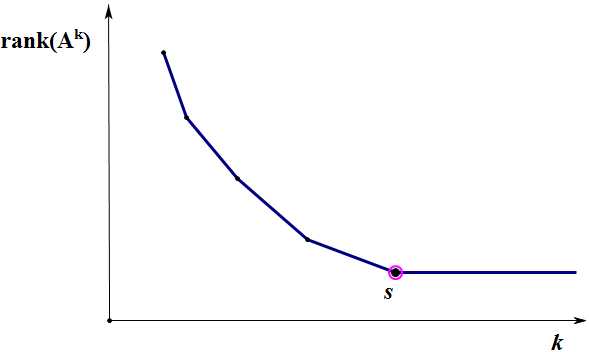
在某处停止以后就会保持不变$,$ 且停止秩降的点一定会在某个$s\leq n$处达到$.$
因此$,$ $\textrm{rank}(A^k)$和$k$的关系将会如下图所示$:$
标签:
原文地址:http://www.cnblogs.com/poorich/p/4446704.html