标签:
Monty Hall是上个世纪60年代,电视游戏节目“Let‘s Make a Deal”的主持人,这个悖论便是以他的名字来命名的。节目的规则是这样的:
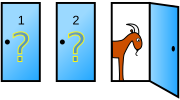
Monty向你展示三个关闭的大门,其中一扇门背后有一辆车,另两扇门背后是一头山羊。
 [1]
[1]
参与节目的观众会穿着奇装异服,希望Monty能够选中自己。
首先你可以任意选择一扇门,当然你有1/3的概率选中背后有车的门。
这时Monty会打开另一扇,他知道后面没有车(这是一个极其需要注意的细节),并询问你是否需要改变你的选择。
Monty知道那扇门背后有车,你认为他是设计让你没法得到车,还是在帮你呢?这时台下的观众也会乱作一团,各自嚷嚷着自己的猜想。
到底应该坚持自己最初的选择,还是改变自己的选择呢,如果你是在考试结束的前一分钟,我想你应当坚持自己的选择。
作为聪明的你,如果你一开始胡乱动用自己的情感,你就已经输了。要想得到正确的结论,必须依靠理性。
1 分析所有可能发生的情况
一开始,如果不知道开始从哪儿开始思考,不妨假设所有可能发生的情况。
不失一般性,假设车出现在1号门后
你选择了1号门,Monty会随机打开2号或3号门,这时应坚持自己的选择选择
你选择了2号门,1号门背后有车,Monty只能打开3号门,这是应该改变自己的选择
你选择了3号门,根选择2号门的情况完全相同
[2]
你看,1/3的情况坚持自己的选择能够得到车,2/3的情况改变自己的选择能够得到车
所以你应当改变自己的选择
2 使用随机变量分析
要使用概率论来分析,最重要的是明确随机变量是什么。你必须以第三者视角俯视这个问题,
车的位置一定是随机的,你的选择也是随机的,Monty的选择呢,有时他迫不得已只有一个选择,有时他有可以从两扇门里,随意选择一张,所以还是随机的
假设,随机变量X代表你的选择、随机变量Y代表Monty打开的门、随机变量Z代表真实车的位置
三个随机变量的取值,均为A、B或C,代表三扇门
还有,随机变量X与随机变量Z是相互独立的,因为你不知道车在哪
问题应当描述成,你选择了门A,Monty打开了门B,求车位于门C的概率,也就是改变选择得到车的概率。并没有失去一般性
得出的结果是,2/3的概率改变你的选择能够得到车
3 计算机仿真
如果你对概率没有兴趣,认为概率虚无缥缈,仍然有办法可以解救你,那就是计算机仿真。这里会使用Python编程语言,来模拟这一过程。
你只需要用三个随机数,模拟上一种方法说明的三个随机变量,然后统计坚持选择得到车和改变选择得到车的次数就能得到分布。
def montyChoose(guessDoor, prizeDoor):
if 1 != guessDoor and 1 != prizeDoor:
return 1
if 2 != guessDoor and 2 != prizeDoor:
return 2
return 3
此函数用于模拟Monty的选择,一个简单的逻辑就是,Monty只能选你没有选的门,同时又没有车的门
def simMontyHall(numTrials):
stickWins, switchWins, noWin = (0, 0, 0)
for t in range(numTrials): #进行numTrails次实验
prizeDoor = random.choice([1, 2, 3]) #随机生成车所在的门
guess = random.choice([1, 2, 3]) #随机生成你的选择
toOpen = montyChoose(guess, prizeDoor)
if toOpen == prizeDoor: #模拟Monty的选择 这种情况并不会发生
noWin += 1
elif guess == prizeDoor:
stickWins += 1
else:
switchWins += 1
return (stickWins, switchWins)
将函数返回的结果画成饼状图
得到的结果和上面仍然是一致的。
在最开始介绍节目的游戏规则时,我特意强调了,Monty知道车的位置很重要,Monty会避开选中车
如果Monty并不知道车在哪,随机打开一个门呢,这时他有可能自己打开背后有车的门,但并不会直接打开你选择的门
修改一下上面的选择函数为随机选择,就可以模拟这种新的情况
def randomChoose(guessDoor, prizeDoor):
if guessDoor == 1:
return random.choice([2,3])
if guessDoor == 2:
return random.choice([1,3])
return random.choice([1,2])
这样,不论你是否修改你的选择,并没有区别
全部代码:
import pylab
import random
def montyChoose(guessDoor, prizeDoor):
if 1 != guessDoor and 1 != prizeDoor:
return 1
if 2 != guessDoor and 2 != prizeDoor:
return 2
return 3
def randomChoose(guessDoor, prizeDoor):
if guessDoor == 1:
return random.choice([2,3])
if guessDoor == 2:
return random.choice([1,3])
return random.choice([1,2])
def simMontyHall(numTrials, chooseFcn):
stickWins, switchWins, noWin = (0, 0, 0)
prizeDoorChoices = [1,2,3]
guessChoices = [1,2,3]
for t in range(numTrials):
prizeDoor = random.choice([1, 2, 3])
guess = random.choice([1, 2, 3])
toOpen = chooseFcn(guess, prizeDoor)
if toOpen == prizeDoor:
noWin += 1
elif guess == prizeDoor:
stickWins += 1
else:
switchWins += 1
return (stickWins, switchWins)
def displayMHSim(simResults, title):
stickWins, switchWins = simResults
pylab.pie([stickWins, switchWins],
colors = [‘r‘, ‘c‘],
labels = [‘stick‘, ‘change‘],
autopct = ‘%.2f%%‘)
pylab.title(title)
simResults = simMontyHall(100000, montyChoose)
displayMHSim(simResults, ‘Monty Chooses a Door‘)
pylab.figure()
simResults = simMontyHall(100000, randomChoose)
displayMHSim(simResults, ‘Door Chosen at Random‘)
pylab.show()
[3]
十分感谢,MIT的计算机编程导论公开课,他为我打开了新的一扇门
如果想更深入了解这个问题,或是想具体了解如何用计算机模拟其他的问题,可以阅读《编程导论》,那门公开课的教材最近被翻译成了中文。
决战21点,我最喜欢的电影之一,Micky教授就是通过这个问题,发现Ben在数学上面的天赋的。
(右键选择播放)
脑袋跟不上来哇,我希望你明白了我的解释。
参考资料:
[1-2] https://zh.wikipedia.org/wiki/%E8%92%99%E6%8F%90%E9%9C%8D%E7%88%BE%E5%95%8F%E9%A1%8C
[3] John V. Guttag. Introduction to Computation and Programming Using Python. The MIT Press. 2013.
标签:
原文地址:http://www.cnblogs.com/meelo/p/4447880.html