Decidability and Partial Decidability

标签：

1. Decidability

　　A predicate is decidable iff its characteristic function is computable, otherwise it is undecidable. An algorithm to compute the characteristic function of a decidable predicate is a decision procedure.

　　Theorem. Problem ‘x∈W_x‘ (i.e. Φ_x(x) is defined) is undecidable.

　　We prove that via the diagonal method: assume that x∈W_x is decidable, and then we can construct the following computable function, which is other than any computable (contradiction):

　　Corollary 1. There is a computable function h such that both ‘x∈Dom(x)‘ and ‘x∈Ran(h)‘ are undecidable.

　　　　　　e.g. h(x) = x ·1 (Ψ_U(x,x))

　　Corollary 2. (Halting Problem) Problem ‘Φ_x(y) is defined‘ is undecidable (whereas partailly decidable).

　　Corollary 3. Problem ‘Φ_x is 0‘ is undecidable. To prove it, we define f(x,y)= 0 (Ψ_U(x,x)), which is computable. According to the s-m-n theorem, there exists a total computable function K(x) such that Φ_K(x)(y) = f(x,y), and hence Φ_K(x) = 0 iff x∈W_x. If Φ_x = 0 is decidable, then Φ_K(x) = 0 is decidable and hence x∈W_x is decidable.

　　Corollary 4. Problem ‘Φ_x = Φ_y‘ is undecidable.

　　Corollary 5. Given any number c, the following problems are undecidable:

　　　　(1) (Acceptance Problem) c∈W_x;　　(2) (Printing Problem) c∈E_x.

　　　　Consider the following computable function and use the s-m-n theorem:

　　To prove a predicate about x is undecidable, we shall only to prove there exists a total computable function K(x) such that the predicate regarding K(x) is undecidable, and we construct the following computable function (g is a total computable function) to harness the s-m-n theorem:

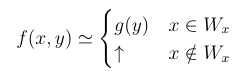
　　And thus we have

　　Having noted this, we have the following theorem:

　　Corollary 6. (Rice Theorem) For any non-empty proper subset of the unary function collection β, ‘Φ_x∈β‘ is undecidable.

2. Partial Decidability 　　

　　A predicate is partially decidable iff its partial characteristic function is computable. An algorithm to compute the partial characteristic function of a predicate is a partial decision procedure.

　　For instance, x∈W_x is partially decidable but x∉W_x is not partially decidable.

　　By definition, one should note that a predicate M(x) is partially decidable iff there is a computable function g(x) such that M(x) is equivalent to x∈Dom(g).

　　Theorem. Predicate M(x) is partially decidable iff there is a decidable predicate R(x,y) such that M(x) is equivalent to (∃y) R(x, y).

　　Theorem. If predicate M(x,y) is partially decidable, so is predicate (∃y) M(x, y).

　　Theorem. Predicate M(x) is decidable iff both M(x) and ¬M(x) are partially decidable.

　　　　Therefore, ‘P_x(y) is undefined‘ is not partially decidable, otherwise the halting problem is decidable.

　　Theorem. Let f(x) be a partial function, then f is computable iff the predicate ‘f(x)?y’ is partially decidable.

References:

　　1. Cutland, Nigel. Computability: an introduction to recursive function theory[M]. Cambridge: Cambridge University Press, 1980

Decidability and Partial Decidability

标签：

原文地址：http://www.cnblogs.com/DevinZ/p/4447538.html