uva 1533(bfs+状态压缩)

标签：uva   暴力   bfs   状态压缩   

题意：有一个棋盘如下，黑色表示有棋子，白色表示空，棋盘初始状态为有一个位置n为空，其他位置都有棋子。

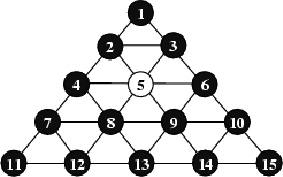
每次可以选择一个棋子在一条直线上隔一个或连续多个棋子跳到空白位置，然后这一个或多个棋子就被拿走，问最少几步可以使棋盘上的棋子拿走到只剩下一个且位置和初始空白位置相同。输出几步和每步的起始与落子位置。输出字典序最小的解，无解输出IMPOSSIBLE。

题解：因为棋盘上有15个位置，可以用状态压缩来表示棋盘的状态，1表示有棋子，0表示空白，每个棋子走的方向有6种，所以用一个flag[i][j]数组表示位置i走方向j的位置是什么，然后进行bfs，用异或操作更改棋盘状态。

#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
const int N = 15; 
int pos, mp[1 << N];
int flag[15][6] = {{-1,-1,-1,-1,2,3},{-1,1,-1,3,4,5},{1,-1,2,-1,5,6},
				 {-1,2,-1,5,7,8},{2,3,4,6,8,9},{3,-1,5,-1,9,10},
				 {-1,4,-1,8,11,12},{4,5,7,9,12,13},{5,6,8,10,13,14},
				 {6,-1,9,-1,14,15},{-1,7,-1,12,-1,-1},{7,8,11,13,-1,-1},
				 {8,9,12,14,-1,-1},{9,10,13,15,-1,-1},{10,-1,14,-1,-1,-1}};
struct P {
	int step;
	int	path[N + 5][2];
	int S;
	int num;
};

int bfs(int s) {
	queue<P> q;
	while (!q.empty())
		q.pop();
	P a;
	a.S = s;
	a.num = 1;
	a.step = 0;
	q.push(a);
	while (!q.empty()) {
		P u = q.front();
		q.pop();
		for (int i = 0; i < 15; i++) {
			if (u.S & (1 << i)) {
				for (int j = 0; j < 6; j++) {
					int cur = i;
					P b = u;
					if (flag[i][j] != -1 && b.S & (1 << (flag[i][j] - 1))) {
						while (cur != -1 && b.S & (1 << cur)) {
							b.S ^= (1 << cur);
							cur = flag[cur][j] - 1;
							b.num++;
						}
						if (cur < 0)
							continue;
						b.S |= (1 << cur);
						b.step = u.step + 1;
						b.path[b.step][0] = i;
						b.path[b.step][1] = cur;
						b.num--;
						if (!mp[b.S]) {
							if (b.num == 14 && b.S & (1 << (pos - 1))) {
								printf("%d\n%d %d", b.step, b.path[1][0] + 1, b.path[1][1] + 1);
								for (int k = 2; k <= b.step; k++)
									printf(" %d %d", b.path[k][0] + 1, b.path[k][1] + 1);
								printf("\n");
								return 1;
							}
							mp[b.S] = 1;
							q.push(b);
						}
					}
				}
			}
		}
	}
	return 0;
}

int main() {
	int t;
	scanf("%d", &t);
	while (t--) {
		scanf("%d", &pos);
		memset(mp, 0, sizeof(mp));
		int temp = ((1 << 15) - 1) ^ (1 << (pos - 1));
		mp[temp] = 1;
		int res = bfs(temp);
		if (!res)
			printf("IMPOSSIBLE\n");
	}
	return 0;
}

uva 1533(bfs+状态压缩)

标签：uva   暴力   bfs   状态压缩   

原文地址：http://blog.csdn.net/hyczms/article/details/45206861