标签:冲突的解决 hash函数 hash表的大小 hash学习
Hash表的出现主要是为了对内存中数据的快速、随机的访问。
它主要有三个关键点:Hash表的大小、Hash函数、冲突的解决。(hash表的实现)
1、Hash表的大小
Hash表的大小一般是定长的,如果太大,则浪费空间,如果太小,冲突发生的概率变大,体现不出效率。所以,选择合适的Hash表的大小是Hash表性能的关键。
对于Hash表大小的选择通常会考虑两点:
第一,确保Hash表的大小是一个素数。常识告诉我们,当除以一个素数时,会产生最分散的余数,可能最糟糕的除法是除以2的倍数,因为这只会屏蔽被除数中的位。由于我们通常使用表的大小对hash函数的结果进行模运算,如果表的大小是一个素数,就可以获得最佳的结果。
第二,创建大小合理的hash表。这就涉及到hash表的一个概念:装填因子。设装填因子为a,则:
a=表中记录数/hash表表长
通常,我们关注的是使hash表的平均查找长度最小,而平均查找长度是装填因子的函数,而不是表长n的函数。a的取值越小,产生冲突的机会就越小,但如果a取值过小,则会造成较大的空间浪费,通常,只要a的取值合适,hash表的平均查找长度就是一个常数,即hash表的平均查找长度为O(1)。
当然,根据不同的数据量,会有不同的哈希表的大小。对于数据量时多时少的应用,最好的设计是使用动态可变尺寸的哈希表,那么如果你发现哈希表尺寸太小了,比如其中的元素是哈希表尺寸的2倍时,我们就需要扩大哈希表尺寸,一般是扩大一倍。
下面是哈希表尺寸大小的可能取值:
17, 37, 79, 163, 331,
673, 1361, 2729, 5471, 10949,
21911, 43853, 87719, 175447, 350899,
701819, 1403641, 2807303, 5614657, 11229331,
22458671, 44917381, 89834777, 179669557, 359339171,
718678369, 1437356741, 2147483647
2、Hash函数
一个好的hash函数一般具有以下两个特点:
第一,速度快,
第二,能够将散列键均匀的分布在整个表中,保证不会产生聚集。
通常,hash函数具有如下形式:
hash-key = calculated-key % tablesize
上一节主要讨论了一下tablesize,为了提高散列键的离散程度,tablesize通常取素数。一般而言,没有绝对好的hash函数,hash函数的好坏很大程度上依赖于输入键的结构,人们讨论的最多的一般都是输入键为普通字符串的情况。这里也以字符串为例讨论如何一步步优化hash函数。
当键是字符串时,一种选择策略是简单的将字符串中每个字符的ASCII码加起来,代码如下:
unsigned int hash(const char *key, unsigned int tableSize)
{
unsigned int hashVal;
while(*key != ‘\0‘)
hashVal += *key++;
return (hashVal % tableSize);
}上面的hash函数实现简单而且能够很快的算出答案,不过,如果表很大,则函数就不能很好的分配键,例如,设tableSize=10949,并设所有的键至多8个字符长,由于ASCII字符的值最多是127,因此hash函数只能在0~1016之间取值,其中1016为127*8,显然这不是一种均匀的分配。
下面的hash函数对针对上面的缺点进行了改进。
unsigned int hash(const char *key, unsigned int tableSize)
{
return (key[0] + 27*key[1] + 729*key[2]) % tableSize;
}这个hash函数假设key至少有3个字符。值27表示英文字母表的字母个数外加一个空格,而729是27的平方。虽然该函数只考察了前三个字符,但是,假如字符出现的概率是随机的,而表的大小还是10949,那么我们就会得到一个合理的均衡分布。可是,英文不是随机的。虽然3个字符有 26*26*26=17567种可能的组合,但查验词汇量足够大的联机词典却揭示出:3个字母的不同组合数实际上只有2851种。即使这些组合没有冲突, 也不过只有表的28%被真正散列到。因此,虽然容易计算,但是当hash表足够大的时候,这个函数还是不合适。
针对以上缺点,进一步改进:
unsigned int hash(const char *key,unsigned int tableSize)
{
unsigned int hashVal;
while(*key != ‘\0‘)
hashVal = (hashVal << 5) + *key++;
return (hashVal % tableSize);
} 这个hash函数涉及键中的所有字符,并且一般可以分布的很好,它计算了字符串的如下值:

在计算该值时,利用了Horner法则,例如计算 hash=a+32b+32*32c 的另一种方式是借助公式:hash=((c)*32+b)*32+a。Horner法则将其扩展到用于n次多项式。该算法通过将乘法运算转换为位运算保证了hash函数快速的特点。
下面给出实际字符串hash应用中使用的很广的一个hash函数:ELFhash
unsigned long ELfHash(const unsigned char * key)
{
unsigned long h = 0, g;
while(*key)
{
h = (h << 4) + *key++;//把h左移4位加上该字符赋给h
if(g = h & 0xF0000000)//取h的高四位赋给g
h ^= g >> 24;//如果g不为0,让h和g的高八位异或再赋给h
h &= ~g;//对g取反并与h相与赋给h
}
return h;
}3、Hash冲突的解决
为提高hash表查找性能,除了考虑选择合适的hash表表长和完美的hash函数外,还必须考虑hash表处理冲突的能力。当hash函数对两个不同的数据项产生了相同的hash值时,冲突就产生了。对于冲突的处理,通常采用的方法可以分为三类:
(1)线性再散列法,简单的按顺序遍历hash表,寻找下一个可用的槽;
(2)非线性再散列法,计算一个新的hash值;
(3)外部拉链法,将hash表中的每个槽当作具有相同hash值的数据项所组成链表的头部,hash表将发生冲突的项添加到同一个链表中。
下面对这三种方法分别介绍。
线性再散列法是形式最简单的处理冲突的方法。插入元素时,如果发生冲突,算法会简单的遍历hash表,直到找到表中的下一个空槽,并将该元素放入该槽 中。查找元素时,首先散列值所指向的槽,如果没有找到匹配,则继续遍历hash表,直到:(1)找到相应的元素;(2)找到一个空槽(指示查找的元素不存 在);(3)整个hash表遍历完毕(指示该元素不存在并且hash表是满的)。下表显示了以线性再散列法将{89,18,49,58,69}5个元素插 入hash表的过程。(hash函数为:hash(X)=X mod 10;hash表长一般用素数,这里为了说明方便取表长为10)
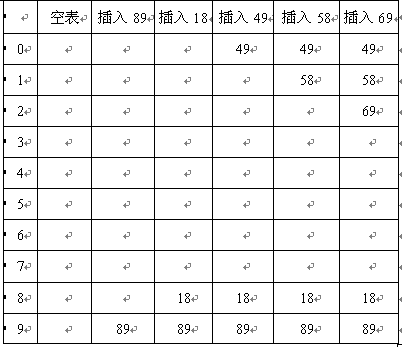
第一次冲突发生在插入关键字49时,它被放在下一个空闲地址,即地址0。关键字58依次和18,89,49发生冲突,试选三次之后才找到一个空单元。对
69的冲突用类似的方法处理。从以上过程可以看出,只要表中有空闲单元,总可以找到,但这里选择步长为1,将会在hash表中产生聚集,即:即使hash
表相对较空,还是会在某些区域形成一些区块,这些区块中的任何活动都将设计更大的步长。但如果以5或更大的值作为步长,可以迅速地从拥挤区域移开,从而减
少聚集现象的发生。事实上,只要hash表长和检查槽的步长是互质的,那么表中的每个槽都会被检查到。
线性再散列法有两个缺点:第一,不能从表中删除元素,因为相应的单元可能已经引起过冲突,元素绕过它存到了别处,例如,如果我们删除了18,那么其他的元素都会找不到。如果确实需要删除,可以采用懒惰删除的方法。第二,当表被填满时性能下降明显。
线性再散列法是从冲突位置开始,采用一个步长以顺序方式遍历hash表,来查找一个可用的槽,从上面的讨论可以看出,它容易产生聚集现象。非线性再散列法 可以避免遍历散列表,它会计算一个新的hash值,并通过它跳转到表中一个完全不同的部分。它的思想就是:通过跳转到表中不同的部分,从而避免相似值的聚 集,如果再散列函数跳转到的槽已经被占用了,则继续执行新一轮的再散列和跳转。
例如,还是上面的例子,如果再散列函数是hash(X)=R-(X mod R),其中R为小于hash表长的素数,如果我们选择R=7,则下表显示了插入与前面相同的关键字的结果。
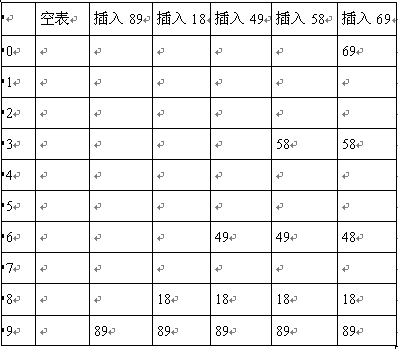
第一个冲突发生在49被插入的时候, hash(49)=7-0=7,故49被插入到位置6。Hash(58)=7-2=5,于是58被插入到位置3。最后69产生冲突,从而被插入到距离为hash(69)=7-6=1的地方。
非线性再散列法也有不能从表中删除元素的缺点。
无论是使用线性再散列法还是非线性再散列法,只有在散列表不会接近填满的情况下,才能使用再散列。当散列表的负载因子增大时,再散列所花费的时间也会显著增加。通过以上讨论可以看出,再散列方法适用于表负载较低并且不太可能执行删除操作的情况。
外部拉链法是将hash表看作是一个链表数组,表中的每个槽要不为空,要不指向hash到该槽的表项的链表。可以通过把元素添加到链表中来解决冲突。同 样,可以通过从链表中删除元素来执行删除操作。因此,解决冲突的代价不会超过向链表中添加一个节点,不需要执行再散列。在再散列中,表项的最大数量是由表 中槽的原始数量确定的,与之不同的是,外部拉链法可以容纳的元素于将在内存中存放的元素一样多。
外部拉链法的原则是:hash表的大小一般与预料的元素个数差不多。
假设有一个表长为10的hash表,给出10个关键字为前10个自然数的平方,hash函数为hash(X)=X mod 10,下图就是对应的外部拉链法的hash表。
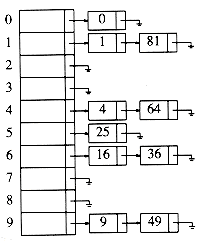
外部拉链法的平均查找时间是对链表的查找时间加上1,这个1是最初的定位hash表槽。外部拉链法的缺点是:它需要稍微多一些的空间来实现,因为添加任何 元素都需要添加指向节点的指针,并且每次探查也要花费稍微多一点的时间,因为它需要间接引用指针,而不是直接访问元素。由于今天的内存成本很低并且可以使 用非常快的CPU,所以这些缺点都是微不足道的。因此,实际使用hash表时,一般都是使用拉链法来解决hash冲突。
4、hash表的实现
由于实际应用中,拉链法实现hash表用的比较多,这里也以拉链法来实现hash表。
/*
* hashTable.h
*
* Created on: Nov 30, 2011
* Author: Liam Q
*/
#ifndef HASHTABLE_H_
#define HASHTABLE_H_
//定义DEBUG_MSG用于调试输出
#define DEBUG_MSG
//#define DEBUG_MSG(args) printf args; printf("\n");
typedef char * ElemType;//对字符串进行hash
typedef struct ListNode//链表中节点
{
ElemType elem;
struct ListNode * next;
}ListNode, *Position;
typedef Position List;//链表
typedef struct HashTbl//hash表
{
int tableSize;
List * theLists;
}HashTbl, *HashTable;
HashTable initTable(int tableSize);
void destroyTable(HashTable hashTable);
Position find(HashTable hashtable, ElemType elem);
void insert(HashTable hashTable, ElemType elem);
#endif /* HASHTABLE_H_ */
/*
* hashTable.c
*
* Created on: Nov 30, 2011
* Author: Liam Q
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include "hashTable.h"
#define MIN_TABLE_SIZE 10//hash表最小大小
static int isPrime(int a)
{
int i;
int b = (int)sqrt((double)a);
for(i = 2; i <= b; i++)
if(a % i == 0)
return 0;
return 1;
}
static int nextPrime(int a)
{
while(!isPrime(a++));
return --a;
}
HashTable initTable(int tableSize)
{
HashTable hashTable;
int i;
if(tableSize < MIN_TABLE_SIZE)
{
printf("Table size is too small\n");
return NULL;
}
hashTable = (HashTable)malloc(sizeof(HashTbl));
if(hashTable == NULL)
exit(-1);
hashTable->tableSize = nextPrime(tableSize);
hashTable->theLists = (List *)malloc(hashTable->tableSize * sizeof(List));
if(!hashTable->theLists)
exit(-1);
for(i = 0; i < hashTable->tableSize; i++)
{
hashTable->theLists[i] = (List)malloc(sizeof(ListNode));
if(!hashTable->theLists[i])
exit(-1);
else
hashTable->theLists[i]->next = NULL;
}
return hashTable;
}
void destroyTable(HashTable hashTable)
{
int i;
List l, tmp;
if(hashTable == NULL)
return;
if(hashTable->theLists)
{
for(i = 0; i < hashTable->tableSize; i++)
{
l = hashTable->theLists[i];
while(l != NULL)
{
tmp = l;
l = l->next;
free(tmp);
}
hashTable->theLists[i] = NULL;
}
free(hashTable->theLists);
}
free(hashTable);
}
static int hash(ElemType elem, int tableSize)
{
unsigned int hashVal = 0;
while(*elem != ‘\0‘)
hashVal = (hashVal << 5) + *elem++;
return hashVal % tableSize;
}
Position find(HashTable hashTable, ElemType elem)
{
Position p;
List l;
l = hashTable->theLists[hash(elem, hashTable->tableSize)];
p = l->next;
while(p != NULL && strcmp(p->elem, elem) != 0)
p = p->next;
return p;
}
void insert(HashTable hashTable, ElemType elem)
{
Position p, pNewCell;
List l;
p = find(hashTable, elem);
if(p == NULL)
{
pNewCell = (List)malloc(sizeof(ListNode));
if(pNewCell == NULL)
exit(-1);
else
{
l = hashTable->theLists[hash(elem, hashTable->tableSize)];
pNewCell->elem = (char *)malloc(strlen(elem) * sizeof(char));
strcpy(pNewCell->elem, elem);
pNewCell->next = l->next;
l->next = pNewCell;
DEBUG_MSG(("%d-----%s\n",hash(elem, hashTable->tableSize),pNewCell->elem));
}
}
}
/*
* demo.c .利用上面实现的hash表读取文本文件中单词,并将其放入hash表
*
* Created on: Nov 30, 2011
* Author: Liam Q
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "hashTable.h"
#define HASH_SIZE 500
#define MAXWORD 64
void createHashTable(HashTable hashTable)
{
char *fileName="Makefile.common";
FILE * fp;
char word[MAXWORD];
char c;
int i;
if((fp = fopen(fileName, "r")) == NULL)
{
fprintf(stderr,"can‘t open %s\n",fileName);
exit(-1);
}
c = ‘ ‘;
while(!feof(fp))
{
while(c != EOF && isspace(c))
c = fgetc(fp);
i = 0;
while(c != EOF && !isspace(c))
{
word[i++] = c;
c = fgetc(fp);
}
if(c == EOF)
break;
word[i] = ‘\0‘;
while(i >= 0 && ispunct(word[--i]))
word[i] = ‘\0‘;
insert(hashTable,word);
}
}
int main()
{
HashTable hashTable;
char word[MAXWORD];
hashTable = initTable(HASH_SIZE);
createHashTable(hashTable);
while(1)
{
printf("Search string:");
fgets(word, sizeof(word), stdin);
word[strlen(word) - 1] = ‘\0‘;
DEBUG_MSG(("%s",word));
printf("%s\n",find(hashTable,word)?"find":"not find");
}
destroyTable(hashTable);
hashTable = NULL;
}标签:冲突的解决 hash函数 hash表的大小 hash学习
原文地址:http://zlfwmm.blog.51cto.com/5892198/1637411