标签:
Description
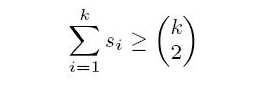
Input
Output
Sample Input
5 1 2 2 2 3 1 1 3 4 4 4 4 3 3 4 4 4 4 5 6 6 6 0 3 4 4 4 5 5 5 6 0 3 3 3 3 3
Sample Output
2 4 5 3 5
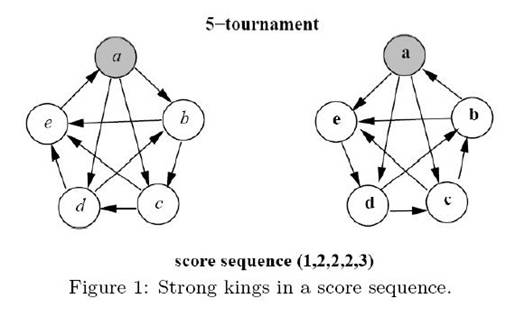
题目大意:有kase组数据。每组数据有一些人两两比赛,告诉你每个人赢得比赛的次数。如果一个人满足它打败了所有分数严格大于它的那个人,则它成为King;当然分数最高的人们自然也都是King。那么请问这场比赛最多能产生多少King呢?
分析:数据规模小的可怜,至多10组数据,每组数据至多10个人。首先明确一个贪心,就是King一定是比分最高的几个人,因为如果比分低的反而是King那么比分比它高的更容易成为King。然后注意的是不确定的输入我的处理办法是用stringstream提取一行即可。
然后我们用最大流的思路来解决。超级源点与所有选手相连,负载为胜利的次数。首先我们要去试探有几个King的时候满足条件,我采用的是二分,由于规模很小,枚举也行。然后在Kings确定了之后,对于每场比赛也看成一个节点,遍历两两选手i,j。如果i是King且score[j]>score[i],说明这场比赛i一定要赢,那么选手i与这场比赛连接,负载为1。如果不满足以上条件则说明此场胜负无所,选手i
、j 都与这场比赛连接,负载为1。最后再让每场比赛与超级汇点连接,负载为1。再跑最大流看看是否最大流=比赛总数n*(n-1)/2。根据结果二分。(枚举的话从低开始往高找,找到一组解即为最优解)。
上代码:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<sstream>
#include<string>
using namespace std;
const int MAXN = 210;
const int MAXM = 41000;
const int INF = 0x3f3f3f3f;
struct Edge
{
int from, to, cap, next;
};
Edge edge[MAXM];
int level[MAXN];
int head[MAXN];
int score[MAXN];
int bigger[MAXN];
int src, des, cnt;
void addedge( int from, int to, int cap )
{
edge[cnt].from = from;
edge[cnt].to = to;
edge[cnt].cap = cap;
edge[cnt].next = head[from];
head[from] = cnt++;
swap( from, to );
edge[cnt].from = from;
edge[cnt].to = to;
edge[cnt].cap = cap;
edge[cnt].next = head[from];
head[from] = cnt++;
}
int bfs()
{
memset( level, -1, sizeof level );
queue<int> q;
while (!q.empty())
q.pop();
level[src] = 0;
q.push( src );
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
if (edge[i].cap&&level[v] == -1)
{
level[v] = level[u] + 1;
q.push( v );
}
}
}
return level[des] != -1;
}
int dfs( int u, int f )
{
if (u == des) return f;
int tem;
for (int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
if (edge[i].cap&&level[v] == level[u] + 1)
{
tem = dfs( v, min( f, edge[i].cap ) );
if (tem > 0)
{
edge[i].cap -= tem;
edge[i ^ 1].cap += tem;
return tem;
}
}
}
level[u] = -1;
return 0;
}
int Dinic()
{
int ans = 0, tem;
while (bfs())
{
while (tem = dfs( src, INF ))
{
ans += tem;
}
}
return ans;
}
int main()
{
int kase;
cin >> kase;
getchar();
src = 0; des = 105;
while (kase--)
{
int n = 0;
string str;
getline( cin, str );
stringstream ss( str );
int sc;
while (ss >> sc)
{
score[++n] = sc;
}
bigger[n] = 0;
for (int i = n - 1; i >= 1; i--)
{
if (score[i] == score[i + 1]) bigger[i] = bigger[i + 1];
else bigger[i] = n - i;
}
int start;
for ( start = 1; start <= n; start++)
{
if (score[start] >= bigger[start])break;
}
int low = start, high = n;
int ans = start;
while(low<=high)
{
int mid = (low + high) / 2;
memset( head, -1, sizeof head );
cnt = 0;
int match = 0;
for (int i = 1; i <= n; i++)
{
addedge( src, i, score[i] );
}
for (int i = 1; i <= n; i++)
{
for (int j = i+1; j <= n; j++)
{
if (i >= mid&&score[j] > score[i])
addedge( i, (++match) + 50, 1 );
else
{
addedge( i, (++match) + 50, 1 );
addedge( j, match + 50, 1 );
}
}
}
for (int i = 1; i <= match; i++)
{
addedge( i + 50, des, 1 );
}
if (Dinic() < (n*(n-1))/2) low = mid + 1;
else
{
ans = mid;
high = mid - 1;
}
}
cout << n - ans + 1 << endl;
}
return 0;
}
解题报告 之 POJ2699 The Maximum Number of Strong Kings
标签:
原文地址:http://blog.csdn.net/maxichu/article/details/45269497