标签:
1 什么是协同过滤
协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤 (Collaborative Filtering, 简称 CF),首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。
换句话说,就是借鉴和你相关人群的观点来进行推荐,很好理解。
2 协同过滤的实现
要实现协同过滤的推荐算法,要进行以下三个步骤:
收集数据——找到相似用户和物品——进行推荐
3.收集数据
这里的数据指的都是用户的历史行为数据,比如用户的购买历史,关注,收藏行为,或者发表了某些评论,给某个物品打了多少分等等,这些都可以用来作为数据供推荐算法使用,服务于推荐算法。需要特别指出的在于,不同的数据准确性不同,粒度也不同,在使用时需要考虑到噪音所带来的影响。
4.找到相似用户和物品
这一步也很简单,其实就是计算用户间以及物品间的相似度。以下是几种计算相似度的方法(可以在Mahout的taste里的几种相似度计算方法):
最初用于计算欧几里德空间中两个点的距离,以两个用户x和y为例子,看成是n维空间的两个向量x和y, xi表示用户x对itemi的喜好值,yi表示用户y对itemi的喜好值,他们之前的欧几里德距离是
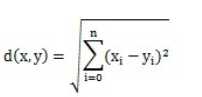
对应的欧几里德相似度,一般采用以下公式进行转换:距离越小 ,相似度越大
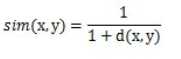
在taste里,计算user之间和item之前欧几里德相似度的类是EuclideanDistanceSimilarity。
皮尔逊相关系数一般用于计算两个定距变量间线性相关的紧密程度,它的取值在[-1,+1]之间。当取值大于0时表示两个变量是正相关的,即一个变量的值越大,另一个变量的值也会越大;当取值小于0时表示两个变量是负相关的,即一个变量的值越大,另一个变量的值反而会越小。其计算公式如下
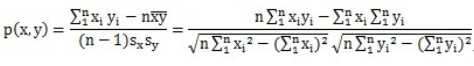
其中sx和sy是样品的标准偏差
在taste里, PearsonCorrelationSimilarity的实现方式不是采用上述公式,而是采用3的实现。
就是两个向量的夹角余弦,被广泛应用于计算文档数据的相似度
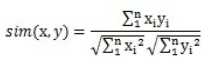
在taste里, 实现Cosine相似度的类是PearsonCorrelationSimilarity, 另外一个类UncenteredCosineSimilarity的实现了形式化以后的cosine向量夹角,如下公式
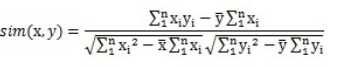
用这种公式计算的原因如下:余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感。因此没法衡量每个维数值的差异,会导致这样一个情况:比如用户对内容评分,5分制,X和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得出的结果是0.98,两者极为相似,但从评分上看X似乎不喜欢这2个内容,而Y比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性,就出现了调整余弦相似度,即所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
Tanimoto系数也称Jaccard系数,是Cosine相似度的扩展,也多用于计算文档相似度。计算公式如下:
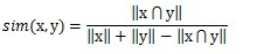
其中x表示用户x所喜好的所有item的集合, y表示用户y所喜好的所有item的集合。
在taste里,实现Tanimoto 相似度的类是TanimotoCoefficientSimilarity,可以看出这种计算方法适用于用户对item的喜好是0和1那种情况。
出租车几何或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ,是种使用在几何度量空间的几何学用语,用以标明两个点上在标准坐标系上的绝对轴距总和。图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
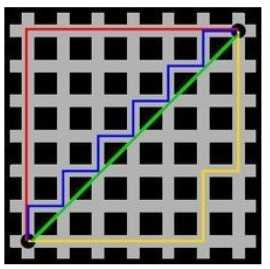
计算公式是:
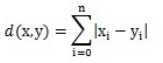
转换后的相似度为:
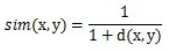
在tasete里的实现类CityBlockSimilarity采用了简化的计算方式,比较适用于用户的喜欢数据时0或者1的情况
公式比较复杂,实现类为LogLikelihoodSimilarity,比较适用于用户的喜欢数据时0或者1的情况
斯皮尔曼相关性可以理解为是排列后(Rank)用户喜好值之间的Pearson相关度。《Mahout in Action》中有这样的解释:假设对于每个用户,我们找到他最不喜欢的物品,重写他的评分值为“1”;然后找到下一个最不喜欢的物品,重写评分值为“2”,依此类推。然后我们对这些转换后的值求Pearson相关系数,这就是Spearman相关系数。
斯皮尔曼相关度的计算舍弃了一些重要信息,即真实的评分值。但它保留了用户喜好值的本质特性——排序(ordering),它是建立在排序(或等级,Rank)的基础上计算的。
因为斯皮尔曼相关性的计算需要花时间计算并存储喜好值的一个排序(Ranks),具体时间取决于数据的数量级大小。正因为这样,斯皮尔曼相关系数一般用于学术研究或者是小规模的计算。
在taste里的实现类为SpearmanCorrelationSimilarity
5.进行推荐
在知道了如何计算相似度后,就可以进行推荐了。
在协同过滤中,有两种主流方法:基于用户的协同过滤,和基于物品的协同过滤。具体怎么来阐述他们的原理呢,看个图大家就明白了
基于用户的 CF 的基本思想相当简单,基于用户对物品的偏好找到相邻邻居用户,然后将邻居用户喜欢的推荐给当前用户。计算上,就是将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,找到 K 邻居后,根据邻居的相似度权重以及他们对物品的偏好,预测当前用户没有偏好的未涉及物品,计算得到一个排序的物品列表作为推荐。 下图给出了一个例子,对于用户 A,根据用户的历史偏好,这里只计算得到一个邻居 - 用户 C,然后将用户 C 喜欢的物品 D 推荐给用户 A。

基于物品的 CF 的原理和基于用户的 CF 类似,只是在计算邻居时采用物品本身,而不是从用户的角度,即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。从计算的角度看,就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度,得到物品的相似物品后,根据用户历史的偏好预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。下图给出了一个例子,对于物品 A,根据所有用户的历史偏好,喜欢物品 A 的用户都喜欢物品 C,得出物品 A 和物品 C 比较相似,而用户 C 喜欢物品 A,那么可以推断出用户 C 可能也喜欢物品 C。

6.举个例子来说明:
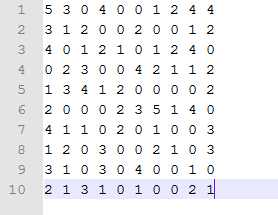
上面每一行代表一个用户,每一列代表一个商品,比如第2行第一列的3表示用户2对商品1的评分为3,0代表对应的用户还没有购买过该商品,现在想预测用户2对商品4的评分:
要计算用户2与用户1之间的相似度,首先找到二者都评过分的商品为:商品1, 2, 9, 10,用户1对这4个商品的评分向量为r1=[5 3 4 4],用户2对这4个商品评分向量为r2=[3 1 1 2];所谓余弦相似度就是利用两个向量之间夹角的余弦值来衡量两个向量之间的相似度,显然夹角越小,余弦值就越大,两个向量就越靠近,即二者越相似,于是用户2和用户1之间的相似度就为sim2_1=(5*3 + 3*1 + 4*1 + 4*2)/ (||r1|| * ||r2||) = 0.953, 其中||r||代表向量r的模长或者2范数,类似地分别计算出用户2与用户3 5 8 9 10之间的sim2_3,sim2_5,sim2_8,sim2_9,sim2_10
package pku;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Recommendation {
public static final int KNEIGHBOUR = 3;
public static final int COLUMNCOUNT = 8; //number of items
public static final int PREFROWCOUNT = 20;
public static final int TESTROWCOUNT = 5;
private String[] bookName = {"数据挖掘:概念与技术","金融工程","投资银行学","算法导论","machine learning","经济学原理","金融的逻辑","Thinking in Java"};
public void generateRecommendations() {
int[][] preference = readFile(PREFROWCOUNT, "preference.data");
int[][] test = readFile(TESTROWCOUNT, "test.data");
double[][] similarityMatrix = produceSimilarityMatrix(preference);
// for (int i = 0; i < similarityMatrix.length; i++) {
// for (int j = 0; j < similarityMatrix[0].length; j++) {
// System.out.print(similarityMatrix[i][j]+" ");
// }
// System.out.println();
// }
List<Integer> neighborSerial = new ArrayList<Integer>();
for (int i = 0; i < TESTROWCOUNT; i++) {
neighborSerial.clear();
double max = 0;
int itemSerial = 0;
for (int j = 0; j < COLUMNCOUNT; j++) {
if(test[i][j] == 0) {
double similaritySum = 0;
double sum = 0;
double score = 0;
neighborSerial = findKNeighbors(test[i], j, similarityMatrix);
for (int m = 0; m < neighborSerial.size(); m++) {
sum += similarityMatrix[j][neighborSerial.get(m)] * test[i][neighborSerial.get(m)];
similaritySum += similarityMatrix[j][neighborSerial.get(m)];
}
score = sum / similaritySum;
if(score > max) {
max = score;
itemSerial = j;
}
}
}
System.out.println("The book recommended for user "+i+" is: "+bookName[itemSerial]+" score: "+max);
}
}
/**
* This method is used to find the nearest K neighbors to the un_scored item
* @param score
* @param i
* @param similarityMatrix
* @return
*/
private List<Integer> findKNeighbors(int[] score,int i,double[][] similarityMatrix) { //该方法有三个参数,score表示某一用户对所有项目的评分;i表示某个项目的序号
List<Integer> neighborSerial = new ArrayList<Integer>();
double[] similarity = new double[similarityMatrix.length];
for (int j = 0; j < similarityMatrix.length; j++) {
if(score[j] != 0) {
similarity[j] = similarityMatrix[j][i];
}
else {
similarity[j] = 0;
}
}
double[] temp = new double[similarity.length];
for (int j = 0; j < temp.length; j++) {
temp[j] = similarity[j];
}
Arrays.sort(temp);
for(int j = 0; j < similarity.length; j++) {
for (int m = temp.length - 1; m >= temp.length - KNEIGHBOUR; m--) {
if (similarity[j] == temp[m] && similarity[j] != 0.0)
neighborSerial.add(new Integer(j));
}
}
return neighborSerial;
}
/**
* This method is used to produce similarity matrix among items
* @param preference
* @return
*/
private double[][] produceSimilarityMatrix(int[][] preference) {
double[][] similarityMatrix = new double[COLUMNCOUNT][COLUMNCOUNT];
for (int i = 0; i < COLUMNCOUNT; i++) {
for (int j = 0; j < COLUMNCOUNT; j++) {
if (i == j) {
similarityMatrix[i][j] = 0;
}
else {
similarityMatrix[i][j] = computeSimilarity(preference[i], preference[j]);
}
}
}
// for (int i = 0; i < similarityMatrix.length; i++) {
// for (int j = 0; j < similarityMatrix[0].length; j++) {
// System.out.print(similarityMatrix[i][j]);
// }
// System.out.println();
// }
// System.out.println("**********");
return similarityMatrix;
}
/**
* This method is used to compute similarity between two items
* @param item1
* @param item2
* @return
*/
private double computeSimilarity(int[] item1,int[] item2) {
List<Integer> list1 = new ArrayList<Integer>();
List<Integer> list2 = new ArrayList<Integer>();
int j = 0;
for (int i = 0; i < item1.length; i++) {
if(item1[i] != 0 && item2[i] !=0) {
list1.add(new Integer(item1[i]));
list2.add(new Integer(item2[i]));
}
j++;
}
return pearsonCorrelation(list1,list2);
}
/**
* This method is used to read file and store file data into arrays
* @param rowCount
* @param fileName
* @return
*/
private int[][] readFile(int rowCount,String fileName) {
int[][] preference = new int[rowCount][COLUMNCOUNT];
try {
File file = new File(fileName);
FileReader fr = new FileReader(file);
BufferedReader br = new BufferedReader(fr);
String line = "";
int i = 0;
while (br.ready()) {
line = br.readLine();
String[] data = line.split(",");
for (int j = 0; j < data.length; j++) {
preference[i][j] = Integer.parseInt(data[j]);
}
i++;
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
return preference;
}
/**
* This method is used to compute Pearson Correlation between two items
* @param a
* @param b
* @return
*/
private double pearsonCorrelation(List<Integer> a,List<Integer> b) {
int num = a.size();
int sum_prefOne = 0;
int sum_prefTwo = 0;
int sum_squareOne = 0;
int sum_squareTwo = 0;
int sum_product = 0;
for (int i = 0; i < num; i++) {
sum_prefOne += a.get(i);
sum_prefTwo += b.get(i);
sum_squareOne += Math.pow(a.get(i), 2);
sum_squareTwo += Math.pow(b.get(i), 2);
sum_product += a.get(i) * b.get(i);
}
double sum = num * sum_product - sum_prefOne * sum_prefTwo;
double den = Math.sqrt((num * sum_squareOne - Math.pow(sum_squareOne, 2)) * (num * sum_squareTwo - Math.pow(sum_squareTwo, 2)));
double result = sum / den;
return result;
}
public static void main (String[] args) {
Recommendation application = new Recommendation();
application.generateRecommendations();
}
}
标签:
原文地址:http://www.cnblogs.com/yangxiao99/p/4456038.html