数据分类

标签：

1定义

• 是指把数据样本映射到一个事先定义的类中的学习过程；即给定一组输入的属性向量及其对应的类，用基于归纳的学习算法得出分类
• 所以数据分类的任务：通过学习得到一个目标函数f，把每个属性集x映射到一个预先定义的类标号y；

2示例

　　数据集包含多个描述属性和一个类别属性，一般来数，描述属性：连续值或离散值；类别属性：只能是离散值（目标属性连续对应回归问题）

　　两类分类示例

• 银行业：区分高端信用卡和低端信用卡
• 医疗诊断：区分正常细胞和癌细胞
• 互联网：区分正常邮件和垃圾邮件

　　多类分类示例

• 油气传输：区分行人走过、汽车碾过、镐刨、电钻等行为
• 文字识别：区分不同的字符（其中汉字识别是一个大类别问题）
• 社会网络：区分中心用户、活跃用户、不活跃用户、马甲用户等

3分类过程

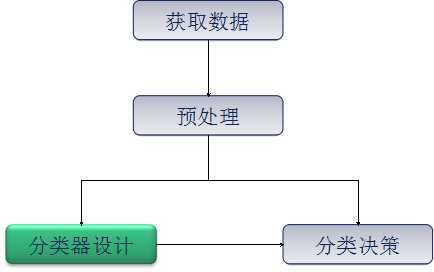
3.1获取数据

　　数值型数据

• 病例中的各种化验数据
• 空气质量监测数据

　　描述性数据

• 人事部门档案资料

　　图片型数据

• 指纹、掌纹
• 自然场景图片

　　很多情况下，需要将上述数据统一转换为数值型数据序列，即形成特征向量（特征提取）

3.2预处理

　　为了提高分类的准确性和有效性，需要对分类所用的数据进行预处理

• 去除噪声数据
• 对空缺值进行处理
• 数据降维（特征选择）--（PCA、LDA）

　　备注：主成分分析 （ Principal Component Analysis ， PCA ）

　　　　　线性鉴别分析(Linear Discriminant Analysis, LDA)，也称Fisher线性判别(Fisher Linear Discriminant ,FLD)， 这种算法是Ronald Fisher 于 1936年发明的，是模式识别的经典算法。

3.3分类器设计

3.3.1划分数据集

　　给定带有类标号的数据集，并且将数据集划分为两个部分

• 训练集（training set）
• 测试集（testing set）

　　划分策略：

　　1.当数据集D的规模较大时

　　　　训练集2|D|/3，测试集是1|D|/3

　　2.当数据集D的规模不大时

　　　　n交叉验证法（n-fold validation） 将数据集随机地划分为n组 之后执行n次循环，在第i次循环中，将第i组数据样本作为测试集，其余的n-1组数据样本作为训练集,最终的精度为n个精度的平均值。

　　3.当数据集D的规模非常小时　　

　　　　每次交叉验证时，只选择一条测试数据，剩余的数据均作为训练集。 原始数据集有m条数据时，相当于m-次交叉验证。 是N-次交叉验证的一个特例。

3.3.2分类器构造　　

　　利用训练集构造分类器（分类模型）

　　通过分析由属性描述的每类样本的数据信息，从中总结出分类的规律性，建立判别公式或判别规则

　　在分类器构造过程中，由于提供了每个训练样本的类标号，这一步也称作监督学习（supervised learning）

3.3.3分类器测试

　　利用测试集对分类器的分类性能进行评估，具体方式是：

　　首先，利用分类器对测试集中的每一个样本进行分类

　　其次，将分类得到的类标号和测试集中数据样本的原始类标号进行对比

　　由上述过程得到分类器的分类性能（如何评价？）

　　分类的评价准则---约定和假设

　　1）指标一，精确度（accuracy）　　

• 是最常用的评价准则
• 代表测试集中被正确分类的数据样本所占的比例
• 反映了分类器对于数据集的整体分类性能  

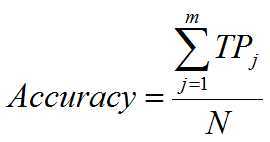
　　 1）指标一，精确度（accuracy）

3.4分类决策

　　在构造成功分类器之后（通过测试），则可以利用该分类器实际执行分类。

数据分类

标签：

原文地址：http://www.cnblogs.com/chamie/p/4457093.html