LeetCode: JumpGame 1 and 2

标签：

Title :

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

For example:
A = [2,3,1,1,4], return true.

A = [3,2,1,0,4], return false.

思路：

使用贪心算法，用maxStep来记录当前位置跳的最远距离，更新maxStep = max(A[i],maxStep),每前进一步，maxStep--

class Solution {
public:
    bool canJump(int A[], int n) {
        if (n == 0 || n == 1)
            return true;
        int maxStep = A[0];
        for (int i = 1 ; i < n ; i++){
            if (0 == maxStep)
                return false;
            maxStep--;
            maxStep = max(maxStep,A[i]);
            if (i + maxStep >= n-1)
                return true;
        }
    }
};

Jump Game2

Title

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Your goal is to reach the last index in the minimum number of jumps.

For example:
Given array A = [2,3,1,1,4]

The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)

思路1 : 使用动态规划来做，不过超时

int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int> result(n,INT_MAX);
        result[0] = 0;
        for (int i = 0 ; i < nums.size(); i++){
            for (int j = i+1; j <= i+ nums[i]; j++){
                if (j  >= nums.size())
                    break;
                result[j] = min(result[j],result[i]+1);
            }
        }
        return result[n-1];
    }

思路2 ： 大牛写的扫描一遍。我仔细想了想，扫描一遍和动态规划有些相似之处。在动态规划中，我们需要对每个i更新下在他的jump范围内的其他点的跳数。那么扫面一遍的思路呢，是用两个变量last，cur来记录，last是记录之前的step下能跳的最远距离，cur则是记录下当前能到达的最远距离。更新last是在当前的i超过了last，则说明已经突破之前的势力范围，需要更新，用

http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html 中的例子来说明

比如就是我们题目中的[2,3,1,1,4]。初始状态是这样的：cur表示最远能覆盖到的地方，用红色表示。last表示已经覆盖的地方，用箭头表示。它们都指在第一个元素上。

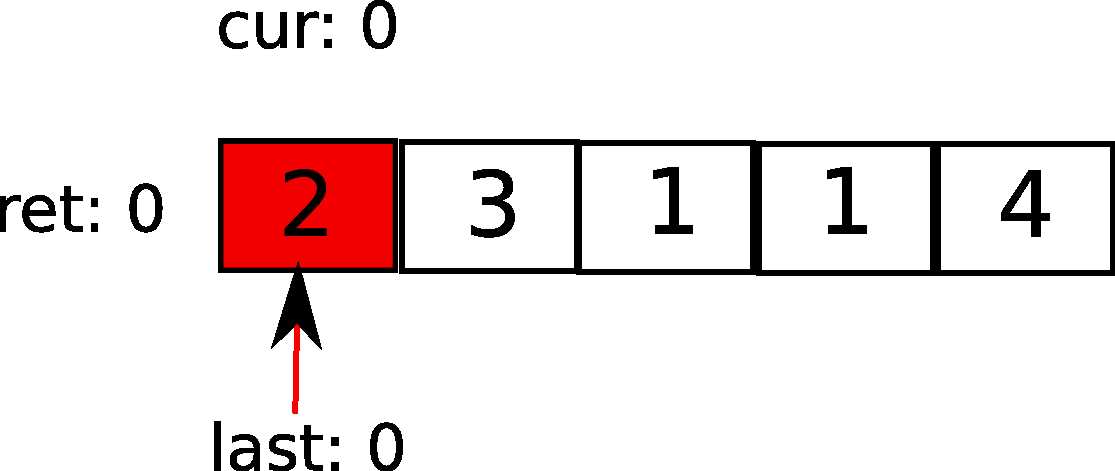
接下来，第一元素告诉cur，最远咱可以走2步。于是：

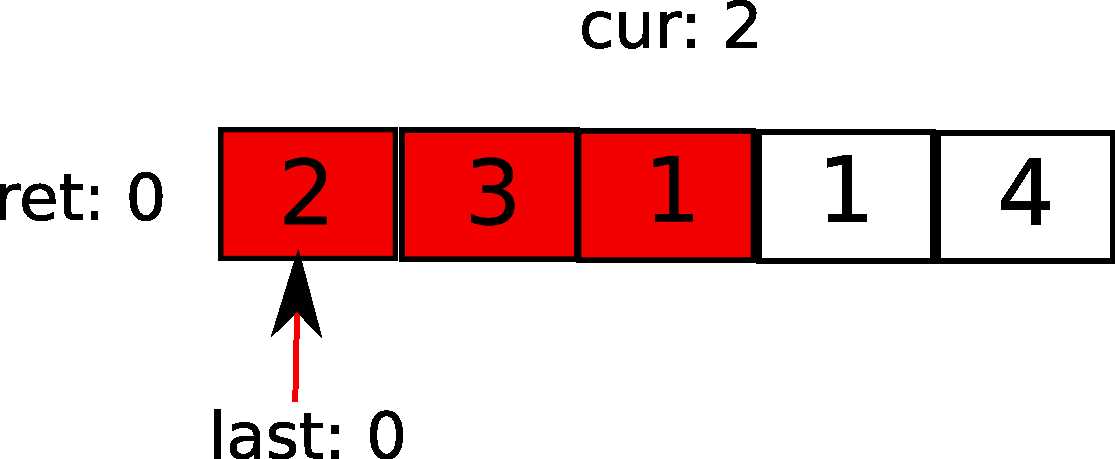
下一循环中，i指向1（图中的元素3），发现，哦，i小于last能到的范围，于是更新last（相当于说，进入了新的势力范围），步数ret加1.同时要更新cur。因为最远距离发现了。

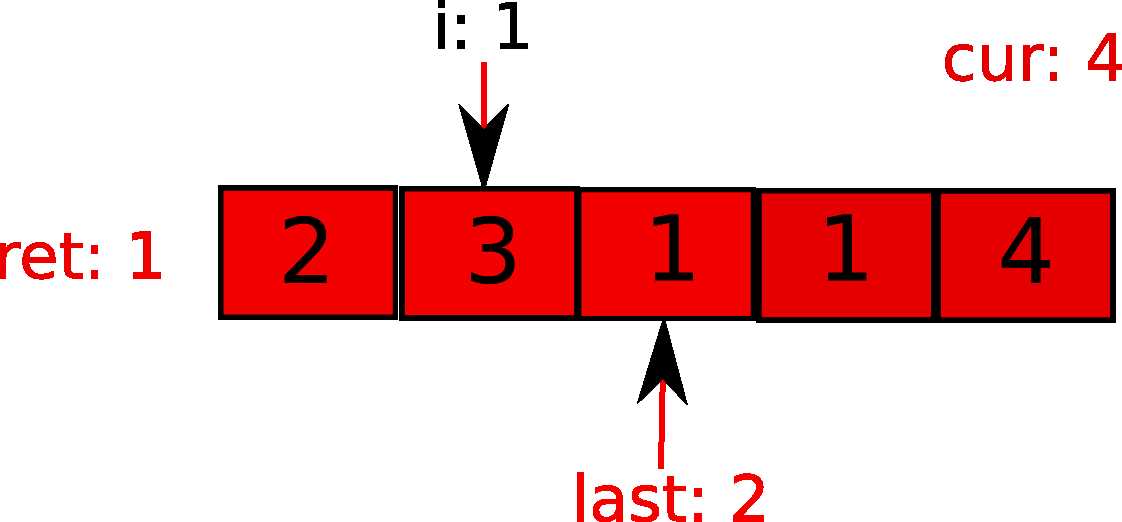
接下来，i继续前进，发现i在当前的势力范围内，无需更新last和步数ret。更新cur。

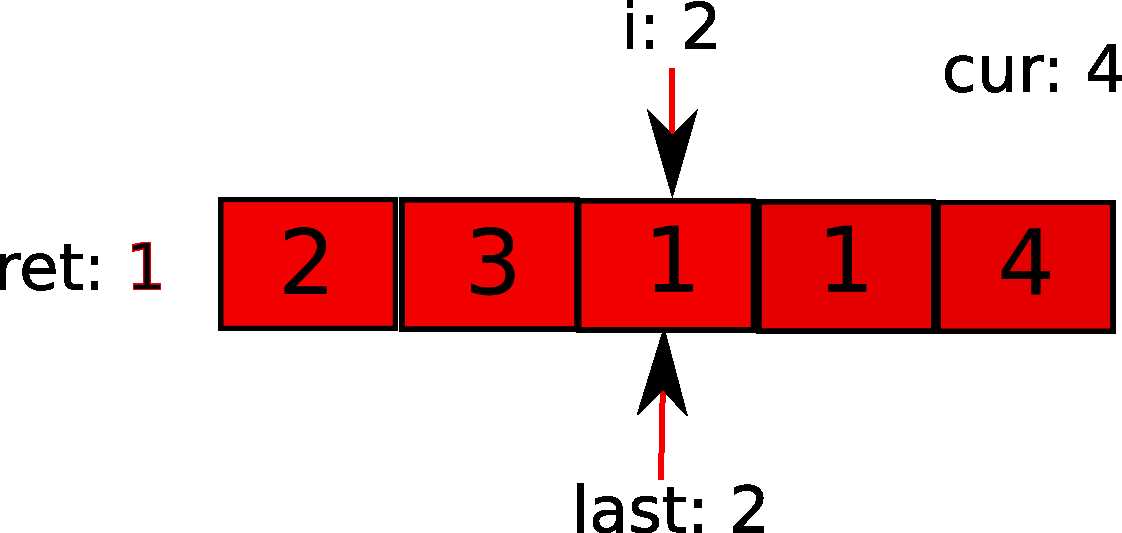
i继续前进，接下来发现超过当前势力范围，更新last和步数。cur已然最大了。

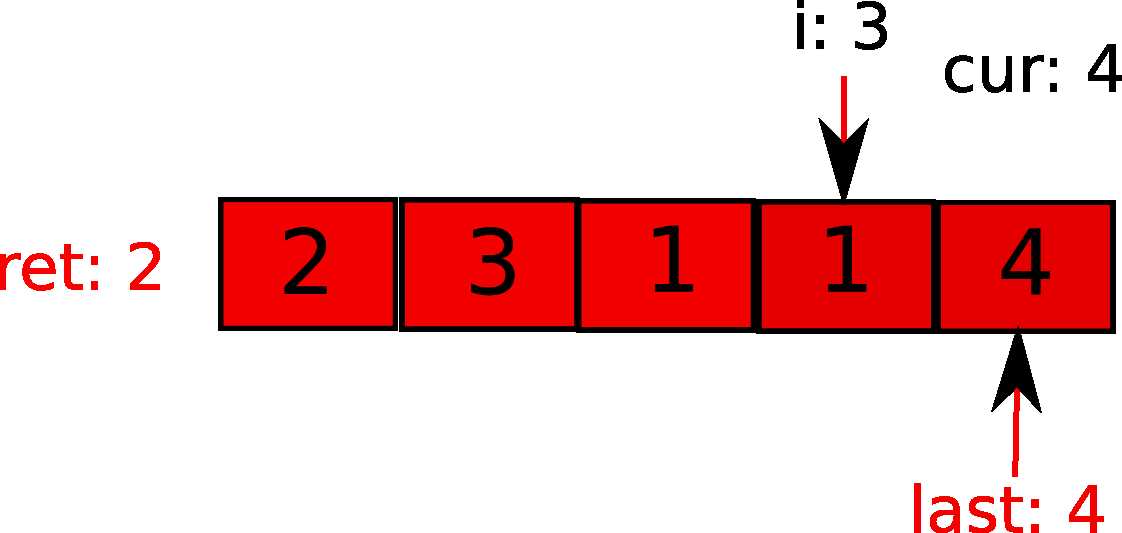
最后，i到最后一个元素。依然在势力范围内，遍历完成，返回ret。

/*
 * We use "last" to keep track of the maximum distance that has been reached
 * by using the minimum steps "ret", whereas "curr" is the maximum distance
 * that can be reached by using "ret+1" steps. Thus,
 * curr = max(i+A[i]) where 0 <= i <= last.
 */
class Solution {
public:
    int jump(int A[], int n) {
        int ret = 0;
        int last = 0;
        int curr = 0;
        for (int i = 0; i < n; ++i) {
            if (i > last) {
                last = curr;
                ++ret;
            }
            curr = max(curr, i+A[i]);
        }

        return ret;
    }
};

LeetCode: JumpGame 1 and 2

标签：

原文地址：http://www.cnblogs.com/yxzfscg/p/4457367.html