频率分布分析:
频率分布主要用直方图进行分析(连续数据,离散数据使用散点图),直方图是一种显示数据分布情况的柱形图,即不同数据出现的频率。通过这些高度不同的柱形,可以直观、快速地观察数据的分散程度和中心趋势。
直方图适用于连续数据的分析,因此对数据量有一定的要求。如果数据量很少时,可以直接使用散点图进行展示。
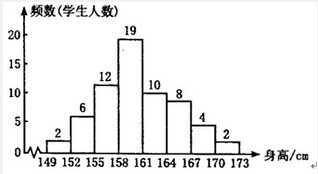
上图:数据是否正态分布
上图:数据左倾还是右倾
上图:数据是否围绕某个值紧密聚集
上图:数据是否位于设定的限制中
相关性及数据分布分析:
对于相关性及数据分布分析,我们一般使用散点图进行分析。散点图是用来判断两个变量之间的相互关系的工具,一般情况下,散点图用两组数据构成多个坐标点,通过观察坐标点的分布,判断变量间是否存在关联关系,以及相关关系的强度。如果不存在相关关系,可以使用散点图总结特征点的分布模式,即矩阵图(象限图)。
1、相关关系分析
需要注意的是,相关关系不同于因果关系,相关性表示两个变量同时变化,而因果关系是一个变量导致另一个变量变化。散点图只是一种数据的初步分析工具,能够直观的观察两组数据间可能存在什么关系,在分析的时候如果找到变量间可能存在的关系,则需要进一步确认是否存在因果关系,使用更多的统计分析工具进行分析。
进行相关关系分析时的时候,应该使用连续数据,一般在X轴(横轴)上放置自变量,Y轴(纵轴)上放置因变量,在坐标系上绘制出相应的点。散点图的形状可能表现为变量间的线性关系、指数关系或对数关系等,以线性关系为例,散点图一般会包括如下几种典型形状。
·正相关 :自变量为X变大的时候,因变量Y随之变大。
·负相关:自变量X变大的时候,因变量Y随之变小。
·不相关:因变量Y不随自变量X的变化而变化。
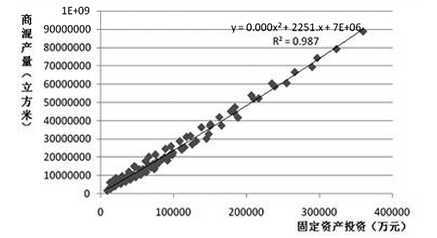
上图:正相关
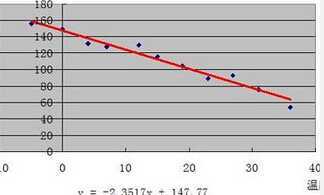
上图:负相关
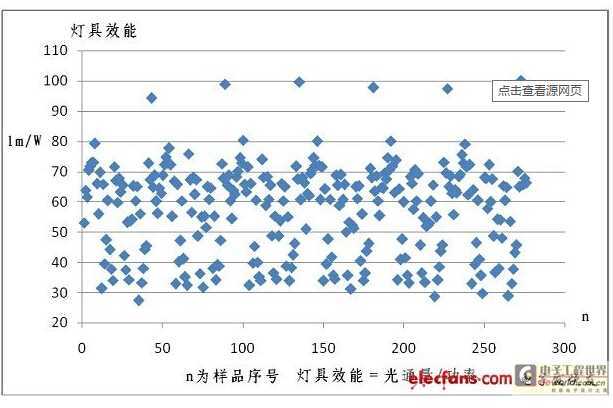
上图:不相关
2、矩阵分析
矩阵分析分为二维矩阵,和多维矩阵,二维就是两个可以数据化的标尺的考量,适用于于数据比较少的连续数据,和不可连续的离散数据。一般用于查看集中程度,和筛选限定条件的数据。它也是数据表达最灵活的方式之一。
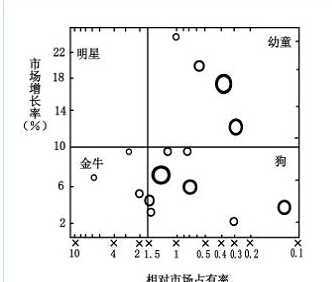
差异分析
差异分析也就是对比分析,就是将两个或两个以上的数据进行比较,分析它们之间的差异,从而揭示这些数据所代表的发展变化情况和规律。通过对比,可以很直观看出事物在某方面的差距,并且可以准确、量化地表示出差距的多少。
对比的分类
根据对比的对象和方式,可以将其区分为横向和纵向比较。
横向比较是指在同一时间条件下,对不同总体指标的比较,例如华南、华中、华北等的销售业绩比较。
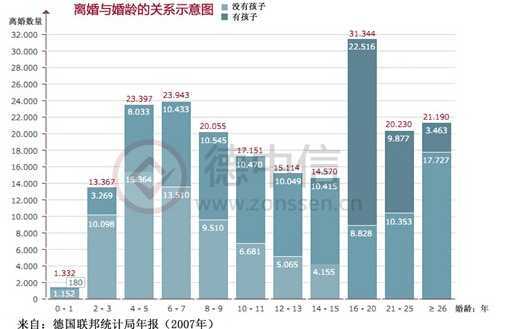
上图:横向比较
纵向比较就是指在同一总体条件下,对不同时期指标数据的比较。例如,与上季度比较、与上年同期比较、与活动前比较、与计划比较。
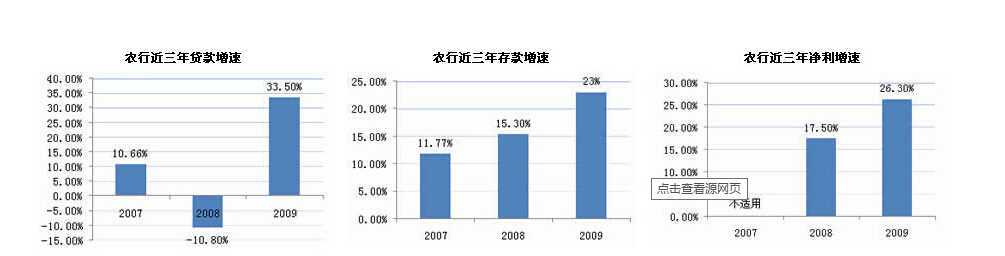
上图:纵向比较
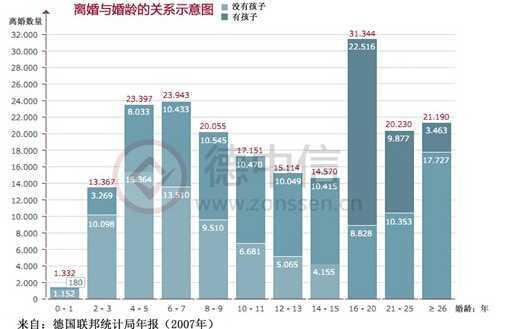
上图:堆积图横向对比
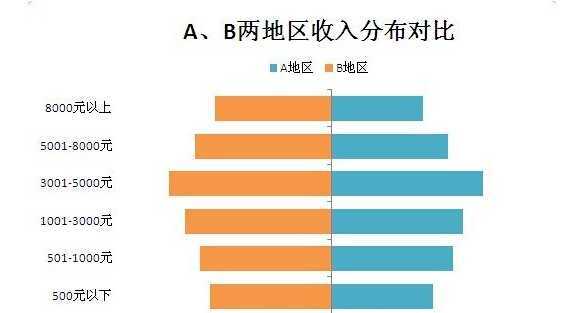
上图:对称条形图,用于两组数据的多个维度对比
对比分析的注意事项。
指标的口径范围、计算方法、计量单位必须一致。
对比的对象要具有可比性。
对比的指标类型必须一致。无论绝对数指标、相对数指标、平均数指标,还是其他类型的指标,在进行对比时双方必须同一,长度与宽度是无法进行比较的。
___________________________________________________________________
写字不易,且读且珍惜,转载请注明出处:SimonK @http://www.cnblogs.com/simonk/
更博时间:
周一到周五每天一更,时间22:00-23:40之间
周六/周日/法定节假日 不定期
欢迎订阅!
下节预报:简单图表分析之算数平均分析、趋势分析、漏斗分析
___________________________________________________________________
原文地址:http://www.cnblogs.com/simonk/p/3778941.html